【大宇宙小故事】29 勾除昨日與明朝

撰文｜葉李華

　　一簞疏食一壺漿

　　一卷詩書樹下涼

　　卿為阿儂歌瀚海

　　茫茫瀚海即天堂

──《魯拜集》第12首‧黃克孫譯

在世人心目中，最有名的伊斯蘭文學作品當然是《天方夜譚》，其次大概就是由101首波斯四行詩組成的《魯拜集》。這本詩集之所以成為世界名著，主要是因為在十九世紀就出現了英譯本，譯者是英國詩人費茲哲羅(Edward FitzGerald)。而在中文世界，《魯拜集》雖然名氣較小，仍有許多各具特色的譯本，包括華裔物理學家黃克孫的七言絕句版。

黃氏的譯本特別註明是「衍譯」，也就是強調不力求忠於原著。事實上，費茲哲羅的英譯也常有自由發揮之處，黃老師只是延續這個傳統罷了。正因為如此，下面這首詩雖然頗具朦朧美感，恐怕無法從字裡行間看出背後的典故。

　　曾司北斗與招搖

　　玉曆天衡略整調

　　紙上淋漓縱醉筆

　　勾除昨日與明朝

──《魯拜集》第57首‧黃克孫譯

讓我們看看另一個非常忠於英譯的版本(郭沫若1924)是怎麼寫的。

　　啊，人們說我的推算高明(Ah, but my Computations, People say,)

　　我曾經把舊曆的歲時改正(Reduc'd the Year to better reckoning?--Nay,)

　　誰知道那只是從曆書之中('Twas only striking from the Calendar)

　　消去未生的明日和已死的昨晨(Unborn To-morrow, and dead Yesterday.)

根據這個中譯，我們就可以講故事了。

●詩人科學家

《魯拜集》的作者開儼(Omar Khayyam, 1048-1131)是波斯籍學者，生於伊朗東北部的大城內沙布爾──在他那個時代，那裡屬於新興的「塞爾柱帝國」勢力範圍。當時在文化上仍是伊斯蘭世界的黃金時代，但在政治上早已不是阿拉伯帝國的天下。塞爾柱帝國成了新興強權，阿拉伯帝國的「哈里發」淪為類似周天子的角色。

因此對於開儼而言，塞爾柱帝國的「蘇丹」就是他的國君。可想而知，當蘇丹邀請他參加曆法修訂計畫，開儼自然唯命是從，而且很可能覺得十分光榮。時間是公元1073年，開儼當時二十五歲。

修訂曆法是茲事體大的科學計畫，絕對不會邀請詩人來湊熱鬧。這就充分說明一件事：開儼在很年輕的時候已經是知名的科學家。事實上，早在1070年，年方二十二歲的他就寫了一本數學書《代數問題演示》。

這本書的主題之一是一元三次方程式的解法。如果你還記得古希臘的梅氏如何解決「加倍立方體體積」這個難題(等同於解x³=2)，就很容易瞭解開儼使用的方法。因為梅氏是用兩個拋物線的交點得出欲求的解，開儼則是將其中一個拋物線改成正圓。(如果需要複習梅氏的方法，請參考〈無用之用〉這篇文章。)

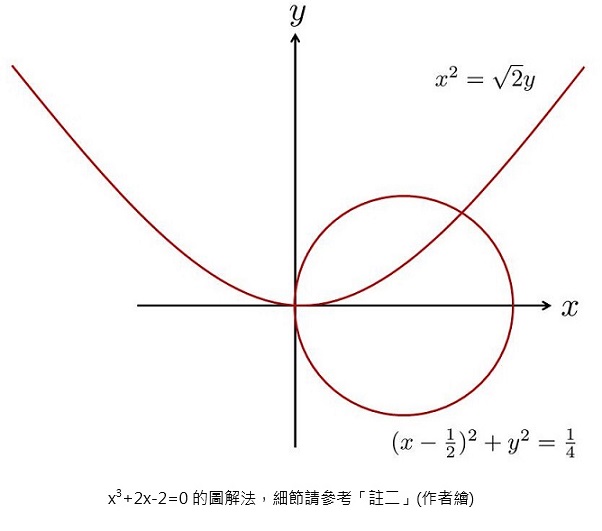
換言之，開儼同樣是使用作圖法，求得一元三次方程式的(其中一個)解。這個方法有兩個缺點，一是無法推廣到複數解，二是無法寫出精確的公式，兩者原因都很明顯。至於真正完美的解法，則要一直等到十六世紀才出現於義大利半島。

無獨有偶，非歐幾何也可算是開儼的另一個未竟之志。1077年，他又寫了一本書《論歐幾里得公理的困境》，試圖用另一組公理取代歐氏(前五個)公理，並仔細探討了三種可能的結果──用現代語言來說，就是歐氏幾何以及兩種非歐幾何──可惜他採取的策略是「證明」只有歐氏幾何正確。

●精確的曆法

開儼在曆法修訂上投入了六年的時間，公元1079年，他們的團隊終於完成了所謂的哲拉里曆(Jalali calendar, 因為當時的蘇丹名叫Jalal.........)。

如果你上網查查，很容易發現如下的論述：哲拉里曆非常精確，甚至超越了幾百年後才出現於西方世界(而且目前仍通用)的格里曆。這到底是不是真的？讓我們抽絲剝繭一番吧。

格里曆(新曆)出現於十六世紀的歐洲，用以取代不太準確的儒略曆(舊曆)，但是過渡期相當長，有將近兩百年的時間，導致十六至十八世紀的歐洲歷史令人相當頭痛。例如牛頓到底生於哪一年，又是卒於哪一年，儒略曆和格里曆都會給你不同的答案(儒略曆1642-1726；格里曆1643-1727)。

大家應該都學過格里曆的規則，簡單地說就是：四年一閏，逢百例外，逢四百又例外。例如公元2000年是例外的平方，所以是閏年而非平年。而根據這個規則，我們就能計算格里曆的一年平均有多少天。

365+1/4-1/100+1/400=365+97/400=365.24250000...日

(過度簡化的儒略曆則是365+1/4=365.250000...日)

格里曆究竟有多麼精確呢？要回答這個問題，當然需要跟真實世界做個比較。比方說，根據目前最新的天文觀測數據，公元2000年共有365.242189日(此即所謂的平均太陽年)，它比上述的365.2425日稍微短了一點。

不過請注意，光是根據這個數據，其實不能驟下斷語。因為地球公轉的週期並不固定，而是不斷在減小(這是由於地球和太陽的距離逐年縮短，不過因為很慢，不值得我們擔心)。舉例而言，天文學家曾推算出公元「零年」這一年共有365.242310日(果然稍長於365.242189日)。

有了這兩個一頭一尾的數據，我們才能肯定地說，格里曆的一年(365.2425日)比公元元年至2000年中任何一年的正確數值都稍微長了點。

現在再讓我們看看哲拉里曆，它的規則很簡單，只有「33年8閏」一條而已，因此一年平均有365+8/33=365.242424...日。由此可知，我們的確可以說哲拉里曆比格里曆精確一點點。

然而真正重要的是，哲拉里曆比之前的波斯曆法都精確不少，所以開儼才會洋洋得意地寫詩自誇。不過請注意，後面那兩句純屬文學筆法，大家千萬不能當真。

●詩人的精神面貌

想要一窺開儼的心靈世界，他的豐富詩作當然是最佳管道。所以讓我們再欣賞兩首，由於個人偏好，我引用的都是黃譯(黃老師請見諒，我把您的標點省略了)。

[56]

　　是非原在有無中(For "Is" and "Is-not" though with Rule and Line)

　　竭想窮思總是空(And "Up-and-down" by Logic I define,)

　　借問一心何所好(Of all that one should care to fathom, I)

　　滿盃春酒漾嬌紅(Was never deep in anything but--Wine.)

[66]

　　欲尋身後路茫茫(I sent my Soul through the Invisible,)

　　自遣離魂到大荒(Some letter of that After-life to spell:)

　　魂魄歸來唯一語(And by and by my Soul return'd to me,)

　　我兼地獄與天堂(And answer'd "I Myself am Heav'n and Hell.")

實在很想再抄幾首跟大家分享，但再抄下去恐怕有違「合理引用」的原則，所以就此打住吧。

註一：不知道大家有沒有注意到，開儼剛好生於比魯尼辭世那一年。在數學史上，這可說是個無縫接軌的佳話。更重要的是，兩位大師都是波斯裔，因此當伊朗政府想要宣揚波斯民族在科學發展上的貢獻，他們兩人雙雙入選。

註二：方程式的圖解法並沒有唯一性，例如開儼在研究一元三次方程式的過程中，至少用過兩種圖解法：[I]拋物線和圓的交點(以x³+2x-2=0為例)；[II]雙曲線和圓的交點(以x³+2x²-2=0為例)，它們分別能轉換成如下的二元二次聯立方程式：

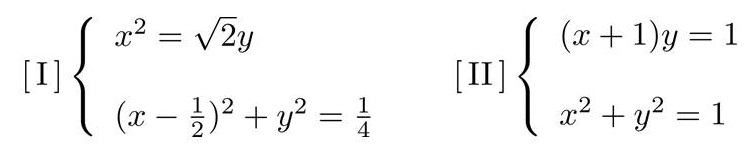
(其中[II]的幾何意義為：一個直角三角形，其斜邊長度等於斜邊高加上直角邊之一，求解這個三角形的邊長比。)

如果你試著消去y, 第一組聯立方程式會轉換成x(x³+2x-2)=0, 第二組則會變成x(x³+2x²-2)=0, 因此兩者的圖解各有兩個交點。扣除x=0這個「人工解」之後，另一個交點的x座標就是答案。

在這兩個例子中，另外兩個解都是共軛複數，當然無法以交點的形式呈現在平面座標上。

註三：如今網路文獻中充斥著哲拉里曆是「2820年683閏」這個說法，其實這是二十世紀中葉才出現的推論，並沒有扎實的證據，絕對不能視為正統史料。

偏偏這個有如沙上城堡的「2820年週期」不脛而走，導致一則以訛傳訛的迷思，認為開儼是先用「精密儀器」測出一年的日數是365.24219858156日，然後再根據這個結果，訂出「2820年683閏」的規則。這是標準的倒因為果，大家不妨算算683/2820等於多少。

再強調一次，在開儼那個年代，除非有外星人協助，人類絕對不可能把「平均太陽年」測到小數點後十一位數(事實上，目前仍舊如此)。