電導率、弱局域化、與量子混沌(上)
■儘管古典的圖像提供了學者們最初階的電導計算能力,但量子效應中不同物質波的建設性干涉仍提供了不容忽視的修正。
撰文|蕭維翰
理論物理學的目的是為物理現象提供一些定量的描述。也因此一個完整的物理理論,應該能計算一些可觀測的物理量。基於人類對電磁現象的掌握,在可測量的一系列物理量中,電阻率(resistivity),或者是它的倒數,電導率(conductivity),大概是最直接的對象了,也因此,本文想趁機談談在一些問題中,物理學家如何從理論模型中得到電導率,而又有哪些因素會影響電導率。
電導率或者電導之所以直覺,是因為他的定義單純:只消在實驗室中打開一個電場(或電位差),然後量測電流的響應[1],電導率即是電流與電場間[2]的比例常數。
電流可以想成是微觀帶電粒子流動造成的現象。如果系統內的帶電粒子在外加電場中,長時間尺度下擁有一個平均的漂移速度(drift velocity)巨觀而言我們會看到帶電的粒子流往某個方向走,就是電流。要研究電流,核心的問題就是粒子在施加電場後有多會跑。
在剩下的篇幅我們嘗試談論這個問題跟一些特徵的時間尺度。
從最古典的圖像出發,一個帶電粒子在電場下感受到電磁力,依循牛頓定律 F = ma 進行加速度運動。如果沒有東西去攔著它,它就會越跑越快,如此一來,長時間下測量到的電導率會是無限大。然而,在一個系統中,還有許多許多的帶電粒子跟其他原子等等結構,上述的粒子沒有辦法暢快地加速,反之,它會步履蹣跚地一路碰撞。簡約地描述這些碰撞效果的參數是「弛豫時間」(relaxation time),它代表平均而言,這個粒子多久會遭遇一次碰撞,這個效果等同一個阻力,長時間下來會形成「力平衡」[3],而粒子們終將達到飄移速率,反映成有限的直流電導率。[4]
接著來想量子效應帶來什麼效果[5]。
在量子力學的框架下,粒子具有波動性,談論一個粒子的絕對位置已經不合適(因為我們還要談論它的動量、能量)根據不確定性原理(uncertainty principle),粒子位置的精確度只能[6]到達它的德布羅伊波長(de Broglie wavelength),這個波長定義了一個長度的尺度,如果這個波長跟「平均自由徑」[7]相比很小,使得這個波包看起來還是像個粒子,我們便稱這個問題是準古典(semi-classical)的。
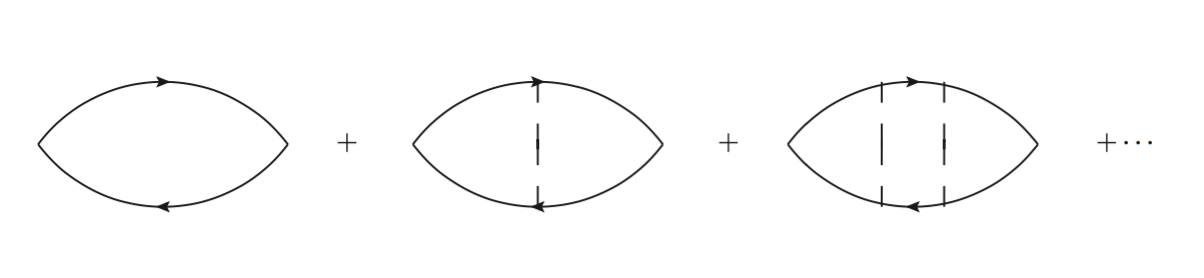
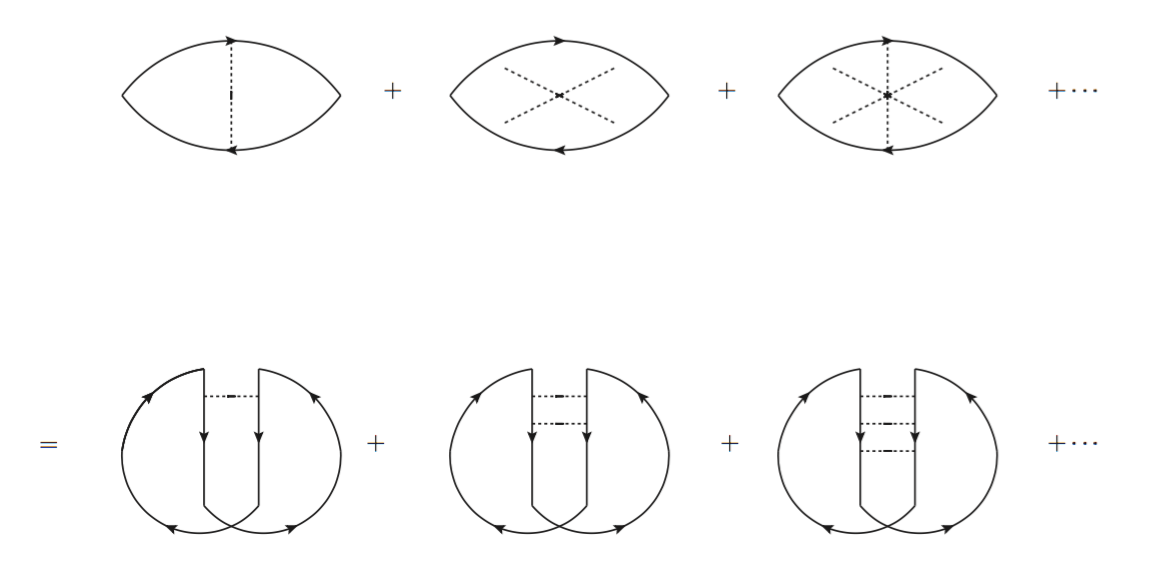
根據費曼,一個粒子從一個點 A 到另一個點 B,它會考慮所有可能的路徑,每一條路徑都貢獻一個機率振幅,將所有的機率振幅加總取絕對值平方後,就是粒子從點 A 到點 B 的機率。在準古典的極限,因為不同路徑間的波包的破壞性干涉,貢獻最大的的確是個別路徑的機率和。
若今天 A 跟 B 是同一個點 O,意即考慮一個粒子從某點出發後,又回到原來那一點的機率,上面這個論述依舊成立,但值得注意的是有些路徑間兩個波可以有「建設性干涉」(見圖三),簡單的估計可以發現,考慮這些量子的建設性干涉,粒子回到原點的機率是古典的 2 倍!
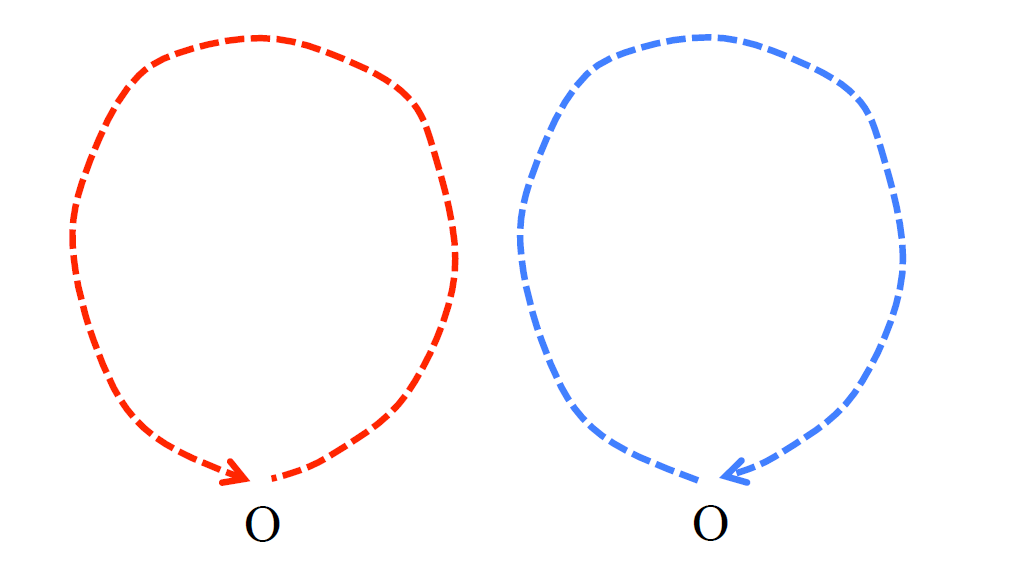
當粒子比較容易回到原點,就表示它比較不容易流走,也從而提升了電阻、減弱了電導。此現象的基礎是物質波之間的干涉,但波與波之間的相干性(coherence)很可能在與雜質散射的過程中減弱,這個效果在現象學上由另外一個時間尺度「相干時間」(coherence time)描述,代表平均經歷多長的時間,波包間會喪失相干性。在低溫,這個與雜質和交互作用強度無關,而跟空間維度有關的現象稱為弱局域化(weak localization)。在2維系統局域化的強度正比於相干時間與弛豫時間的比值的對數。
至於混沌現象如何切入來影響弱局域化的結論,就讓我們在下文討論。
註解:
[1] 當然實際上的操作沒這麼單純,但大概念上是如此。
[2] 更精確地講是電流密度與電場間。
[3] 瞬時來看當然沒有平衡,這是一個長時間後的淨效果。
[4]這個看法在量子力學出現以前已經存在,教科書中稱之為 Drude model,令人驚訝的是,即便考慮第一階的量子力學修正,整個解的形式並沒有改變,僅僅修正弛豫時間的強度。
[5] 讀者們可以去複習某一期探索,這邊講述的術語應該在那裡都找得到。
[6] 我並不是在說量測,而是即便在理論上「談論」,我都不應該超過這個精確度。
[7]約略而言是弛豫時間乘上費米速度,也就是一個粒子平均走多遠會碰撞一次。原則上是要考慮經過量子修正的,因為不是所有的碰撞都會影響電導的效能。
參考資料:L. Altshuler, A. G. Aronov, A. I. Larkin, D. Khmel’nitskii, Anomalous Magnetoresistance in Seminconductors, J. Exp. Theor. Phys. 54, 411 (1981).
--
作者:蕭維翰,臺大物理系畢業後逃到芝加哥,吹風吹雪之餘,做研究讀博士班。可惜離開臺灣後無海可看,只能在密西根湖旁揀一方堤岸,偽裝成看海的人。科教中心特約寫手,從事科普文章寫作。
