【大宇宙小故事】16 阿基米德與漢尼拔
撰文|葉李華
這兩個人在歷史上赫赫有名,一位是大科學家,一位是震古鑠今的猛將,想必你或多或少都有印象,例如阿基米德擁有許多偉大的發明與發現,而漢尼拔曾經率領大軍翻越阿爾卑斯山,橫掃義大利半島,把羅馬打得潰不成軍。但是,你可知道他們兩人有什麼交集嗎?

●阿基米德不是希臘人?
阿基米德通常被視為古希臘的科學家,但無論就歷史或地理而言,「古希臘」都是相當攏統的名詞。以阿基米德為例,他是公元前三世紀的人,那時古典希臘時期已經結束,進入了所謂的希臘化時代。而且嚴格說來,阿基米德也不是希臘人,而是「敘拉古」這個城邦王國的公民。
敘拉古(Syracuse)在哪裡?這個古城位於西西里島的東岸,而西西里島則在義大利半島的南端(有人將它比喻為靴尖上的足球,夠傳神吧)。因此,就當時的政治勢力而言,敘拉古在羅馬共和國的腳底下。即便如此,它仍然是個獨立的政體,這點相當不容易。
不過一旦遇到戰亂,這樣的小國家很難保持中立,通常都不得不選邊站。而在阿基米德有生之年,如此的戰禍出現過兩次,史稱第一次與第二次布匿戰爭──其實還有第三次,但阿基米德看不到了。
三次布匿戰爭,交戰雙方都是羅馬和迦太基這兩個地中海強權,而且最後都是羅馬獲勝。之所以稱為「布匿戰爭」,是因為迦太基人乃是腓尼基人的後裔,而「布匿」正是「腓尼」的轉音。由此可知,迦太基不會採用這個名稱,但在第三次布匿戰爭後,迦太基慘遭亡國滅種的命運,因此這些戰爭並沒有「迦太基史觀」的文獻流傳下來。
第一次布匿戰爭,敘拉古選擇加入羅馬共和國的陣營,因此戰後得以在西西里島保持一枝獨秀的獨立地位。
然而,第二次布匿戰爭期間,在迦太基主將漢尼拔的策動下,敘拉古選擇了倒戈。
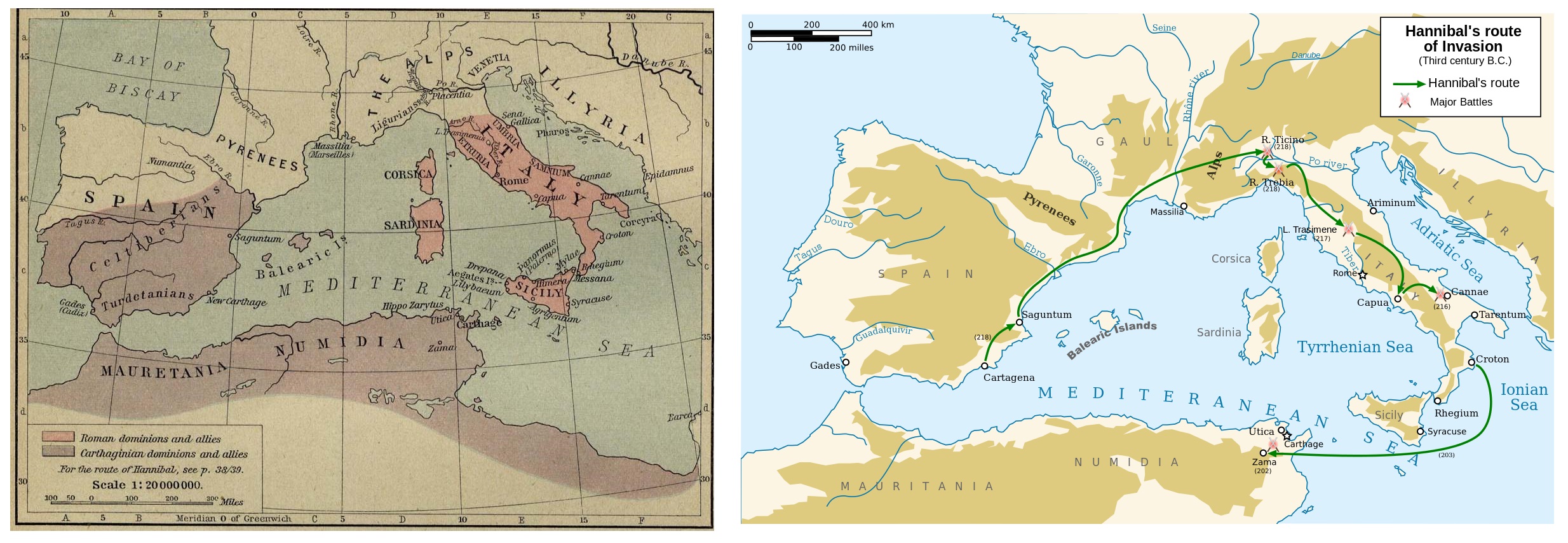
看到這裡,你應該能回答開頭那個問答題了。
不過,既然是問答題,當然沒有標準答案。比方說,你可以簡單回答:他們兩位是同一個時代的人(因為阿基米德經歷了第二次布匿戰爭,而漢尼拔是這場戰爭的主角)。但只要你稍微動動腦,就能想出一個比較深刻的答案:阿基米德與漢尼拔曾經是盟友(因為在第二次布匿戰爭中,敘拉古曾與迦太基結盟)。
可是,還有沒有更深刻的答案呢?有的,那就是漢尼拔這個盟友太差勁,所以我們要把阿基米德的死記在他頭上!
原因很簡單,敘拉古與迦太基結盟之後,很快便受到羅馬軍團來自海陸兩方的圍攻,前後長達兩年之久。漢尼拔雖然伸出援手,可惜以失敗告終。不久之後,敘拉古便城破國亡,而阿基米德也慘遭殺害。這筆帳,請問該不該算在漢尼拔頭上?
●科學家兼發明家之死
既然漢尼拔的馳援並不成功,小小的敘拉古怎麼撐得了兩年?答案近在眼前──當然是阿基米德的功勞。
在敘拉古被圍期間,阿基米德發揮書生報國的精神,為敘拉古發明了許多精銳的武器。在這些武器中,最神奇的應屬下面這兩樣:
一、能擒拿敵艦的鐵爪:有八成真實性。雖然由於時日久遠,具體結構眾說紛紜,但一定是利用槓桿原理。
二、能燒毀敵艦的死光:純屬傳說。即使真有這樣的反光鏡,殺傷力也僅限於心理層面──哎呀,敵人請到太陽神助陣啦!
看到這裡,或許有人覺得恍然大悟:阿基米德發明了那麼多兇猛的武器,羅馬軍團自然恨他入骨,因此城破之後,他當然難逃一劫。抱歉,並不是那麼回事。
根據可靠的史料,攻城的羅馬將領深知阿基米德是偉大的學者,下令不得動他一根汗毛。然而,不知是命令未及傳達,還是有人故意抗命,總之不久之後,阿基米德便死於羅馬士兵之手。時間是公元前212年,阿基米德大約七十五歲。
傳說中,城破之際,阿基米德仍在專心研究幾何問題(並非埋首書案,而是埋首沙堆)。當羅馬士兵來到他面前,阿基米德義正辭嚴地說:「別踩壞我(畫)的圓!」不料,這句話竟成了他的遺言。
但根據歷史學家的考據,這句「遺言」應該是後人偽造的。話又說回來,就算只是小說家言,也充分反映了阿基米德在數學史上的地位。
至於在這項傳說中,阿基米德為何要說「別踩壞我的圓」,而不是「別踩壞我的拋物線(或螺線)」,想必是因為在他的眾多數學成就中,「圓周率」是最耀眼的一項。
如今,小學生也知道圓周率大約等於3.14,但很少有人知道這兩位小數來之不易,而第一個算出3.14的人正是阿基米德。在他之前,四大古國的數學家都沒算得那麼準,例如中國古代通用「徑一周三」這個概念(也就是把圓周率視為3.0),其他古國也頂多精確到3.1而已。
更重要的是,阿基米德計算圓周率的方法不但巧妙,而且極具啟發性。
●圓周率的世界紀錄
根據定義,圓周率是圓周長和直徑長的比值。直徑是一條直線,很容易量出它的長度;但圓周有弧度,當然無法用直尺測量,因此要計算圓周率,就得先想出測量圓周長度的(間接)方法。
阿基米德發明的方法如下:先畫一個圓,然後在內外各畫一個緊貼著它的正六邊形(數學術語是「內接六邊形」與「外切六邊形」)。這麼一來,圓周就被夾在這兩個六邊形之間,所以外面那個六邊形的邊長一定大於圓周的長度,而裡面的六邊形邊長則比圓周小。換言之,這兩個六邊形的邊長構成了圓周長度的上下限。我們可以直接測量這兩個邊長,但難免有誤差;如果用幾何公式來計算,則能得到絕對精準的數值。
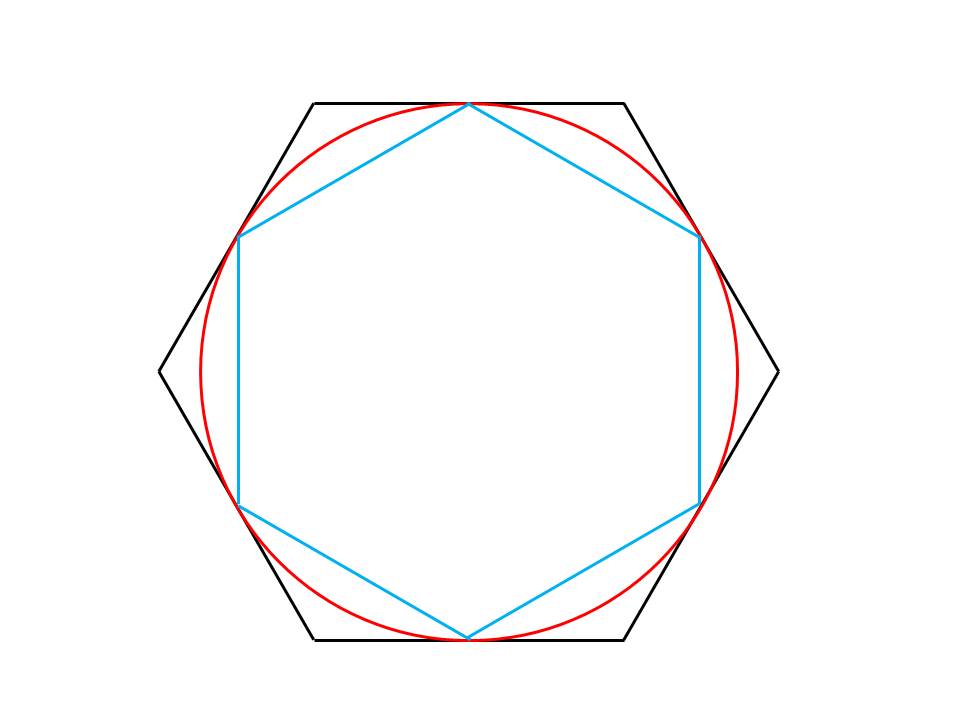
然而,兩個六邊形所提供的上下限範圍太大,無法產生比3.0更精確的圓周率,因此阿基米德繼續努力,改用兩個正12邊形來夾擊圓周的長度,可惜結果仍舊不理想(除以直徑後,下限是3.10..., 上限是3.21...)。阿基米德並不氣餒,又陸續改用正24邊形、正48邊形、正96邊形──最後這一組,終於夾擊出相當精確的圓周率近似值(下限是3.1410..., 上限是3.1427..., 由此可知前兩位小數一定正確)。
在世界數學史上,這個紀錄保持了近五百年,才被公元三世紀的中國數學家劉徽所超越。至於名氣更大的祖沖之,則是站在劉徽的肩頭更上一層樓。
●不以成敗論英雄
既然被譽為古代世界最偉大的數學家,阿基米德在數學上的成就當然不只圓周率而已。比方說,有些數學史研究者甚至認為阿基米德差一點發明了微積分。這雖然是比較誇張的說法,但或多或少仍有所本,例如我們知道阿基米德已充分掌握無窮級數的訣竅,而無窮級數與積分可說僅有一線之隔。
總而言之,請千萬別懷疑阿基米德在數學史上的頂尖地位──不但是古代最偉大的數學家,還是古往今來三大數學家之一。巧合的是,在世界軍事史上,本文的另一位主角也享有類似的地位,可見史家並不以成敗論英雄。不過,倘若漢尼拔拚了老命解救阿基米德,讓老科學家能繼續發揮餘熱,想必後人會更加敬佩他。
