【物理世界】左與右，固態系統中的ABJ異常
撰文｜蕭維翰
若宇宙中只有一隻手，我們是否能區分他是左手還是右手呢？哲學家康德討論過類似的「不一致的對等物間的關係」，亦即左右手的差異是內在性的，還是由他們與外界的關係決定的。[1]暫且擱置哲學方面的思考，日常生活中，左手與右手的差異還是滿明顯的（比如說買手套時，左手戴不進右手的模板），他們的關聯必須透過鏡像來建立：在鏡子中，左手變成了右手，反之亦然。
在化學中也有一些化合物互為對方的鏡像，這類的分子我們稱為鏡像異構物，如葡萄糖就可以分為左旋糖和右旋糖，人類體內的酵素，基本上只代謝右旋糖。實驗上我們要如何區分這些異構物呢？總算輪到物理學家出場，我們可以透過光學方法：用光去照分子後，右旋分子只會放出右旋光，左旋分子則只允許左旋光被散射。[2]也就是說，光子也具有這種類似左手和右手的差別。
其他基本粒子也能以這種性質區分嗎？
之前探討 Majorana 粒子時，我們提及它是 Dirac 粒子這個家族中的一個成員。這個譜系其實還有其他分法，比如一個 Dirac 粒子可以分為左手性的跟右手性的粒子，只是對於像電子這種有質量的粒子，這樣區分意義不大，因為在有質量的情況下，左手性的粒子可以轉為右手性的粒子，右手性也可以轉為左手性。另一方面，在不考慮量子效應的時候，用手性來區分無質量的 Dirac 粒子就比較有意義，我們可以將一堆電流分類，說這一部分的電流是左手性的電流，另一堆是右手性的電流。因為沒有質量可以把粒子的手性改變，左右手性的粒子數在古典情境下各自守恆，也因此加起來總電荷也是守恆。更精確一點說，我們可以計算在經過交互作用後，右手性粒子數的變化量 
與左手性粒子數變化量 
的差 
，以及他們的和 
這兩個數值，古典上 、 都是 0 ，因而 
。
考慮量子效應（也就是計算比較複雜的費曼圖），高能物理學家在計算中了解到他們沒辦法自洽地讓上一段所提及的差與和同時是 0，至少得放棄其中一個關係 [參1,2]。因為兩者的和代表電荷守恆，對於科學界來說這個關係是比較重要的（在日常生活中，電荷在實驗的精確度下幾乎完全守恆），暗示我們必須放棄 
。這件事情被稱為Adler-Bell-Jackiw手徵異常（ABJ Chiral anomaly）[3]。很快地物理學家理解到若想要合理解釋一些衰變過程，例如一個介子 
衰變成兩個光子，手徵異常必須是「正常」[參2]。
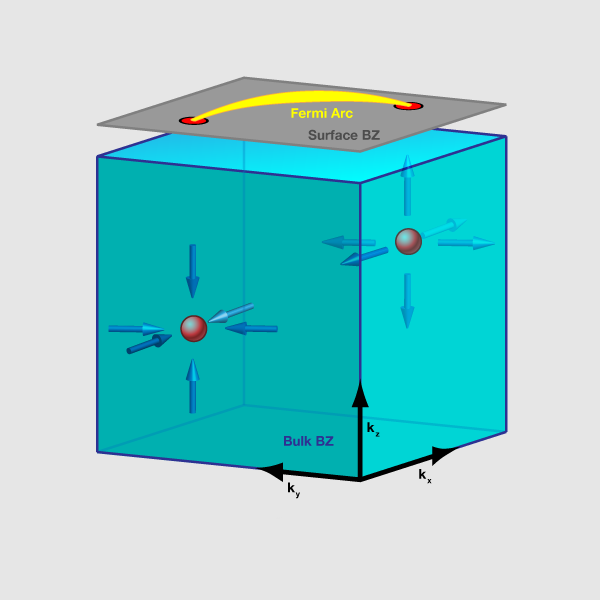
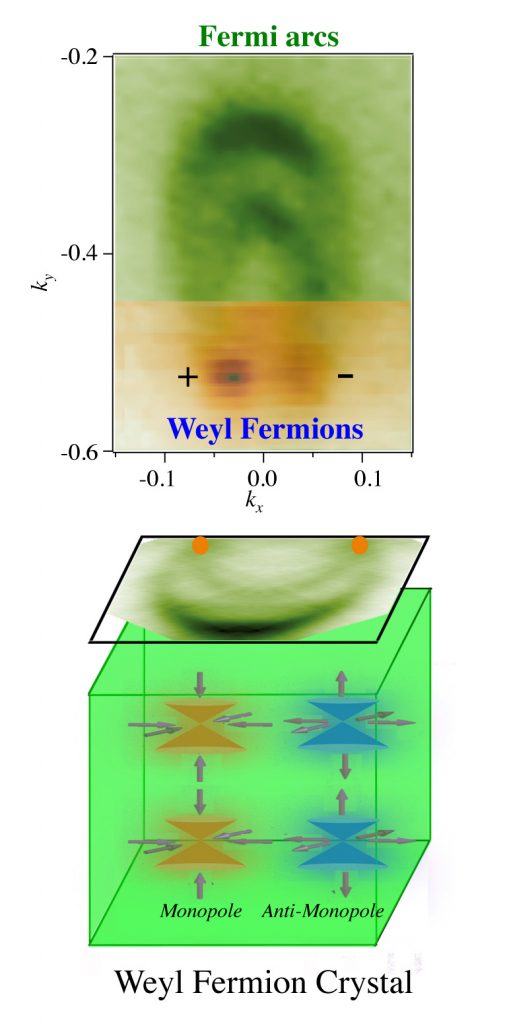
如在 Majorana 粒子文中所言，固態物理中雖然沒有像高能物理那樣的粒子圖像，但也因此成為實現許多想法的場所。近幾年來固態物理界有一個新興的領域叫做 Weyl 半金屬 （Weyl Semimetal），這種材料的光譜中會成對出現一些 Weyl 點，意指系統在這些點附近看起來像 Weyl 粒子，這種粒子也是 Dirac 粒子家族中的成員，但帶有明確的手性[4]，這提供了我們在小實驗室中研究手徵異常一個很好的平臺 [參3]。2016 年 4 月由 Princeton 大學 Hasan 研究組與北京大學 Jia 研究組為首的跨國團隊在 Nature Communication 發表砷化鉭 （TaAs） 材料中觀察到的ABJ 手徵異常跡象 [參4]：該文中指出，透過測量材料在施加平行的電磁場下的磁阻，並分析所有的因素，他們得到由手徵異常所導致的負磁阻現象。
在理論學家這端，固態與高能領域的界限早已愈來愈模糊，在實驗端，ABJ 手徵異常在固態系統中的發現，也算是進一步肯定以固態物理研究所謂「基本物理定律」的可能性。
參考文獻：
- Adler, Axial-Vector Vertex in Spinor Electrodynamics, Phys. Rev. 177, 2426 (1969).
- J. Bell and R. Jackiw, Nuovo. Cimento. A 60, 47 (1969).
- -Y. Xu et al, Discovery of a Weyl Fermion Semimetal and Topological Fermi Arcs, Science 349, 6248, 613 (2015).
- -L. Zhang et al, Signatures of the Adler-Bell-Jackiw Chiral Anomaly in a Weyl Fermion Semimetal, Nat. Commun 7:10735 (2016).
註解：
[1] 關於左右的探討，可以參考高涌泉教授在科學人的文章〈左與右〉或者在 Youtube 上的影片： Symmetry and symmetry breaking in Physics I 。
[2] 左手與右手的分辨，是一種叫做手性（chirality）的性質，但旋光性看的其實是 helicity ，數學上這兩者並不完全一樣，只是在我們接下來要討論的問題裡（無質量粒子）兩者的關係十分親密，即便在專業書刊、文章也時常混用。
[3] 這名字其實很妙，因為有考慮量子效應的結果是比較精確（或正確）的，但因為跟人類原先的經驗不一樣，所以我們還是稱它為異常。
[4] Weyl 點基本上都是成對出現的，大家可以想像他是一個 Dirac 點退化成兩個點，就像一個無質量的Dirac 粒子可以區分為兩個 Weyl粒子。
--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。
