【探索15-5】螢火蟲的數學習題：同步現象的過去、現在、未來
講師｜交通大學應用數學系 莊重教授
撰文｜沈君宜
●「同步現象」有多熱門？無所不在的同步現象
在Google Search上，最常見的英文字 “the” 可以見到 
數量級個條目；synchronization （同步）這個字，竟然也有 
條，和 quantum mechanics（量子力學）及知名球星Stephen Curry 位列同等級；甚至 general relativity（廣義相對論）和 Jeremy Lin（林書豪）都得甘拜下風。同步現象之所以如此眾所矚目，不難想像它是跨領域、跨尺度的。舉凡數學、物理、化學、生物、天文等自然科學領域，乃至工程、經濟、社會學，都少不了它參一腳；尺度更是橫跨奈米到天體，大小通吃。 “Pervasive, ubiquitous, and omnipresent.” 恰可為同步現象下註腳。
歷史上，同步現象寫下的故事自也佔有一席之地。2000年完工開放的倫敦千禧橋（Millenium Bridge），慕名而來的人潮眾多；其水平頻率與參觀人潮行走頻率相互影響、加成，所導致劇烈搖晃使它被迫關閉。大尺度的同步現象——比如太陽系中小行星帶的重力同步——對一般人而言似乎遙不可及，但中尺度的例子想必耳熟能詳：螢火蟲、鐘擺、鳥、蟋蟀、電力系統，甚至女生室友經期的同步。其他像是心肌節律細胞（pacemaker cells, p-cells）、腦神經元、生理節律細胞（circadian cells）、電子，又把同步現象擴展到了細微處。腦部疾病、認知記憶，與同步現象都脫不了干係：研究顯示，記憶新事物時，特定腦區會成同步狀態；若是自覺健忘，大概也可以怪罪同步現象的失調吧！
大千世界由各種生物和無生物所組成，同步現象兩系統中均未缺席。同步的基本概念認為，自然界存在各種「振盪器（oscillators）」，舉凡一隻蝴蝶、一個節律細胞，都可以稱作一「振盪器」。看似彼此為獨立個體，但自然界存在各式各樣的管道，讓它們得以相互交談。交流的目的，便是達到和諧、同心、一致了。這樣的規律，早在兩千年前（400 B.C.）就有跟隨亞歷山大大帝南征北討的部屬 Adrosthenes 記載。然而，科學史上正式的紀錄，則要追溯到西元1665年的惠更斯。當時的計時工具，每天可以慢上15分鐘，但他做的擺鐘，提高了幾百倍的計時精準度。時值航海時代之始，本來人們期待以準確的計時器協助經度劃分，可惜最後在風浪顛簸中，擺鐘未能完成任務。但有一天，惠更斯休息時看見掛在牆上的兩擺鐘，似乎出現了相位相差180度（方向相反、速度相同）的同步擺動的現象。不論惠更斯如何實驗、撥亂擺鐘、改變它們之間的距離，只要掛在同一面牆上，最終都能回到同步。他將此事於書信中與父親交流，「同步現象」也因而在科學史上留名。
●螢火蟲的啟示
生物界的同步現象中，當屬螢火蟲成名最早。1915~1935年間，「科學（Science）」期刊中，共有21篇論文以此為主題。究竟是巧合、是環境因素，或是蟲群中有一「領導者」，眾「蟲」唯牠是從？直到1960年代，有系統的說法漸趨成熟：每一螢火蟲都有自己內在的頻率、自己的週期與循環；同時，每一隻螢火蟲也都會根據夥伴的頻率做調整。但對於雄蟲同步發光的意義，求偶、競爭、合作等可能性，眾說紛紜。這個話題紅極一時，甚至曾遭到美國眾議院議員批評：「花納稅人的錢研究螢火蟲發光，簡直浪費公帑！」誰知，後來這看似無用的研究卻神奇地有了應用之處——路由器（routers）的同步，使資訊傳播遇到了阻礙；由螢火蟲身上習得的知識，恰恰可提供啟示。科學、數學上，「無用之用」往往毫不留情的「打臉」短視近利的人們。
生物學範疇中，心臟的節律細胞（pacemaker cells, p-cells）同樣引領好一陣子的風騷。擁有數學及生理醫學雙學位的美國國家科學院士 Charles Peskin，以方程式敘述p-cells 本身的內在時鐘及與周遭的互動機制：第一個方程式，描述每一個細胞有自己的電壓及能量，直至跨越閾值，旋即瞬間釋放能量後歸零。而它們的互動方式是「各玩各的，只有瞬間互動」——唯有某些細胞達到門檻放電時，彼此之間才產生交流。式子中的Ti 表示跨越門檻的時間，wij 則是影響到其他細胞、為其他細胞增加的能量。
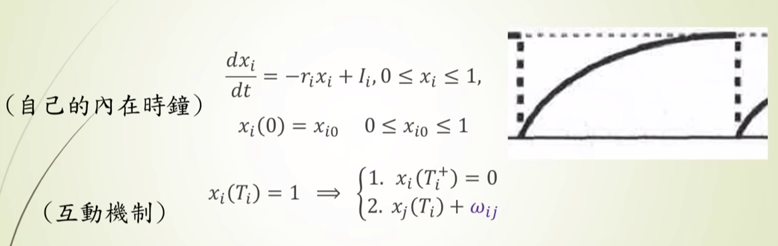
看似十分合理的數學模型，卻因為函數不連續而處理不易。於是Peskin 猜測：一可能是所有的p-cells 都是相同的（identical oscillators），二是彼此有微小的差異（non-identical oscillators）。不論哪一種，皆可以達到最終的同步；也分別在1990年由 Mirollo & Strogatz 、2008年由莊重教授及其學生，成功解題。同樣的概念更可以用在地震的模擬，將板塊等同 p-cells、壓力類比電壓；超過能量閾值後，一板塊的運動會引發另一板塊的響應，是以大地震後的餘震不斷。
提到同步，不能漏談勤奮數學家 Norbert Wiener 的小故事。一日，他準備搬家，妻子深諳他的性子，因而將新家的地址寫在紙上備忘。然而到了下班時間，那張字條早就成了 Wiener 的計算紙。他到了舊家才猛然想起這事，急忙抓了路邊的小女孩，問：「你知道 Wiener 先生一家的新地址嗎？」不想小女孩答道：「我知道啊，爸爸。」如此一位廢寢忘食的數學家，對同步現象有觀念上的貢獻；他是第一個處理巨量的個體、指出同步現象無所不在的人，也以α波的研究留名。他並提出在一性質的分佈上，「中間」的力量是最為強大的，也將逐步累積而增加。時值學生Art Winfree 初入大學，他將Wiener 此一想法化為模型。這是一個與位置相關的「叫與聽」的函數；第一項大於第二項時，會「叫」第二項增加速度，反之則「叫」它減速。此模型因為過於複雜且非線性，只能仰賴電腦幫忙運算了。Winfree 並在思考實驗中，提出同步狀態的達成，與群體的「均勻度」相關。
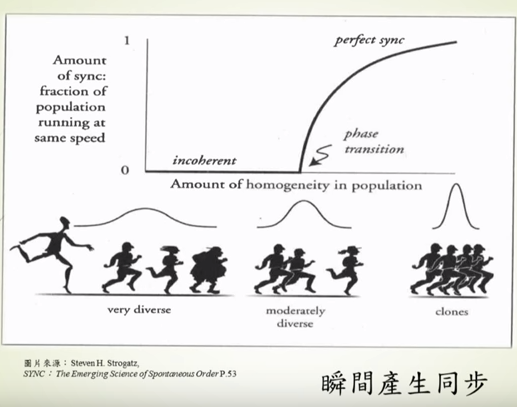
Winfree 固然天才無比，其模型仍嫌繁複；Yokishi Kuramoto 則矯正了此一缺點。他將 Winfree 的叫聽函數改成「看」的函數，改為與位置無關，並增加對稱性。所謂的「看」，指單一的振盪器計算與他人的相對位置，加以平均後作為矯正之標準。這樣的矯正隨時進行著，系統中的每一振盪器也都參與其中。經過這個巧妙轉換，理論分析的可行性大幅提升，Wiener 與Winfree 亟欲觀察的現象也得以展現。接下來，1973年的諾貝爾得主Brian Josephson 觀察「量子同步」的現象：將上兆個同步的庫柏偶（Cooper pair）電子通過絕緣連接板而產生超導。雖然尺度相差甚大，但與鐘擺的同步，卻可以用相同的簡單微分方程式描述。數學在同步現象上的貢獻，至此已無庸置疑。
●革命尚未成功，同步仍需努力
至於當紅話題「混沌」是否也可同步？物理學家Pecora 以此為壯志，最後「以混沌制混沌」的方法終於成功。Satake 與 Iwasa 「森林與開花的樹」更談到自然界中的混沌與同步——每一棵樹具有一個生理時鐘，本身即可能有一週期、亦有可能為混沌。有趣的是，它是一個離散型的函數，每年當作一不連續的單一時間點；彼此之間的互動則屬於不平滑的互動方式。
科學與數學上的難題，經常被普羅大眾詬病脫離生活。但同步現象近年已然超脫單純的數學之美、研究樂趣，在諸多領域皆有佳績——常見的GPS、雷射、醫療上令人頭疼的癲癇，甚至機翼的裂縫與地底的石油。交通大學的實驗室也推出可加密通訊訊號的函數，製造出好用的混沌，並通過美國國家安全局的亂數檢驗。
眾多科學家的齊心協力下，同步現象的了解與模擬堪稱大有進展。大業完成了嗎？當然不。許多數學上可證明的現象尚未經過實際的實驗觀察，是一大根本問題。至於同步現象可否跳脫自然領域，走入社會？考量人類世界的錯綜，或許又是漫漫長路了。
--
本文整理自：105/5/14 由莊重教授在臺大思亮館國際會議廳所主講之「同步現象的歷史、數學和應用」演講內容。
