【探索15-4】花豹的斑紋與數學不得不說的故事

講師|中興物理系 廖思善教授
撰文|陳文翊
●花豹斑紋跟碎形
花豹的斑紋是怎麼形成的?仔細看花豹的斑紋發現它似乎像是之前介紹過的碎形。在問花豹的斑紋是不是碎形前,需要先了解碎形是甚麼?雖然數學上對碎形有更嚴謹的定義,但在這裡我們只討論碎形的一些特性:一個是它在不同比例尺下依舊維持著圖形的結構,並不是毫無規則的出現,這某種程度說明了「有序」的概念;二是圖形有自我相似性。現在回頭來看花豹的斑紋,發現的確呈現有序以及自我相似的特性,因此可以視為一種類似碎形的圖案。
●花豹斑紋跟混沌系統
又問,花豹斑紋跟混沌的關係?混沌最重要的特徵是對初始條件敏感,一開始一個小小的變化,後來造成的影響會越來越大無法預測。混沌系統的背後是一些微分方程式,這些微分方程式會有奇異吸子 (strange attractors),像是 Lorenz attractor,這些吸子會使整個系統出現一幾何圖像。又奇異吸子是怎麼產生的?它可以由簡單的吸子之間的競爭產生,若平面上只有一個吸子的話會把點都吸過去,但如果一個平面上同時存在好幾個吸子,又會發生甚麼事呢?舉個例,像是謝爾賓斯基三角形(Sierpinski triangle),在這個圖形上有三個吸子,所有點有的機會被三個點吸引,出現的點落在後來會形成謝爾賓斯基三角形的位置上,而且不會重複,一開始圖形可能還不明顯,但等到出現的點夠多後,漸漸的有自相似性的三角形們就會出現了,這些點跳動的軌跡無法預測,因此是個混沌的系統。又謝爾賓斯基三角形是一種碎形,跟其他的碎形一樣,可以從奇異吸子中產生。
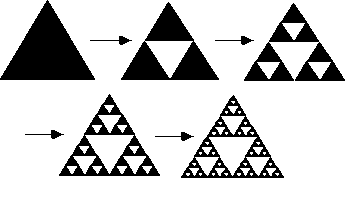
●花豹斑紋形成的原因
現在討論花豹的斑紋是怎麼形成的?有一種觀點是目的論,意思是它的形成是有跡可循的原因,像是螺旋葉序形成的原因,或許是為了讓每個葉片都可以照到充足的陽光。在這裡不得不提一個與之相關有趣的數學關係,先把植物由上往下看,讓它變成一個平面的圖像,如果我們把葉片當作是一個點,每個點跟點之間比較,較相近者相連,並一路連到植物的中心,會發現每一條線都不會重疊。要怎麼擺這些葉片才可以這樣呢?試想如果是每隔60度擺一個,那擺六個葉片就會重複,所以角度不能擺360度的因數,甚至是選無理數當作角度。其他也會呈現螺旋線的,舉例松果,松果可以畫出左旋跟右旋的螺旋線,更巧的是,左右螺旋的數量分別是8跟13條,這令人想起費布那西數列 (Fibonacci number),費布那西數列也有一些有趣的特性,像是如果把相鄰兩數,前者除以後者的結果取極限,會得到一個無理數,換算成角度就會是黃金角,常常兩兩螺旋葉相鄰的角度會接近這個角度。另一種花豹會形成斑紋的觀點是從達爾文出發,抱持的論點是,天擇的基本單位是基因,然後基因是自私的,它們會運用自私與利他的各種策略,使自已成為最具競爭力的複製者。
●斑紋的成長與型態
在這裡不得不提由艾倫·圖靈提出,並由 Hans Meinhardt、Alfred Gierer 等後來的科學家持續修正的數學模型
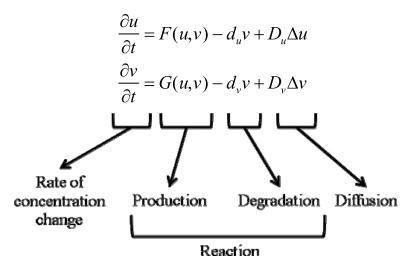
圖靈原本的想法類似這樣:一個原本是圓形的馬胚胎,如果不經過反應跟擴散,是不會形成馬的形狀的。也就是說一個原本可能是均勻、對稱的物體在經過 reaction-diffusion system 後,可以改變物體原本的形狀。在這個模型裡面有兩種不同的分子,稱作 morphogens,它會透過 reaction-diffusion system 建立起不同的化學梯度(gradients)。為了要得到最後可以穩定一段時間的圖形,必須要對這個系統作假設,假設 morphogen A 可以自我催化,所以A產生的速率會正比於A現在的數量,又A它也會促進另一個 morphogen B 的形成,B的功能是抑制A的形成,因此這個系統是在A的自我催化跟B的抑制中競爭,如果要形成一個穩定的圖形,則B的擴散速度要比A還要快,這意味著A的自我催化會讓A在某些位置數量是佔有優勢的,但在遠離這些位置一些距離後會被B給抑制,B有較快的擴散速度確保在小範圍裡不會抑制A的產生,因為B消散的太快了。因此A跟B在整個圖上不同的位置有不同的數量,使整個系統不再像是原先那樣均質。圖靈提出的數學模型提供一個,討論花豹斑紋怎麼形成的方向,廖思善教授利用此方程式,分成兩階段設定參數,模擬出近似花豹斑紋形成的過程。
●結語
但花豹斑紋的形成就是這樣嗎?所有形狀、斑紋不能只是從表面上看到的就去臆測,應該要多去仔細研究背後的原因是甚麼,達爾文的天擇說,形式源自功能上的需求,但天擇並不能回答「如何」的問題,花豹斑紋的形成可能有很多種答案,而跟物種演化有關的基因,並不是生物問題的終結,而只是個開始。最後,有沒有甚麼語言可以描述這些圖形、形狀呢?或許形狀的自然語言是數學,而形狀的形成機制是物理。
參考資料:
1.Nature’s Patterns – A Tapestry in Three Parts, Philip Ball, Oxford (2009)
2.Two-stage Turing model for generating pigment patterns on the leopard and the jaguar, S. S. Liaw et al, Physical Review E 74, 011914 (2006)
3.Nonlinear Dynamics and Chaos, Steven H. Strogatz
4. 生物世界的數學遊戲,Ian Stewart著,蔡信行譯,天下文化 (2000)
--
本文整理自:105/4/30 由廖思善教授在臺大思亮館國際會議廳所主講之「花豹的斑紋與數學不得不說的故事」演講內容。
