【摺紙專欄】淺談摺紙數學與機構

文・圖/ 臺北科技大學機械工程學系副教授 王金樹

摺紙是簡單易學的空間藝術表現形式之一，欣逢國立歷史博物館展覽之「生之世界」摺紙藝術展，邀請多位國際知名藝術家之作品，例如Dr.Bernie Peyton及台大生命科學系于宏燦教授提供多方之協助，相當雅俗共賞，本人有幸欣賞多位作品，發現摺紙到底是「偶然」或「必然」呢？其中「偶然」是指摺紙作者依據自己之藝術抽象而「萃取其形」且意念完成；「必然」是摺紙作者依據物體抽象之「形」，將其「形」靠數學技巧(空間最佳化optimization)，計算出山線(Mountain Line)(M)，谷線(Valley Line)(V)，而完成。且遵守M-V=±2之數學差本文將淺談「必然」之功夫手段，介紹Robert J.lang之Tree maker軟體(可免費下載5.1版)，如何使用與萃取摺紙之三步驟如下：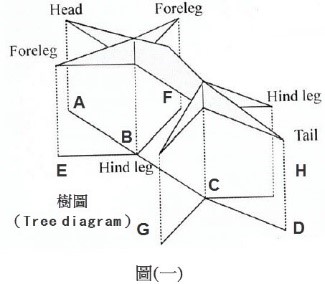

步驟一：如圖(一)，吾人可萃取抽形四肢動物之基本四肢架構且由往下投影至摺紙紙上而得到四肢動物之樹圖(Tree diagram)之骨架圖。

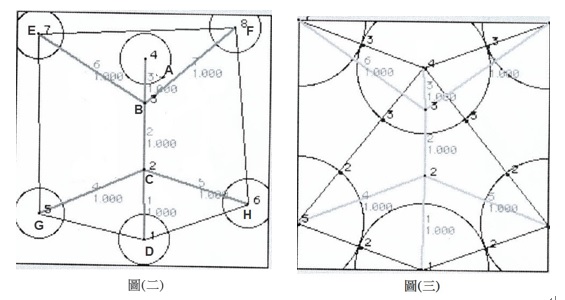
步驟二：如圖(一)其中所有轉折點，區分為端點(Terminal Point)：A、D、E、F、G、H及內部點(Internal Point)：B、C將樹圖之端點畫圓形，如圖二。再利用執行最佳化形成Design View圖(三)，形成相切圓之最佳化圖。

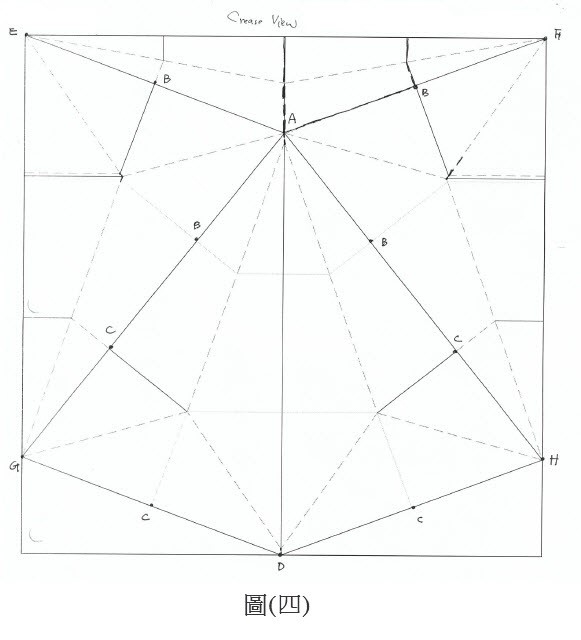
步驟三：選擇Crease View之表現如圖四所示

觀察實線(山線Mountain Line)，內部虛線(虛線Valley Line)稱作用多邊形（Active Polygon)。

其中吾人發現△EAF，△EAG，△FAH為作用之基本三角形，與四邊形AGDH稱為作用四邊形，皆可形成基本摺紙單元。

其中摺紙即由調整A、B、C、D、E、F點之位置往摺紙外緣(最大摺紙利用(Optimization)最佳化計算)

吾人淺談Tree Maker之最佳化步驟而得到摺紙為「必然」，非「偶然」為設計之重點，希望引起大家對「抽形摺紙」的興趣。

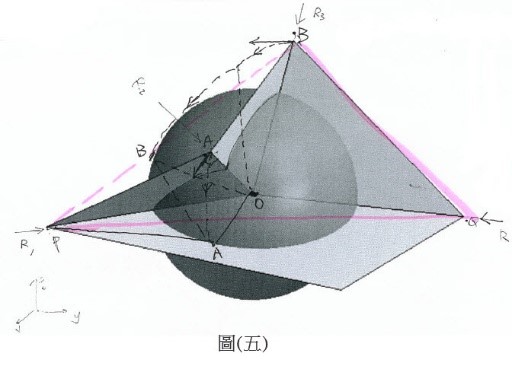
吾人最後要介紹湯瑪斯赫爾(Thomas Hull)，他將摺紙視為摺紙之折點O及運動點A、B之運動，可視為投影至球體的數學模擬圖，如圖五所示。

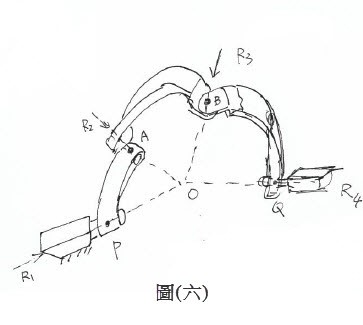吾人發現圖五，因線段PA、線段AB、線段BQ皆為剛體定長且繞其瞬心(O)，如圖(六)在機械上稱為球面4R機構，故摺紙在空間上為R1、R2、R3、R4，四個旋量(Screw)共點，其自由度為三，但當摺紙至平面上時為R1、R2、R3、R4平面上退化為二自由度，故有趣的是，摺紙可當作空間旋量機構之分析。

以上吾人淺談摺紙與數學及機構之有趣相關，拋磚引玉，可望多位有興趣者繼續發展摺紙技術。

※本文刊載於國立歷史博物館歷史文物月刊第26卷第5期，受作者及月刊同意授權轉載。