【大宇宙小故事】28 麥加的方位
撰文|葉李華
根據伊斯蘭教的教規,信徒無論身在何處,每天都必須朝向麥加祈禱五次,而清真寺的建造也有嚴格規定,其中的米哈拉布(壁龕)一定要正對著麥加。
至於要如何確定麥加的方位,若是距離不遠,問題當然很簡單,只要攤開地圖,配合指南針即可。不過由於地球是圓的,如果距離拉大,就沒有那麼容易了。
●經緯線的差異
無論任何地圖,都是把地球表面的一部分轉移到平面上。如果是小區域,誤差就不會太大,正如把籃球剪成幾十片,每片都很容易壓成平面,雖然或多或少有些扭曲,但幾乎都可以忽略。然而,黃金時代的伊斯蘭世界幅員廣闊,涵蓋了北非、南歐、中亞與中東,想要把這些地區通通畫在一張地圖上,失真就在所難免了。
所以我們最好還是捨棄地圖,改用地球儀來研究這個問題。
先討論一個特例:如果某地和麥加在同一條子午線上,亦即兩地的經度相同,那麼問題同樣很簡單,因為麥加不是位於它的正南就是它的正北方。
可是,如果某地和麥加屬於同一條緯圈,也就是兩地的緯度相同,我們卻不能說「麥加不是在它的正東,就是在它的正西方」。
為什麼?因為想要定義方向,就要先定義直線,可是球面上當然沒有直線,所以只好退而求其次,用「距離最短的線段」來代替,而這些線段一定是「大圓」的一部分。我們曾經仔細討論過什麼是大圓,在此只做個簡單的複習:「經線都是大圓(的一半),緯線則幾乎都不是,只有赤道例外。」其餘細節請參考〈不假外求〉這篇文章。由於麥加並非位於赤道,通過它的緯線不是大圓,所以不能用來定義方向。
接下來,我們來研究一個有趣的問題:如果某地和麥加緯度相同(北緯21度25分),經度相差180度,那麼麥加是在它的東方?西方?南方?還是北方?
(如果看看地球儀,你會發現這個「某地」在夏威夷群島附近,姑且稱它為X島吧。)
正確答案是「正北方」!因為從X島坐飛機到麥加,最短的飛行距離是跨過北極,而不是繞過太平洋或大西洋,當然更不是繞過南冰洋。反之對於麥加而言,X島同樣在它的正北方,而不是正南方!有趣吧?
這就是所謂的「朝向問題」(qibla problem),它是個極具宗教色彩的球面幾何難題。在伊斯蘭世界的黃金時代,曾有許多學者研究過這個問題,其中最有名的當數比魯尼(Al-Biruni, 973-1048)這位波斯籍的全方位學者。
●地球的數學
在比魯尼那個時代,他的故鄉名義上是阿拉伯帝國的領土,實際上則是小國林立,頗為類似中國的春秋戰國。(雖然當時仍屬伊斯蘭黃金時代,但那純粹是指文化,而非政治環境。)
比魯尼一生經歷過兩個朝代:齊亞爾王朝、伽色尼王朝,這個改朝換代對他的學術生涯有著深遠影響。
一夕之間從地位崇高的學者變成高級階下囚,如果是平常人,很可能從此一蹶不振。但比魯尼卻能隨遇而安,繼續埋首研究各種學問。舉例而言,當伽色尼國王遠征印度北部,決定帶他同行,他不但欣然前往,還趁機對印度文化做了深入研究,開創了「印度學」這門學問。
總而言之,比魯尼是個全能學者,對於當時各種學問皆有所涉略,而且幾乎都有重大貢獻。想要在一篇短文中對他做全面介紹,注定會掛一漏萬,不如鎖定他在數學方面的重要成就,仔細探討一番。
無巧不巧,這些成就幾乎都和地球有關。
前面提到的「朝向問題」就是最好的例子,比魯尼發明了四種公式,每種都能讓你只要輸入所在地的經緯度,便能推算出麥加的方位。
在此所謂的經緯度,可想而知和我們現在使用的不盡相同。原因很簡單,當時還沒有格林威治天文台,所以經度當然不會以它為準。比方說,比魯尼所用的經度以加那利群島某處為零度(原因可遠溯至托勒密的著作),此外就和我們所熟悉的經緯度沒什麼差異了。
千萬別以為經緯度只有幾百年的歷史,事實上,早在公元前三世紀的古希臘時代,已經有學者提出經緯度的概念。這位學者不是別人,正是鼎鼎大名的埃氏(Eratosthenes)。我們在〈平的還是圓的〉這篇文章中介紹過他,強調他是第一位以正確方法測量地球周長的人。
在比魯尼之前,想要測量地球周長,唯有使用「埃氏法」一途。這個方法有個大缺點,就是要在兩個相隔甚遠的地點,同時測量太陽的仰角。比魯尼則發明了一個取代埃氏法的妙招,讓測量人員不必辛辛苦苦越過沙漠,只要爬上一座高山即可。
根據比魯尼的自述,他是在隨軍出征印度時想出這個方法的。當時他住在碉堡中,附近有一座高山與一片平原,某天他爬上那座高山,就突然有了靈感。雖然比魯尼的方法是測量地球的半徑,但只要乘以2π就是周長,請參考下圖(埃氏法放在旁邊以供對照)。

比魯尼只要在山頂量出α角,即可根據山高h算出地球半徑(∵cosα=r/r+h)。埃氏的方法則必須在兩個地點同時測量太陽的仰角,並量出兩地的距離差。
在這個方法中,最困難的部分是測量山頂的高度(其他的測量和計算都易如反掌),有些人以為比魯尼是使用大家在中學都學過的「三角測量法」,這種論斷犯了過度自信的謬誤。胡適曾說:「做學問要在不疑處有疑」,若是可疑之處,當然更要查證。
事實上,比魯尼甚至沒有用到量角器,而是使用一個「很大的正方形」當作測量工具。有趣的是,他測量山高的方法,正如他測量地球半徑,無須比較兩個地點的測量結果;只要找一個適當的地點,把正方形的傾斜角度調整成如圖所示(底邊和地面的夾角等於山頂的仰角),就能利用兩組相似三角形的比例關係(△HGC~△CEB, △HCB~△BAF),推算出山頂的高度。
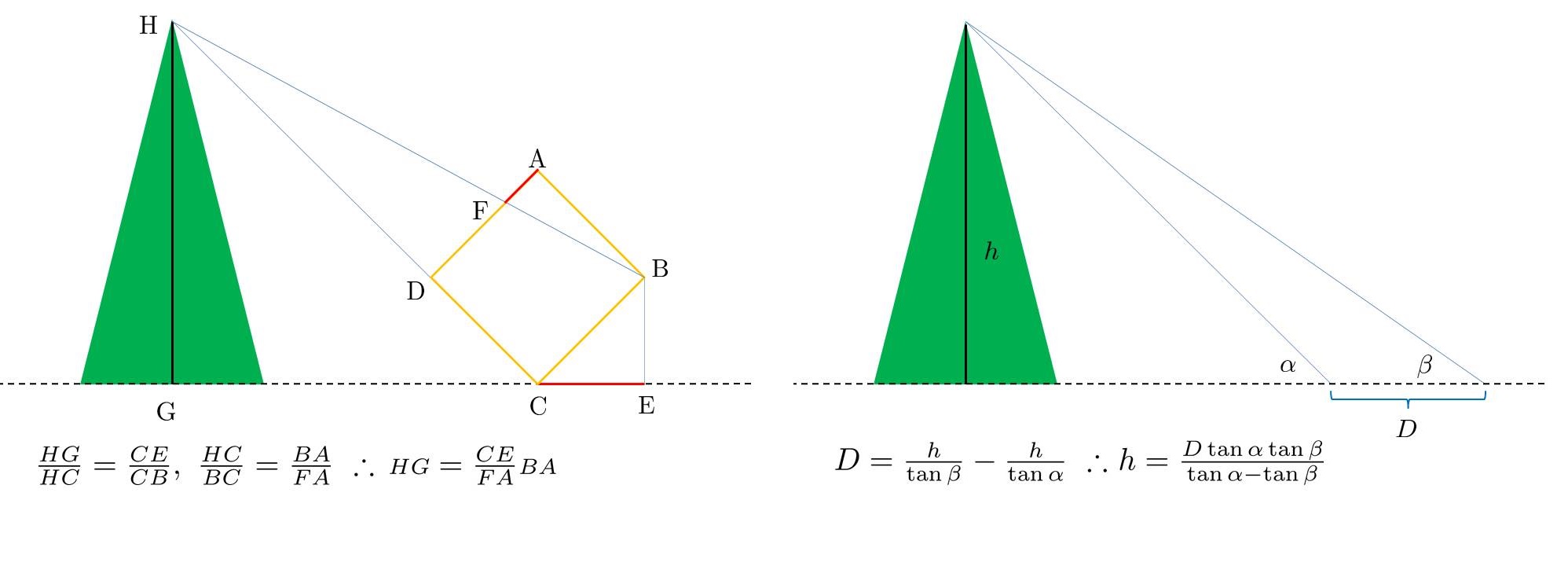
比魯尼只要在一處量出兩條紅色線段的長度(FA, CE),即可利用兩組三角形的相似關係算出山的高度(HG)。三角測量法則必須在兩個地點進行測量,並量出兩地的距離差。
●自我中心投影
一提到地圖投影,大家或許立刻會聯想到麥卡托。其實早在麥卡托出生前幾百年,比魯尼就發明了好幾種地圖投影法,其中最值得一提的是「(正)方位等距投影」(azimuthal equidistant projection)。如果你覺得這個名詞太專業,不妨改用「自我中心投影」這個戲稱。
通常的地圖投影是把地球儀想成半透明的球體,設法用燈光將其上的圖案照在紙上。可是「自我中心投影」的操作型定義和燈光或影子都毫無關係,而是一種標準的機械式操作,下面先用「以北極為中心」來做說明。
在桌上鋪一張紙,將地球儀倒置在紙面上,這時只有北極這一點和紙張接觸。假設這個地球儀剛剛出廠,上面的油墨還沒有乾,那個北極就會印在紙上,而我們就將它定為地圖的「中心」。
然後,讓地球儀在紙面上沿著某條直線滾動(只有滾動,完全沒有滑動)。在滾動過程中,雖然地球儀與紙張的接觸點不斷改變,但這些點通通屬於地球儀上的同一條經線。因此我們可以想像,這樣的滾動會把某條經線(連同其上的地形)印在紙張上。
如果將地球儀「歸零」,換一個方向來滾動,就會在紙上印出另一條經線上的地形。由此可知,只要將360度都滾過一遍,大致就能把北極附近的地形全部印在紙上了。

在這張地圖中,所有的經線都是通過中心點(北極)的直線,而所有的緯線都是同心圓。更重要的是,地球儀上各點和北極的距離在轉移到紙上之後完全沒變──因為是滾出來的,當然會有一一對應──這就是「等距」兩字的意義。
請注意,上面的論述只對北極這個中心點有效,對其他點就不保證等距了。
反過來說,在這樣的地圖上,從任何一點畫一條通過中心(北極)的直線,它必定對應於地球儀上的某條經線。這個結果雖然顯而易見,但如果將中心換成其他地點(例如麥加),就能從這樣的地圖得到非常有用的資訊。
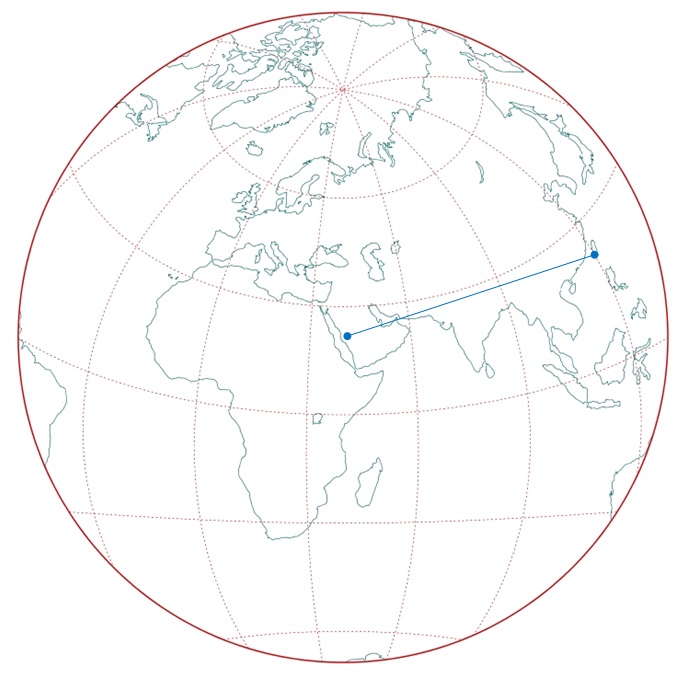
(作者繪,軟體來源:NASA: Global Map Projector, 麥加與恆春的連線為作者所加)
為了方便討論,讓我們以台灣的恆春為例(它和麥加的緯度幾乎相同,但我們已經說過,千萬別以為麥加位於恆春的正西方)。在這張地圖上,如果用直線連接恆春和麥加,就等於是在地球儀上用「大圓」連接這兩個地點,因此這個線段的長度就是地球儀上恆春和麥加的最短距離,而這個線段的方向,則是(在恆春人看來)麥加的正確方位。
比魯尼當初發明這種投影法,很可能是為了上述的第二個結果(正確方位)。但恐怕他做夢也想不到,第一個結果(最短距離)雖然是副產品,卻在幾百年後成了計算飛機油料的利器。
