【物理史中的五月】1618 年 5 月：克卜勒（Johannes Kepler）發現太陽系的泛音

1618 年 5 月：克卜勒（Johannes Kepler）發現太陽系的泛音

文｜蕭如珀、楊信男（臺灣大學物理學系）（譯自 APS News，2019 年 5 月）

中世紀與文藝復興時代的宇宙論皆由天體的「音樂宇宙」概念所主導，此隱喻很引人入勝，所以幾世紀來激勵了西歐大部分的藝術、音樂和文學。然而天文學家克卜勒（Johannes Kepler）在他 1619 年的專著《世界的和諧》（Harmonices Mundi）中奠下了一個更如實的天體音樂，他主張太陽系的星球在繞著太陽運行中譜出它們的音調。

1571 年 12月 27 日，克卜勒出生在德國現今司圖加特市（Stuttgart）的西邊。他祖父曾經是貴族鎮長，父親時家道中落，財富損失巨大，因此去當外國傭兵勉力維生，在克卜勒只有 5 歲時就棄家庭於不顧。母親是小旅店老闆，也是一位草藥商（此行業讓她幾年後被控告施行巫術）。克卜勒是一個體弱多病的小孩，但他數學優秀，從小便喜愛天文學。他 6 歲時，母親帶他去看 1577 年大彗星，他後來很生動地回憶起他九歲時第一次觀看月蝕，覺得那時月亮「看起來很紅」。

克卜勒曾罹患天花，病後視力不好，雙手殘廢，粉碎了當他離家去上杜賓根大學（University of Tübingen）時，想成為觀測天文學家的願望。但是他的數學能力卻好得讓他可以掌握星球的理論。他在學校學到了托勒密和哥白尼的宇宙論，擁護哥白尼的學說。雖然他原先希望成為神職人員，但他卻一畢業就在格拉茲（Graz）的一間學校當數學和天文學教師。

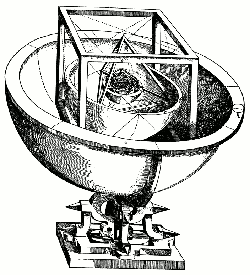
在格拉茲時，克卜勒受到土星和木星週期性會合的啟發，感受到像是天意一樣頓悟宇宙可能的幾何基礎。他於是創造了一個模型，其中 5 個柏拉圖立體（正多面體）都裝進一個球體內；假如把它們彼此套疊，可以得到 6 層，剛好對應當時已知的 6 個行星（水星、金星、地球、火星、木星和土星）。他將此結論收錄在他的第一本天文著作《宇宙的奧秘》（Mysterium Cosmographicum）中，1596 年出版，當時他年僅 25 歲。

雖然該書有一些錯誤，但還是引起知名的天文學家，包括第谷‧布哈赫（Tycho Brahe）和尤色斯（Reimarus Ursus）的注意。布哈赫和克卜勒有許多書信往來，信中布哈赫嚴詞批評這位年輕天文學家的研究，包括克卜勒依賴哥白尼不精確的數據。1600 年，克卜勒到布拉格附近正在新蓋的天文台拜訪布哈赫，慢慢地得到布哈赫的信任，可以使用他更精確的資料。克卜勒後來搬到布拉格，當布哈赫的助手，當布哈赫過世後，便繼任他為皇家數學師。

那時，克卜勒對數學、音樂和物理世界之間的數字關係產生興趣，開始這方面的研究，再次利用幾何呈現他的概念。他相信幾何「提供造物者裝扮全世界的模型」，也希望以音樂來表示此和諧──一個哥白尼太陽系的「天體音樂」，正如托勒密在《諧音》（Harmonics）中一樣。（和克卜勒同時期的弗拉德，Robert Fludd，也發展出和諧理論，兩人為此激烈爭辯。）

行星和太陽最大和最小的距離並沒依循調合比，但克卜勒推論說，行星運轉最快（收斂運動）與最慢（發散運動）的位置也許更適合與合諧律動做類比。

因此，舉例來說，土星最大與最小角速率的差別符合 4:5 的比例，對應於音程中的大三度，而木星的差別是 5:6 的比例，或是小三度。火星是 2:3，金星是 24:25，地球則是 15:16。克卜勒解釋這小和諧音階的理由：「地球唱著 Mi, Fa, Mi，你甚至可以從音節推論，在這裏，苦難（misery）〔Mi〕以及飢荒（famine）〔Fa〕一直都在我們家鄉的生活中」。克卜勒主張說，行星很難完全和諧地合唱，也許只有在宇宙創造的那一刻才會發生。

火星和土星的收斂與發散運動的比例是不符合和諧模式的唯二音程，產生了 18:19 的不和諧比例（小行星帶直到 1801 年才發現，因此並不計入克卜勒的計算中）。雖然如此，此研究還是成了克卜勒《世界的和諧》（Harmonices Mundi）一書的基礎，1619 年出版。書中第五和最後一章說明他發現行星的和諧運動。

最終，此研究成了克卜勒第三定律，說明行星各自的軌道週期與它們和太陽距離的關係，一般的定義如下：行星繞恆星公轉之週期的平方與行星到恆星之平均距離的立方成正比（至於第一和第二定律，克卜勒在他前一本書《新天文學》，Astronomia Nova，中有詳細闡述）。在 1660 年代，克卜勒第三定律（和惠更斯，Christiaan Huygen，的離心力定理）幫助牛頓和哈雷證明了太陽和它的行星之間萬有引力的平方反比定律。