投資學、核物理與隨機矩陣（二）

撰文｜蕭維翰

在前文中筆者嘗試說服讀者，投資的策略是可以利用數學去優化的。但即便只針對隨機過程，依舊有太多工具可以選擇。本系列文將側重於隨機矩陣這個例子，日後有機會再聊聊其他的工具。而選擇隨機矩陣的原因乃在於這個數學分支一部分的重要貢獻來自於核物理的研究。

在本文中，我們將回顧隨機矩陣在核物理發展中產生的助力，並在下篇拉回近代，說明這些想法怎麼被使用到財務問題中。

時間拉回到 1950 年代，物理學家們在核物理的實驗中觀察到許多光譜線。這裡的光譜線的概念和高中化學的氫原子光譜是一樣的。簡而言之，薛丁格方程式會決定一個系統（比如說氫原子）允許具備的穩定狀態與這個狀態具備的能量有哪些，當系統從一個狀態跳到另一個狀態，兩狀態之間的能量差以電磁波的方式釋放並被實驗觀察到，便是光譜。

實驗上，對於光譜的了解有助於我們回推一個系統可能具備的結構。（譬如當初庖立（W. Pauli ）便是從茫茫光譜之中了解並提出了庖立不相容原理，這種觀察力直到今日依舊犀利得可怕。）

但人們對於當時從慢中子共振實驗蒐集到的釷 232、鈾 238 光譜，一時間其實沒有太好的分析點子。核子內的能量結構一直是很錯綜複雜的。尤其在慢中子的實驗中，如果入射中子的能量解析度不是很高，它將不會只激發其中一個或兩個能階 — 反之，一次就會有一大堆能階被激發。也因此，部分的精力就被集中在研究光譜線的統計性質上。

那好，我們是不是就坐下乖乖地解薛丁格方程式，然後對它們的能譜進行統計分析就好了呢？很可惜，別說一般性的薛丁格方程複雜得無從解起，在這類核物理的問題中，我們甚至不知道精確的微觀物理有哪些要素。

面對這種無從著手的問題，著名數學物理學家 F. Dyson 當時的點子是 — 那我就考慮一些一般性的矩陣，而這些矩陣的元素都是隨機變數，唯一的物理限制來自於物理模型應該具備的對稱性。在群論中，具有不同對稱性的矩陣們會被分類到不同堆。由於這種考慮的一般性，如果有任何結論可以被推導出來，那麼這些結論雖然無法告訴我們最微觀的細節，但統計性的結論應該要可以適用到所有具備這樣對稱性的模型內。

這種陳述，對日常生活而言，還是有點抽象。讓我們更具體一點來看一個當時人們嘗試回答的問題。

如前言所述，我們在研究光譜線。乍看之下，實驗中得到的光譜線的位置分佈並沒有什麼規律。統計上一個可以問的問題是，不同線之間的距離是怎麼分佈的。白話（約略）一點說，如果我在能量 E 的地方有一條光譜線，那麼距離這個點 S 單位能量內都沒有另外一條光譜線的機率 是多少？

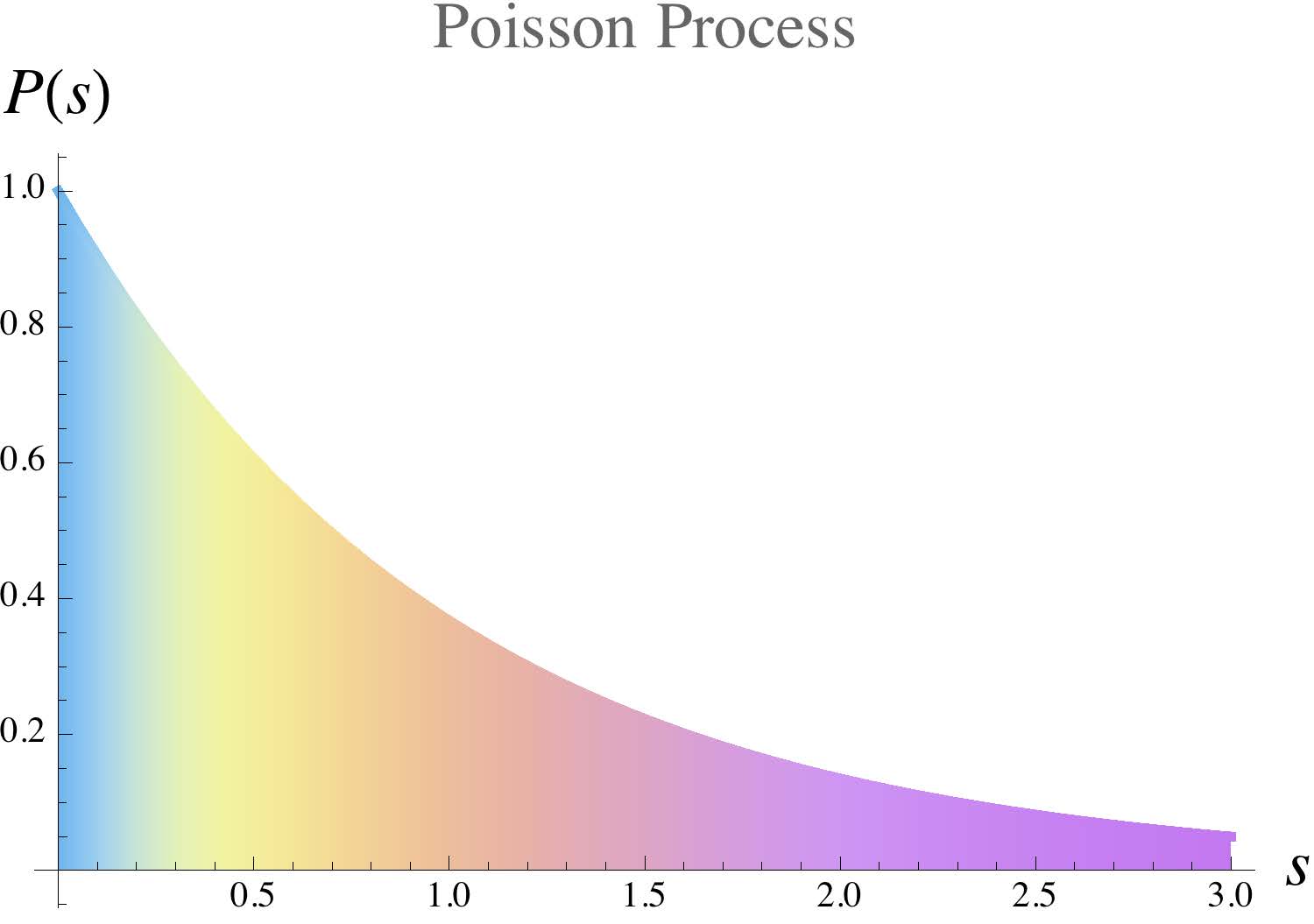
倘若我們假設不同能階之間是沒有統計上的關聯的，那麼有上過三類組的大一微積分（或不小心學了大學部的機率與統計）的讀者們會發現這是個 Poisson 過程。具體是什麼也不那麼重要，重點是它已經被這個法國人解了，所以我們知道答案的長相，如圖一。

但可惜，如果我們把 Poisson 過程的解拿去與實驗統計的數字比對，實在相去甚遠。但至少我們從中得到了一個結論：至少在具有相同量子數的那堆能階間，它們是有統計關聯的，那麼下一個問題就是，有沒有一個簡單好懂的模型讓我們懂這個關聯？

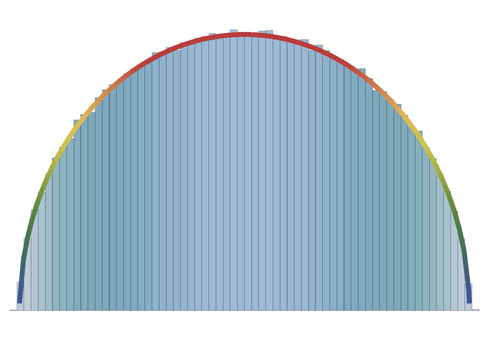
筆者所知道最簡單的例子是所謂的高斯系綜（Gaussian ensemble），而在諸多高斯系綜中，最簡單的例子是高斯正交系綜（Gaussian orthogonal ensemble，GOE）。讀者完全不用去追究這些單字的意思，這類矩陣的意思是，有一堆實數對稱矩陣，它們的矩陣元素由常態分佈給出。實數、對稱矩陣、跟常態分佈，整個難度一下回到了高三數學。僅僅分析這類矩陣的能譜就還滿有趣的，譬如它們的能譜分佈會被侷限在一個半圓之中（見圖零），這也是有名的半圓律（semi-circle law）。

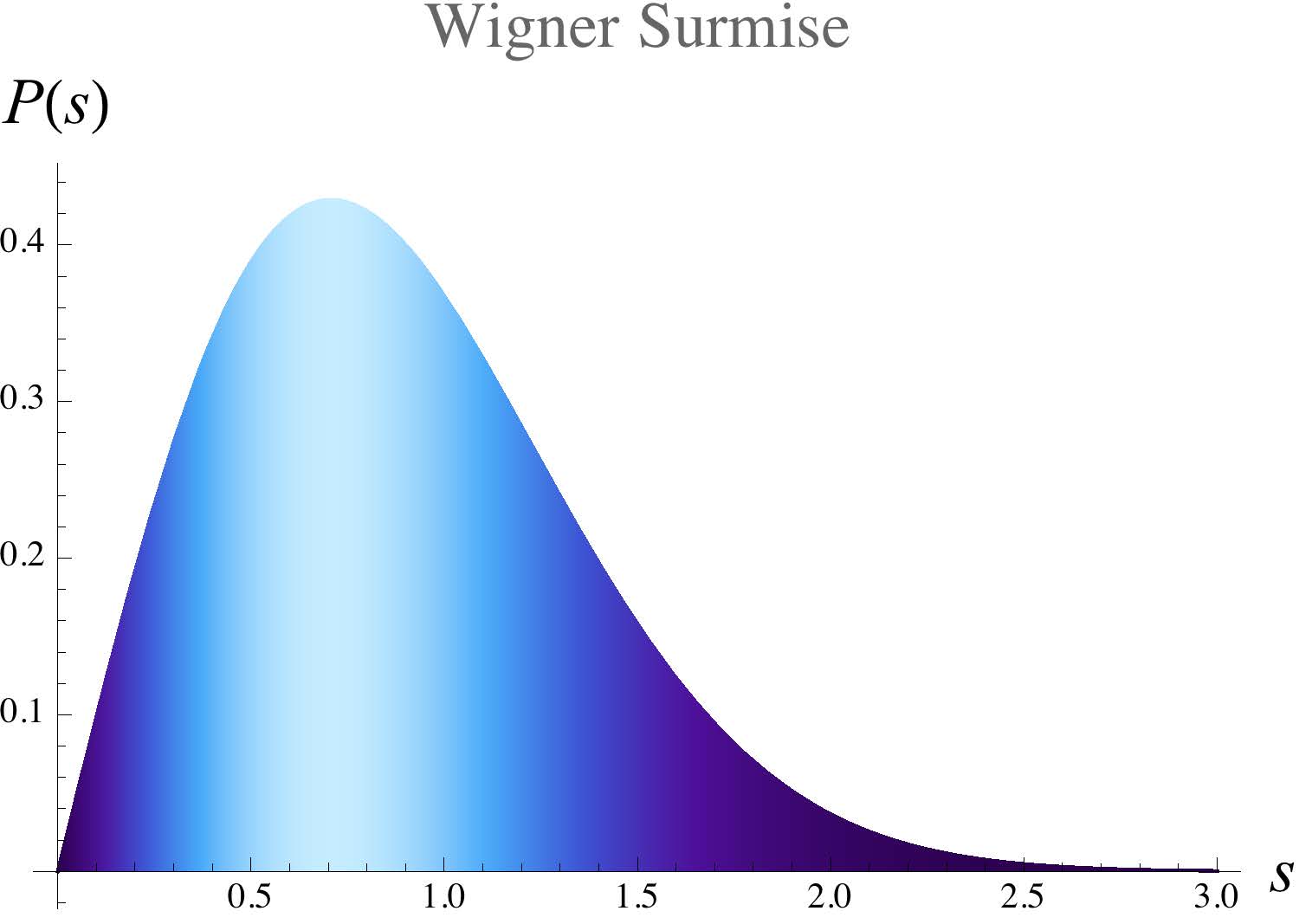
1951 年，透過對幾個簡單的高斯系綜的計算，物理學家 E. Wigner 提出了著名的 Wigner surmise ，並推測了前述的  應該有的形式— 並不是 Poisson 過程，而是如圖二所示。值得注意的是，這個新的分佈在原點為零： ，意指了兩個能階間會避免交會，這種現象是量子系統的一個特徵。

近 70 年後的今日回顧這段歷史其實還頗有趣的。由後來的統計分析，我們得知沒有任何一種高斯系綜可以完美符合核物理光譜的能隙分佈，另一方面，當我們真的用高斯正交系綜進行計算，Wigner surmise 也只準確到大概 95% 的程度。（不過以猜答案的觀點來說，在定量上這已經準確得駭人了。） 然而這些研究在隨機矩陣的發展依舊起了根本性的衝擊。緊接著在下一篇，我將跟大家分享這種分析手法如何被應用在瞭解金融數據的問題上。

 

參考資料：
[1] M. L. Mehta, Random Matrices (2004).
[2] E. Wigner, Ann. Math. 53, 36 (1951).
[3] E. Wigner, Random Matrices in Physics, SIAM Review, Vol. 9, No. 1 (1967).
[4] T. Guhr, Random Matrix Theory in Physics

 

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。