投資學、核物理與隨機矩陣（一）

■物理學中的這些「奇技淫巧」真的只能拿來研究大自然嗎？事實上它們可能比我們想像的有用。

撰文｜蕭維翰

近二三十年來有一個新起的學門叫做經濟物理（Econophysics）十之八九的人一聽到這個名字，大概會皺起眉頭詢問這兩個學科有什麼關係。從日常柴米油鹽的角度，這兩個社群固然是風馬牛不相及，但從定量科學的角度—

都是算數學，沒有什麼太大的差別。

當然不同社群的研究者切入問題的角度跟直覺都相去甚遠，但也部份地基於這個原因，經濟物理便著力於使用物理學中攻擊複雜系統的技巧來處理財金問題，近年來也有越來越多的財務著作發表在物理學評論 E （physical review E）或物理學評論通訊（physical review letter）。

不侷限於物理學的窠臼。事實上在許多定量科學的研究中，有一些行為是很一致的。我們常先有一些對於實務的觀察，接著我們嘗試把這些觀察抽象化成一些數學模型，並且從這些數學模型去得到預測性的結果。在物理學中這個預測可能是未來某個實驗會觀測到的現象，在財務上，這個預測就是我們應該要採取的處理錢財的策略。

但筆者必須指出一點財務問題與常見物理問題的不同之處。

電子不會因為你知道了薛丁格方程，它就賭氣不再遵守薛丁格方程式了。當你找出一個遊戲規則，在物理學中你就可以重複地應用它。但財務問題不同，當你找到一個很好的賺錢策略，然後大家一窩蜂地遵循這個策略，供需平衡的結果就會讓這個優勢失效，然後我們就得再回家做功課。

讓我們轉回到財務問題。在眾多財務問題中，其中一個很直覺的主題就是投資。這個問題之所以普世，是因為它的規模可大可小，從兒童們對壓歲錢的消費、上班族對薪水的支用，到基金經理人對資本的分配，在生命中不同時刻我們一直進行著如何進行投資選擇的問題。

若我們考慮所有可能的投資選項：包括債券、股票、選擇權及其他衍生性商品，那投資其實跟賭博沒有兩樣。意思是—不要過於相信自己（的直覺），要相信數學。

這時我們就可以檢視一下我們對於金錢有哪些很普世的直覺。

譬如：「不要將雞蛋放在同一個籃子裡。」這句話是一種感覺，抑或有定量上的結果？我們可以考慮下面簡單的情境。譬如有兩個商品 A 跟 B，從時間 1 到時間 2 ，A 上漲了 100% 而 B 跌了 50%，從時間 2 到時間 3，A 下跌了 50% 而 B 漲了 100%。若你有 100 單位的資本，全部投注在 A 或 B 上，則在時間 3，你不賺不賠。

但如果在時間 1 你將 50 單位給 A ，另外 50 單位給 B，在時間 2 時，你擁有 125 單位。然後你再重新分配，將 62.5 單位給 A 並將 62.5 單位給 B，則在時間 3 時，你會得到淨利。所以在某些狀況下，不要把雞蛋放在同一個籃子似乎有點道理。

再譬如：「利潤愈大，風險愈高。」這句話只是我們正常人的迷思，還是數學上也為真？在回答這個問題之前，我們必須先想辦法在數學上定義「風險」（risk）才能把這個因素放進模型裡做計算。

然而就我所知，就連這件我們以為很有直覺的事情都不一定有很普世的數學定義。

近代關於投資策略的理論是由 Markowitz 建立的。在他的模型中，給定金融商品的統計資訊，我們可以計算某一組投資組合的平均報酬，同時也能計算這個組合的標準差，在這個平均-變異數模型內，變異數或它的平方根，標準差，被當成了量化風險的一個指標。統計上的意義就是，如果標準差極小，那我的報酬就有很大的機率會是我計算的平均。（當然也可以用高中學的信心水準作更精確的陳述。）

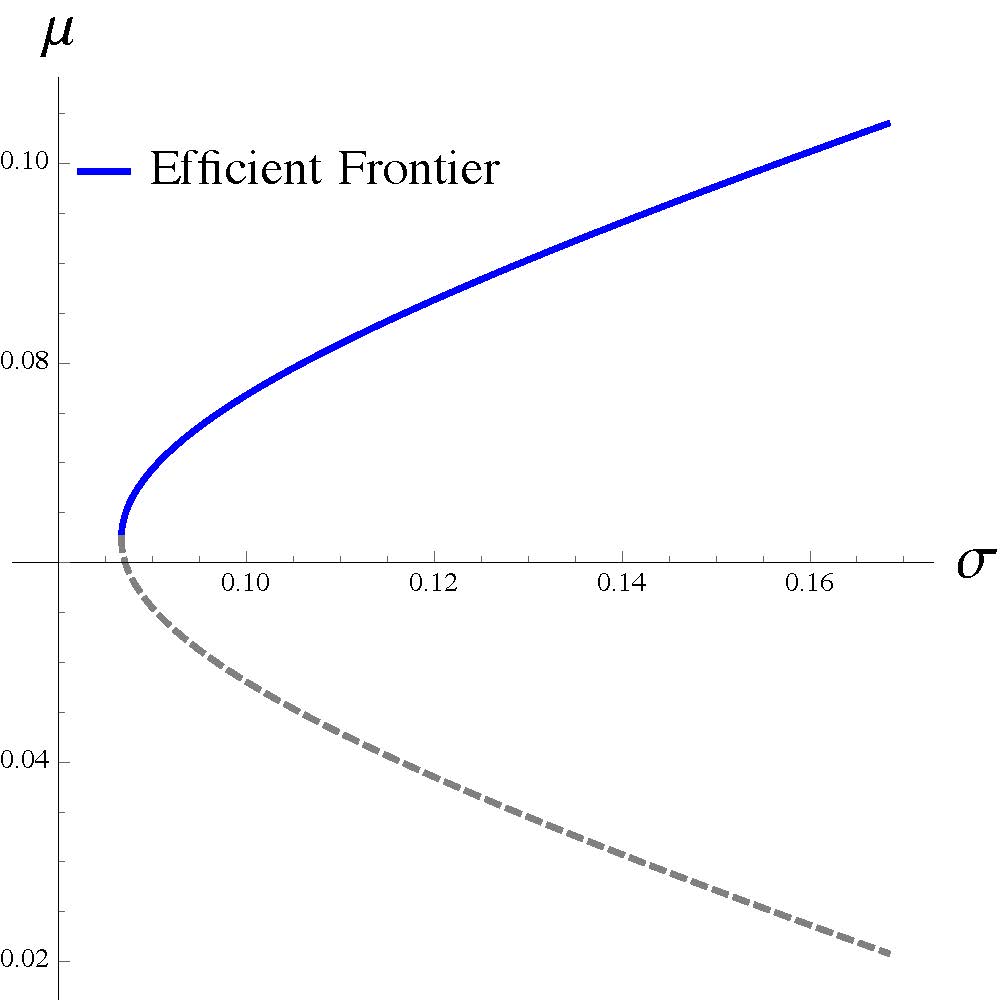
有了這些量化的定義，我們便可以嘗試回答是不是利潤越高風險越大。在最簡單的 (i) 固定總資本並 (ii) 沒有無風險資產的模型中，根據「對風險的容忍度」，我們其實有辦法在報酬和風險的平面上畫出一條「效率邊界」（efficient frontier）這條線，這條線代表我們在這個模型中最有效率的玩法，也就是給定風險時，此線給出的期望報酬最高，而固定期望報酬時，此線上的點具有的風險最低。而且該邊界的走向也是還符合一開始的直覺—追求更大的利潤，就要承擔更大的風險。

回到前面問題的敘述，要計算平均與變異數需要金融商品，比如說道瓊指數前 100 大的股票，的價格等訊息。實務上這些資訊可以透過公開的交易紀錄獲得—而一個很自然的問題就是，這些金融商品的統計關聯性是不是有跡可循？

在下文中，筆者將為大家介紹在物理學中也曾經有一些問題需要分析雜亂無章的矩陣資訊，而這個光譜問題，促發了隨機矩陣理論的發展，更後來的學者們，更將這個技術轉移到了金融商品資訊的分析上。

 

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。