路徑積分與費曼圖（上）

撰文｜蕭維翰

本次費曼專題筆者希望透過兩篇文章談論費曼的路徑積分與費曼圖，作為費曼科學工作的代表。而本文將側重於路徑積分，並在結尾引出費曼圖。

但在科學開始之前，筆者必須承認，一直以來，我認為談論費曼的科學工作不是簡單的事。困難處不在於那些科學技術上的深澀，反在於它們的基礎性與普世性，在沒有獨樹一幟的新見解前，這個世界需不需要多一篇介紹費曼學術成就的科普文？

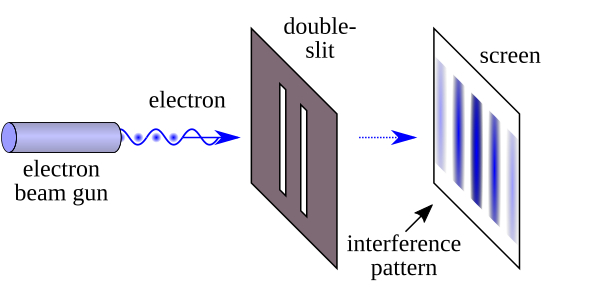
筆者相信在 CASE 的多年耕耘下，讀者們對於路徑積分或多或少都有所耳聞。科普界亦已有許多談論路徑積分的文章，絕大多數都會以光子或電子的雙狹縫干涉實驗為物理動機進行說明，以一個科學工作者的角度來看，這的確不失為好的介紹方式——首先提出實驗可想見實現的物理情境，接著嘗試利用物理直覺猜測可能的結果，再以意料之外的真實現象誘使讀者思考，最後說明迄今人類對於此問題的理解，並抽象化成為整個量子理論的指導原則。

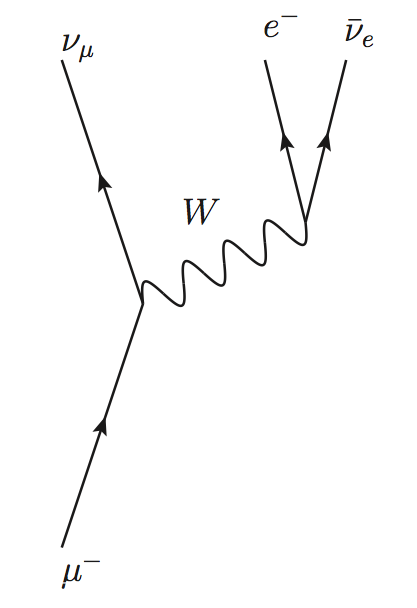
也因此，本文意欲規避上述的結構，一來降低以路徑積分為題的科普文章的同質性，二來筆者也沒有十足的信心能給出比費曼本人在《費曼物理學講義》中更好的詮釋 [1]。

為了走得更遠一些，我們從此處出發：在量子力學的框架下我們被允許去問，從一個量子態 I 到另一個量子態 F 的躍遷振幅，這個躍遷振幅的絕對值平方是從量子態 I 到量子態 F 的（古典）機率。設想在 I 與 F 間會有一些可能的中間態 m，量子力學的原則指出，倘若將 I 到 m 間的振幅，乘以 m 到 F 間的振幅，再加總所有可能的中間態，會得到原來欲求的 I 到 F 振幅。（在古典機率論則是將上述的振幅替代為機率，二者間的差異則是所謂的量子干涉。）

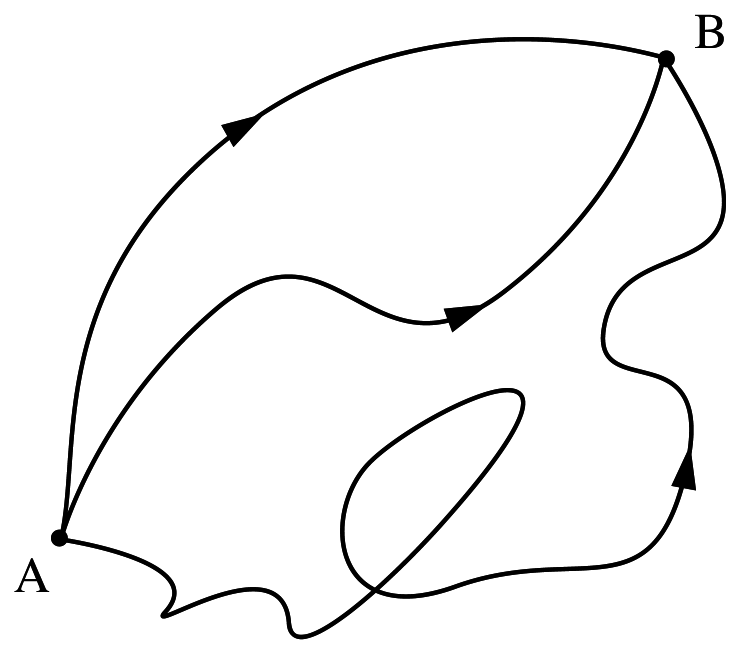
若將前述的原則套用到一個粒子在空間中兩點間的躍遷，那麼我們就必須考量連接這兩點的所有可能路徑，再為每條路徑計算一個振幅，最後進行加權平均，「路徑積分」便是費曼給我們關於每條「路徑」對應的振幅以及最後加總應該怎麼計算的「答案」。

費曼也在其名篇中 [2] 演示，路徑積分與海森堡矩陣力學和薛丁格波動力學之間的等價性。或許有讀者會懷疑，既然三者所描述的量子力學都是「等價」的，學者們究竟有什麼理由學盡所有，而非專精其一呢？

從概念的觀點切入，在矩陣力學、波動力學的框架下，我們幾乎被迫放棄一些古典上直觀的概念——譬如粒子運動的軌跡，路徑積分雖然也是計算狀態間的躍遷機率，但隱約地允許我們移植「路徑」的概念。並且在古典極限下，路徑積分也能說明為什麼古典粒子會遵循古典軌跡。

從計算的角度著手，前揭的三種方法各擅勝場。讓我們說得更具體些，在現有量子力學中的框架內，有哪些是可以計算的呢？從解釋實驗所見的觀點，為了說明光譜的頻率與強度，讀者們可能會合理期待，經過一世紀多的研究，量子力學至少要可以計算原子內的能階與系統在不同能階之間躍遷的機率。大學部程度的量子力學即將絕大多數的心力集中在波動力學，亦即透過研究薛丁格方程式來計算簡單系統中允許的能階。

路徑積分可以計算自由粒子與量子簡諧運動的躍遷振幅，然而，對於絕大多數的系統，比如氫原子模型，利用路徑積分計算波函數與能階顯然是一個吃力不討好的方法 [3]。

稍稍出人意表的是，當問題升級為計算複雜度更高的量子場論，相對於傳統的矩陣力學與波動力學，透過路徑積分來量子化一個理論，卻顯得相對簡單。在許多問題中，當我們寫下一個模型，即可以透過模型的結構推導出費曼規則（Feynman Rules）。費曼規則就像是樂高積木，為每一個物理過程的小單元指定一個代數公式或運算法則。我們可以將複雜的物理過程拆解為基本單元的組合，然後透過費曼規則去得知複雜物理過程的躍遷振幅。

而用一些簡單的圖像表達物理過程，即是所謂的費曼圖。

在下文中，筆者將繼續說明一些路徑積分的用處，以及介紹一些簡單的費曼圖，希望能讓讀者感受到它們的巧妙。

 參考資料：

[1] R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman lectures on Physics, Vol. 3 (1964).

[2] R. P. Feynman, Space-Time Approach to Non-Relativistic Quantum Mechanics, Rev. Mod. Phys., 20, 367 (1948).

[3] I. H. Duru, and H. Kleinert, Quantum Mechanics of H-Atom from Path Integrals, Fortschritte der Physik 30, 401 (1982).