【大宇宙小故事】44 有沒有故事(上)
撰文|葉李華
想必大家都知道,世上第一部成文憲法是制定於1787年的美國憲法。
任何一部憲法都不可能完美無缺,美國憲法當然也不例外。但是美國人在修憲時,絕對不會更動憲法本文,而是一律以「修正案」的方式附在後面。換句話說,直到今天為止,美國憲法的本文仍舊維持230年前的樣貌。
兩百多年下來,這類修正案總共累積了27條(而已)。最有名的是前十條,統稱為「權利法案」,它幾乎和憲法本文同時生效。
其餘的修正案有好幾條和選舉權有關。例如第15條讓所有的美國男性都享有選舉權,時間是南北戰爭結束後不久,兩者的關聯十分明顯。至於美國女性,直到1920年才終於爭取到這項權利(憲法修正案第19條),這在今天看來實在難以想像。而將投票年齡從21歲降為18歲,則是相當晚近的事(1971年第26條修正案生效之後)。
至於美國總統只能連任一次,原本一直只是慣例(因為華盛頓做完兩任便告老還鄉),所以小羅斯福的特例(做了十三年後死於任上)在當時並不算違憲。羅斯福總統逝世六年後,第22條修正案才明文規定以兩任為限。
在這些修正案中,最有趣的莫過於18與21這兩條,前者(1919年)就是俗稱的禁酒令,後者(1933年)則宣布將它廢除。由此可知,在美國憲法史上,沒有任何事務能夠一筆勾銷;無論多麼睿智或愚昧的立法,都會在歷史上留下永久的記錄。
總而言之,這是一部充滿故事的憲法。正因為有故事,在研讀這樣的憲法時,不會令人感到枯燥無味。
那麼其他國家呢?比方說,當今的法國已經進入第五共和,前面四個共和是怎麼來的,又是怎麼結束的,背後應該有不少故事吧。可惜的是,那些故事並未寫進第五共和憲法中,如果你感到好奇,必須自己設法在別處尋找。
同理,介紹科學知識的方式大致也有兩種,不妨稱之為「美國(憲法)式」和「法國(憲法)式」。「美國式」的優點是引人入勝,缺點則是難免有點囉嗦,讀者如果只想瞭解科學知識,必須從故事中沙裡淘金。反之,「法國式」的優缺點則剛好相反。
這麼說難免流於空泛,不如秉持科學精神,好好做一次實驗。
* * *
在上百種原子中,氫原子是最簡單的一種,它的原子核就是一個帶正電的質子,而原子核外面只有一個電子。
根據古典物理學,這個電子繞著原子核作圓周運動,有點像是月球環繞地球公轉。不同的是,月球和地球的距離幾乎固定不變,電子和氫原子核則是可近可遠──兩者距離越遠,電子的總能量(動能+位能)也就越大。
科學家很早就知道,在原子那麼小的尺度下,古典物理經常會失靈。因此想要正確描述氫原子,必須用量子物理取而代之。一旦改用量子物理,電子的總能量就會被「量子化」,換言之變成離散值,不過「距離原子核越遠總能量越大」的趨勢仍然保留了下來。
我們不難為這樣的系統找到實際的類比,例如圓形劇場就很合適(請注意這只是比喻,不太可能完美對應)。如果把中央舞台當作氫原子核,電子就是劇場中唯一的觀眾。既然觀眾席上沒有第二個人,他可以隨意坐在任何一個位子上。

如果選擇靠近舞台的位子,他的位能自然比較低,反之坐得越高,位能就越大。由於兩階之間沒有任何座位,階梯的編號剛好可以描述位能的大小,而這些位能當然是不連續的。
至於在氫原子中,電子的總能量是以「量子數」來編號(n=1,2,3...),它和圓形劇場的階梯在概念上非常類似,因此通常稱為氫原子的「能階」。
前面說過,既然整個劇場只有一名觀眾,他可以隨意選擇自己的座位。同理,氫原子中的那個電子可以待在任何一個能階。能階越高,量子數就越大,電子距離原子核也就越遠。
由於每個能階的能量都不一樣,電子若想換到另一個能階,一定會伴隨能量的轉移。如果是降級,電子會放出若干能量;如果是升級,當然需要先獲得能量。對於原子中的電子而言,它只能釋放或吸收電磁波的能量,其他的能量都敬謝不敏。不過既然這是量子物理,你不妨在心中將上述的「電磁波」代換成「光子」。
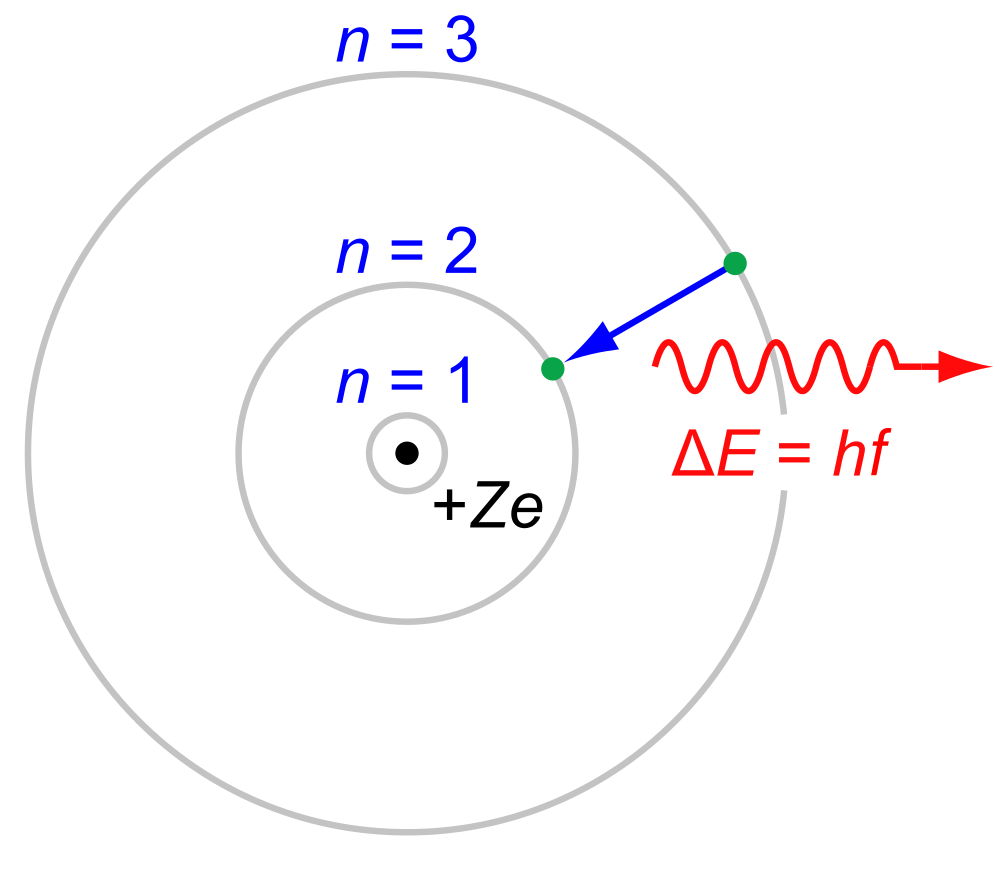
講到這裡,終於可以和實驗扯上關係了。
氫原子是標準的微觀系統,但如果有許多氫原子(例如一莫耳)同時吸收或釋放電磁波,便會產生很明顯的巨觀效應。研究這種巨觀效應的學問,通稱為「光譜學」。
一提到光譜學,或許你就會聯想到「吸收光譜」和「發射光譜」。請注意,在此的「吸收」和「發射」都是指上述的電磁波,因此吸收光譜就是電子升級的證據,反之發射光譜則對應於電子降級。
在光譜學中,氫原子的發射光譜可細分為幾個系列,各系列都包含無數條離散的「亮線」,卻沒有任何連續的「亮帶」。因此我們可以說,這個光譜就是氫原子具有離散能階的定性證據。
依照慣例,這些系列都以人名來命名,例如來曼系列(Lyman series)對應於電子從某個較高的能階降級到最低階(n=1);巴耳末系列(Balmer series)對應於降到第二階。此外還有帕申系列、布拉格系列、蒲芬德系列以及韓福瑞系列,分別對應於電子從高能階降到第三、四、五、六階。
來曼系列的譜線全部是紫外線,巴耳末系列的譜線包括可見光和紫外線兩者,其他系列的譜線則一律是紅外線。
其中巴耳末系列最有趣,它的前四條譜線落在可見光的範圍,其餘各條由於波長小於400奈米,根據定義都是紫外線。可是,可見光和紫外線的分界其實沒有那麼明確,一般人仍可用肉眼看見本系列的第五與第六條(波長分別為397.0以及388.9奈米)。

不過,千萬別以為光譜只能提供定性的證據。事實上,光譜實驗的數據通常都很精確,足以作為氫原子能階的定量證據。下面做個簡單的示範:
氫原子能階的公式是:En=-2.180*10-18/n2焦耳
如果電子降級,量子數從n降到m,釋出的能量是△E=2.180*10-18(1/m2-1/n2)焦耳
這個能量如果轉化成一個光子,那麼根據愛因斯坦的理論(光子能量=普朗克常數*頻率),我們就能輕易算出對應的電磁波其頻率和波長。用巴耳末系列的第五條譜線為例,它對應於電子從第七個能階降級到第二階:
△E=2.180*10-18(1/22-1/72)=5.005*10-19焦耳
頻率=△E/h=5.005*10-19/6.626*10-34=7.553*1014/秒 (其中h是普朗克常數)
波長=光速/頻率=299792458*109/7.553*1014=396.9奈米≒397.0奈米
我們之所以相信氫原子能階確實存在,正是因為有這些精確的光譜數據作後盾!
* * *
如果你覺得上文簡潔有力,或許意味著「法國式科普」很適合你。但如果你覺得少了些什麼,沒關係,我們的實驗尚未結束。
附錄:芮得柏公式(Rydberg formula)
本文範例中的三個計算步驟,其實大可合併為一個式子:
波長=光速/頻率=光速*h/△E=91.13/(1/22-1/72)奈米
這個式子當然可以推廣成「電子從第n階降到第m階」的一般情形:
波長=91.13/(1/m2-1/n2)奈米
這就是所謂的芮得柏公式,不過更常見的版本是:
1/波長=R(1/m2-1/n2)
其中R=0.01097(單位為奈米的倒數)=1.097*107(單位為公尺的倒數)
