【探索15-8】混沌裡有一隻黑天鵝
講師｜師大物理系 陳啟明教授
撰文｜陳奕廷
在一個根深蒂固地相信世上只有白天鵝的社會中，若飛入一隻黑天鵝，這個社會將會如何被撼動呢？「黑天鵝」除了象徵非常脆弱的思想體系，在經濟學中，也代表著極為罕見卻有深刻影響的事件。歷史上幾次經濟泡沫都被稱為黑天鵝，其對社會的影響在教科書上皆有描述。但是，究竟黑天鵝為什麼會出現，才是人們真正感興趣的對象。
●古典的研究方法
物理學美妙的地方在於它能將日常生活中看到的千百種看似不同的現象抽絲剝繭，釐清背後主導這些現象的真正原因。誰能知道太陽每天升起和蘋果從手上掉下，背後竟能由相同的理論來描述。傳統物理學解決問題的方法是先用『還原法』找出形成系統的最小單位，將問題簡化。隨後，再用『隔離法』拋棄不必要的變因並留下真正關鍵的因素。如此一來，我們方能用最簡單的方法描述物理世界的運行，就像我們能用相同的運動定律來描述蘋果和橘子從手上掉下來的過程，而不用分別為蘋果和橘子創造出兩種不同的運動定律。
能透過研究系統最小單位來研究系統的變化，全都有賴於「線性」。以下這則故事可以幫助我們了解何謂線性：
「禮拜一小明上課睡覺，老師扣他操性2分。禮拜二小明沒寫作業，老師扣他操性5分。禮拜三小明暨沒有寫作業，上課又睡覺。」
如果老師-小明這個系統是線性的，我們可以大膽預測禮拜三老師將扣他2+5=7分。我們在研究一個線性系統時，能先研究系統的小部分，再將其結果疊加成整個系統的答案。相反的，如果老師在禮拜三一氣之下扣了小明10分，我們可以說這個系統是非線性的。
●當混沌遇上經濟學
系統中單一因子通常可以用線性理論來描述，因此諸多物理定律都是假設因子間無交互作用或是交互作用很弱，並用線性的方式呈現。但是在現實生活中有許多系統，我們若將交互作用忽略則無法完整描述它們。在本季探索講座中探討到描述天氣的勞倫茲方程組、動物身上的斑紋以及昆蟲的群聚現象，都需要非線性的渾沌理論才得以較完整地被解釋。然而，這些研究仍侷限在物質及生命科學的範疇。近來，科學家積極地將相同的理論應用在社會科學中。由於經濟學中人與人之間的經濟行為是不可或缺的，以物理學的語言來說，這是一個強交互作用的系統，並難以使用『還原法』來研究它。此外，在研究經濟學時，鮮少能像研究物質科學一樣透過固定控制變因來決定單一因素對系統的影響，『隔離法』也不能很好地適用。這正是同樣使用這兩個方法的古典經濟學有時會失效及黑天鵝出現的原因。由此可見，若要由物理學的觀點研究經濟學，必須使用非線性的模型，而我們稱這樣的方法為『混沌經濟學』。
以股票為例，假設一支股票在時間 
的價格為 
，其價格會因需求而以比率r成長。當價格達到 時，賣家會賣出股票，同時股票會下跌 
。在這樣的模型之下，股票的價格可以用本季第2次講座中提到的混沌模型來描述：
其得到的結果能大略地解釋股票價格的震盪。
●換個角度看混沌
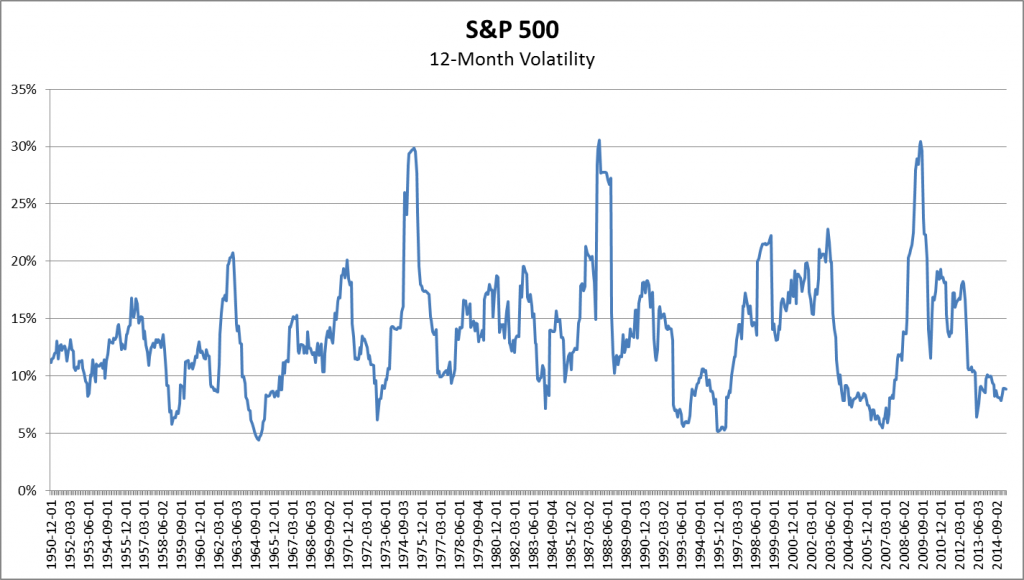
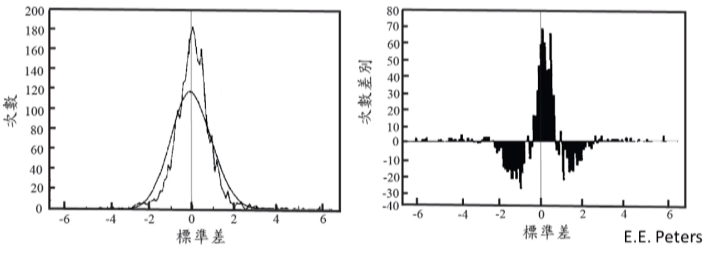
透過統計能看出另一個混沌經濟學能適用的原因。圖一顯示1950到2014年間S&P500指數的變化，乍看之下其震盪看似一個隨機過程。儘管隨機過程和混沌過程都具有不可預測性，只有後者具有決定性(determinism)。圖二比較隨機過程和S&P500指數的統計，其中有兩點有趣的現象。第一，在平均值附近的發生次數比描述隨機過程的常態分佈高了許多。第二，在遠離平均值的兩端的尾巴比一般還要厚，這正是所謂的『肥尾』或是『黑天鵝』。這個統計說明極端情形發生的頻率確實比預期的還要高。此外，我們也推測經濟的漲跌並非單純的隨機過程，而是可能摻雜了某種決定性機制的影響。混沌理論能和黑天鵝效應相容，這讓我們對混沌經濟學又更有了一點信心。
●大數據的指引
如同物理理論需要實驗的佐證，經濟理論也需要經濟數據來支持。透過混沌理論來解釋經濟問題目前尚不是主流，而大數據可能是他崛起的關鍵。在這個資訊爆炸的時代，不僅書本中、網路上充滿著資訊，人的一舉一動、各種經濟行為都流露出大量數據並被記錄下來。不同於在軟體業中認為數據及是金礦，在學術中數據更像是試金石。這些數據不僅幫助我們檢驗舊有理論的正確性，更將我們引導向更好的經濟理論。
--
本文整理自：105/6/4 由陳啟明教授在臺大思亮館國際會議廳所主講之「混沌的年代，混沌的經濟」演講內容。
