【探索15-7】有趣且不遵守比例原則的心臟與大腦

講師｜中研院物理所 陳志強研究員
撰文｜楊穎任

●神經系統是一個非線性的系統
一個滿足歐姆定律的電阻，其兩端的電位差與流過電阻的電流成比例。這樣的電阻屬於一個線性的系統，我給這個電阻幾倍的電流就會得到幾倍的電位差，他們是成比例的。但對於神經系統的作用單元－神經元來說，事情卻沒有這麼單純。神經元的細胞膜內外具有的一個電位差，稱為膜電位(membrane potential)。當我們給神經元一個流入內部的電流並量測膜電位如何隨時間改變時，我們會發現所得到的反應並不成比例而是非線性的。圖一中可以看到隨著給予的電流越來越大，膜電位的反應大小一開始與電流大小成比例。然而，當電流夠大時，膜電位卻有了一個快速的增減變化，稱為動作電位(action potential)。這個非線性的特性使得神經元可以像電腦裡的運算位元一樣可以傳遞穩健的資訊，並組成神經網路產生有用的功能或藉由彼此交互作用產生複雜有趣的運算。

 

在前面第二講與第四講的演講中，我們看到了簡單的非線性系統就可以產生十分複雜的動力學，甚至可以產成看似雜亂無章的混沌現象 [2]。而我們的心臟與大腦是由多個神經元(多個非線性系統)與其他輔助性的神經膠細胞所組成，神經元更可以組成複雜的網路。藉由神經元間的連結與交互作用，心臟與大腦中的神經網路可以具有什麼單一神經元所沒有的複雜特性呢？而什麼樣的神經網路可以使我們的心臟週期性的搏動而使大腦具有做複雜運算的能力呢？

●心臟中的可激發波
心臟的搏動靠得是各部位的心肌細胞有序的收縮。因為心肌細胞間可以直接靠細胞之間的間隙連結(gap junction)傳遞電流，心肌細胞可以產生動作電位 [3]、收縮並快速的刺激與它相鄰的心肌細胞。由於心肌細胞在產生動作電位後會有幾百微秒(約0.1秒)時間很難再被激發，訊息的傳遞變產生了方向性，並產生了可激發波。就好像在看棒球比賽時由人的起立坐下產生的波，每個人(心肌細胞)只需要看到隔壁鄰居站起來(產生動作電位)就被激發而跟著站起來，並在站起來後馬上坐下即可。

事實上這種可激發波可以具有複雜的結構。中研院物理所陳志強老師的實驗室可以讓老鼠的心臟在被取出體外後幾小時內仍具有跳動的能力。如圖二(A)所示，如果把這些心臟中的心肌細胞培養在培養基上並放在高倍數顯微鏡下觀察，就可以看到心肌細胞可以自己聚在一起並產生搏動。

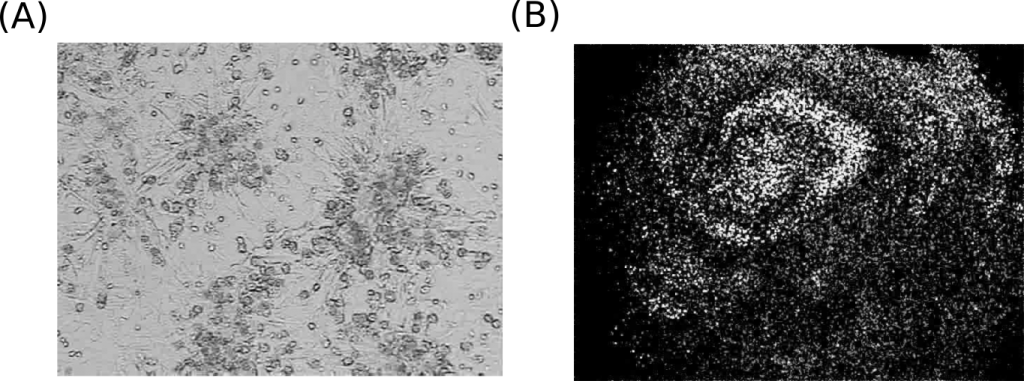
這時如果把鏡頭拉遠，在一個比較低倍數的攝影機下觀察，會發現系統會產生前述的可激發波且具有螺旋向外傳遞的特性，是謂螺旋波(見圖二(B))。螺旋波在其他非線性系統也可以被發現，譬如說一些特定化學反應(Belousov-Zhabotinsky reaction) [4] 或其他生物系統中 [5]。 如果這種螺旋波發生在心臟上時，此時的心率會比平常快上數倍，稱之為心室心律過速(ventricular tachycardia)，屬於心律不整的一種。如果不趕緊做適當的處理，更有可能造成螺旋波破碎成許多雜亂的小螺旋波(一種混沌的現象)。此時心臟將喪失血液幫浦的能力，稱之為心室纖維顫動(ventricular fibrillation) [6]。

心室心律過速或心室纖維顫動這種心律不整其實是一種非線性動力學的現象而非細胞的病變或感染。現今針對這種心律過速或心臟顫動的急救方法是使用自動體外心臟去顫器(AED)。它是利用給心臟一個極強的電流使每個心肌細胞近乎同時被激發並回復平靜，再配合CPR等急救技術使患者回復心跳。陳志強老師認為這種強行停止心肌細胞搏動的治療方法並不是最安全的方法。於是老師的實驗室也嘗試利用如 回饋控制等方法控制心律不整的問題。我們也期望在對於心臟中的螺旋波有更深入的了解後，我們可以研究出針對心律不整有效的解決方法。

●腦神經網路中的自發反應與自組織臨界性
相較於心臟，大腦是一個更為複雜的器官。科學家估計人類大腦有大約 個神經元，足足比世界人口(約 人)多了約10倍。這些神經元更可以藉突觸(synapse)相互連結與交互作用，大腦中的突觸更多達 個 [7]。 這些連結甚至可以隨著大腦的動態改變其強度。想要了解這樣一個龐大的動態神經網路可以說是近乎不可能。然而科學家相信不同的網路與其動力學性質對應到不同的大腦功能或運算，想要了解大腦勢必要了解神經網路根據什麼樣的規則可以產生相應的運算與功能。一個簡化問題的辦法是先研究較小型的神經網路，例如生長於培養基上的小型腦神經網路，陳老師的實驗室利用具有多個電極的探針陣列紀錄此腦神經網路的活動並嘗試了解這樣的簡化系統。

實驗發現這樣的小型腦神經網路可以自發產生複雜而有趣的反應。如圖三所示，電極可以偵測到一些同步的自發反應，而這些反應在時空上似乎具有自相似性。

如果我們統計在一次自發性反應裡神經網路有多少動作電位產生(如圖三(B))，並定義此數量為一次自發反應的大小 。實驗更發現這些自發反應的大小與其出現的機率具有冪次(power law)的關係： ～ (如圖三(C))。這種自相似性與冪次關係在雪崩或地震的系統也常常被發現。由於在物理中，自相似性與冪次關係是系統在相變化的時候特有的性質，這種在動力學系統中發現的現象被稱為自組織臨界性(self-organized criticality) [9]。 相似的現象不僅在培養的腦神經網路上發現，老鼠皮層切片上也有發現這樣的自組織臨界性 [10]。 值得注意的是，這種現象並不是單一神經元所具有的，而是從眾多神經元間彼此的交互作用出現的湧現性質(emergent property)。

然而大腦是否具有自組織臨界性其實仍是一個有爭議的問題。相較於追求穩定與有序的心臟來說，我們可以預期腦神經網路應具有更為複雜甚至接近於看似無序(混沌)的動力學。畢竟一個腦神經網路如果太過於同步或是有序，其可以傳遞與處理的資訊量勢必受到限制。研究者們進一步指出一個具有自組織臨界性的神經網路可以具有最大的可反應刺激範圍、最大的資訊保真度與最大的資訊儲存量 [11] 。至今，科學家仍致力於研究哪些腦神經網路會具有或是需要具有此種自組織臨界性。可以被確定的是，我們正在深入了解大腦的路途上前進著。

●結語
心臟與大腦是由許多非線性的單元－神經元與其他輔助型細胞所組成。藉由這些神經元的交互作用，我們的心臟與大腦可以具有其所需的功能。心肌細胞間的交互作用使他們可以產生可激發波。這些可激發波在心臟的正常運作上扮演重要的功用。藉由研究複雜的可激發波，科學家有望對於異常可激發波造成的心律不整提出根本性的治療之道。大腦中的神經網路又比心臟更為複雜。藉由研究較為簡單的系統例如培養基上的腦神經網路，科學家可以對於腦神經網路的性質有更深入的了解。研究這類神經系統不僅僅可以對於醫學上有直接的貢獻，更可能藉由了解大腦的運算原則對於電腦的設計產生革命性的影響。

參考資料：
[1] Sulayman D. Dib-Hajj et. al., “NaV1.9: a sodium channel linked to human brain.” Nature Review Neuroscience (2015).
[2] 例如這兩期提到的logistic map以及lorenz system。皆可在英文的Wikipedia找到完整的介紹。
[3] 心肌細胞的動作電位與圖一所顯示的略有不同。動作電位的型態與時間尺度皆有所差別。可以詳見Wikipedia對於Cardiac action potential的介紹。
[4] 請見Wikipedia：Spiral wave提到幾個常見的螺旋波在生物系統的例子。
[5] 請見Scholarpedia：Belousov-Zhabotinsky reaction對於此反應的英文介紹。
[6] 請見Scholarpedia：Cardiac arrhythmia對於心律不整的英文介紹。
[7] 請見Wikipedia：Orders of magnitude (numbers)中的估計與其來源。
[8] S. Pajevic and D. Plenz, “Efficient Network Reconstruction from Dynamical Cascades Identifies Small-World Topology of Neuronal Avalanches” PLoS computational biology (2009).
[9] 請見Wikipedia：Self-organized criticality對於自組織臨界性的英文介紹。
[10] C. Haldeman and J. M. Beggs, “Critical Branching Captures Acitivity in Living Neural Networks and Maximizes the Number of Metastable States” Phys. Rev. Lett. (2005).
[11] W.L. Shew and D. Plenz, “The Functional Benefits of Criticality in the Cortex” The Neuroscientist (2013).

--
本文整理自：105/5/28 由陳志強研究員在臺大思亮館國際會議廳所主講之「心臟和大腦中的有序和混沌」演講內容。