【探索15-3】勞倫茲，蝴蝶，以及他們共同掀起的混沌風暴

講師｜臺大物理系 陳義裕教授
撰文｜蕭維翰

本期講座由龐加萊 (Henri Poincare) 在 19 世紀開創性的工作起始，說明了混沌現象的發現與其相關的歷史脈絡。然而，前者並不常是普羅大眾對於混沌的啓蒙，更廣為人知的混沌相關現象應當是所謂的「蝴蝶效應」(butterfly effect)。該術語的歷史起源可追溯於 1972 年勞倫茲 (E. Lorenz) 於美國科學促進會 (American Association for the Advancement of Science) 的演講題目「若一隻蝴蝶在巴西振翅，是否會造成在德州的龍捲風呢？」，泛指勞倫茲方程式以及其他混沌系統對於初始條件的敏感所衍生的現象。因此，本講的主題即著眼於該方程組與其解組成的圖像，在定性的層次上了解所謂的蝴蝶效應，以及粗略地探討其他遵守類似方程式的系統展現的物理現象與應用。

電磁學與相對論教科書中並不乏所謂的「勞倫茲先生」，分別是 L. Lorenz 與 H. Lorentz。知名電動力學教科書作者 J. D. Jackson 曾為文說明電動力學中所謂勞倫茲規範 (Lorenz gauge) 是以前者為名，但許多教科書常誤植成後者，乃至於今日的許多學者亦常混淆。而混沌現象的勞倫茲則又另有其人，是生於 20 世紀的 E. Lorenz ，主攻氣象學與應用數學。

位於風災的熱區，臺灣對於氣象科學的實用性理應易有深刻的體認。這些氣候的變化可以視為空氣、水等流體的交互作用，也因此可以透過流體力學來研究一些簡單的模型，在勞倫茲的文章中，他將原 Saltzman  的流體對流模型簡化成三個常微分方程式，亦即陳教授在演講中所展示的勞倫茲方程組。

●勞倫茲方程組

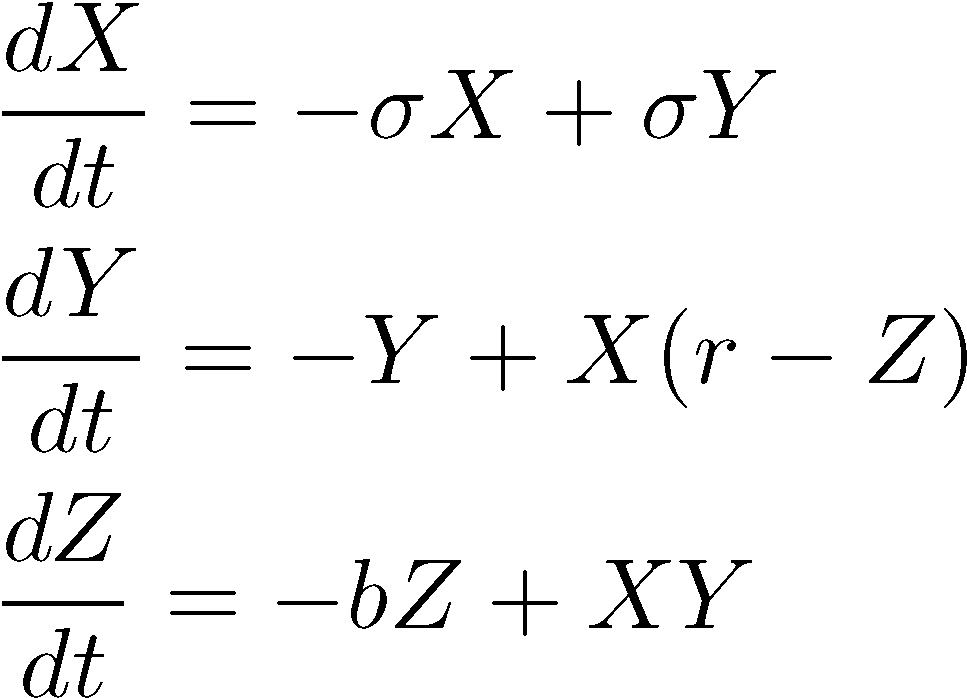
在這邊我們再一次說明不同變量代表的意義：X 正比於對流的強度、Y 代表上升與下降流體間的溫度差、Z 的意義比較不是那麼白話，它可以視為對於一種給定溫度分佈的偏離程度。因而第一個方程式說明流體的強度如何被自身的黏滯力與熱對流影響；第二與第三個方程式則說明 Y 與 Z 這兩種溫度如何因彼此的熱導與流體攜帶熱量的關係而變化。

勞倫茲證明了這組方程式的解會集中在相空間（此處可理解成 (X, Y, Z) 組成的空間）內某個區域，並且找到了幾組靜態解，如 X = Y = Z = 0。但這樣的解顯然不是我們需要的，對於非週期性的解，勞倫茲指出他們都不穩定。也就是說，我們選取相差不多的初始狀態，經歷一段時間後，結果也會大相徑庭。透過這點可以推論，即使勞倫茲方程式可以用來模擬天氣的演化，我們也需要整個世界的完整資訊（無限精準的初始位置、速度等），才有實際的預測能力，這也是為什麼一隻蝴蝶搧動翅膀，都可能對未來造成巨大的影響。

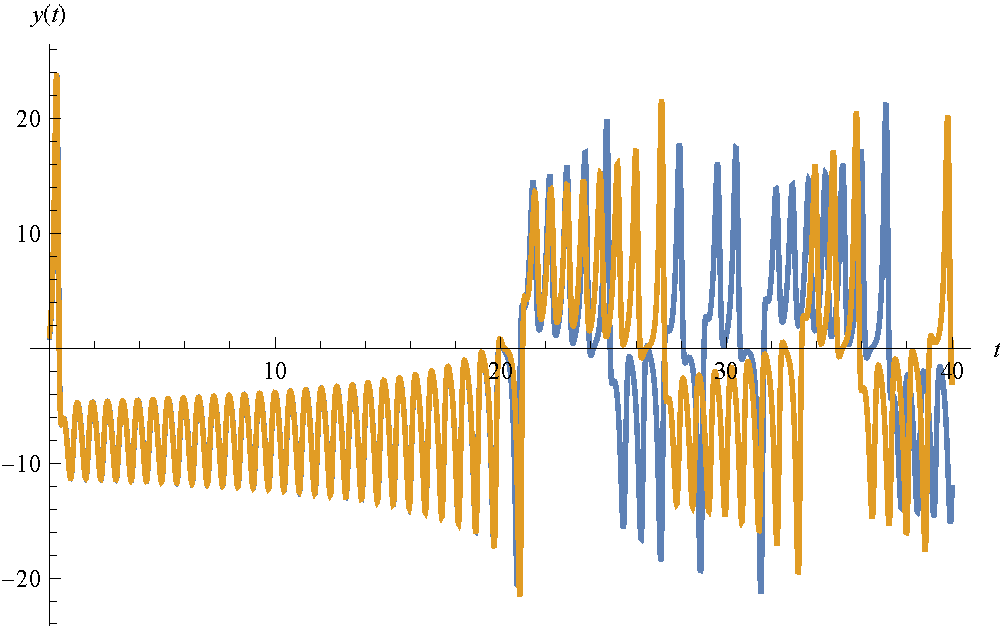
現代許多電腦軟體都有能力繪製勞倫茲方程的解，採用跟原文一樣的參數，並考慮 X(0) = Z(0)=1，Y(0) = 1 或 1.1 兩組初始條件，我繪製了以下三圖，圖 1 是 Y 對於時間  t 作圖，我們發現當 t 在 0 和 20 之間時，兩組 Y 並沒有顯著的差別，然後之後它們之間的關係便幾乎是無跡可尋了，根據這個線索，我繪製了圖 2，當 t 在 20 跟 25 之間兩組 (X, Y, Z) 的演化情況，很明顯在 t = 25 時，它們在相空間中並不靠近，也就是若我們的初始條件與大自然的真實狀況有 10 % 的誤差，在 20 個時間單位後，人類的解就失去了預測的力量。圖 3 則是考慮但一組 (X, Y, Z) 在空間中的軌跡，一如前言，這些解會被侷限在相空間中的區域，而這個圖樣即是有名的勞倫茲吸子（Lorenz attractor）。在吸子旁邊的軌跡，儘管混亂無序，卻總是會往這個吸子靠近。

 

 

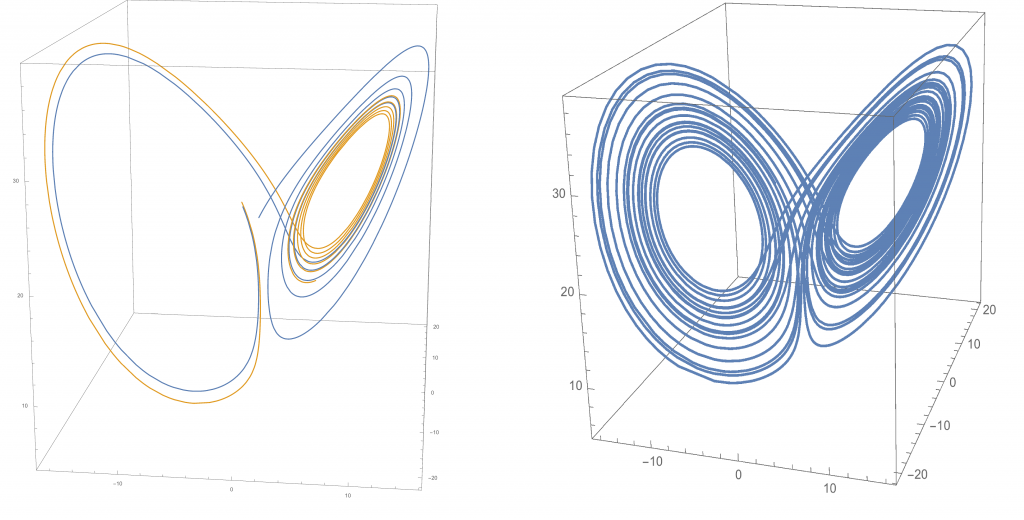
儘管沿著時間的軌跡看似雜亂無章，但這個系統在空間中的映射卻有規律而有趣的性質。在圖 4 中我考慮某段時間內的 (X, Y, Z) 軌跡與空間中 X-Y 的某一個截面，在截面上有些點被軌跡穿過，那問題是：某一個截點沿著軌跡運動下一次再通過截面時，會落在哪一個地方呢？這樣點與點間的關聯形成了一個從平面到平面的一個映射，令人驚豔的是，對於某些集合，經過一次的映射會分成 2 個小集合，從而分成 4 個、8個 ......，最終形成一個所謂 Cantor 集的集合，一個混沌的系統竟蘊含了碎形的概念。

前兩段約略地說明了勞倫茲方程組，那為什麼要特地寫出方程組並研究呢？定量科學的一部份工作在於建構模型嘗試說明自然現象。然而，困難到無跡可尋或者太簡單而無法推論任何現象的模型實用意義都不大。好的模型往往講求合理的可解性，與預測基本物理現象的能力。便如大部份的讀者在高中都學過簡諧運動 (simple harmonic motion) 意義就在在線性系統中它是簡單可解的，並且抓住了震盪這種常見現象的神髓，以至於高等物理學其他分支中我們也都從簡諧運動的類比開始探討。

同理，對於科學從業人員而言，勞倫茲方程並不是一個太面目可憎的問題（舉例而言，相較於龐加萊的三體問題，顯然這個方程式單純的多。）其解卻已展示了混沌這種深刻的現象，因此有些時候我們可以將它當成混沌系統的簡諧運動。像是預測地磁翻轉的玩具模型，透過一些近似，描述該系統的方程式與勞倫茲方程並無二致，因而人們便可以透過現有對勞倫茲系統的了解對地磁反轉的問題有一些理解。

●接著我們要問，人類能應用混沌嗎？
混沌的表象是很亂的，但人類生活也不乏需要混亂的場合，如在電腦科學的運用中我們常需要產生隨機亂數，倘若背後的機制有一定的脈絡，那便不是隨機了。這種透過混沌產生看似無序的映射甚至被應用到了音樂的編曲上，1995 年左右 MIT 的博士生 Diana Dabby 透過起始音調將樂曲分段，並配合勞倫茲方程的解序列編排。因為此系統對初始條件極為敏感，稍微不同的起始條件變成產生出相差極大的編序，然而吸子此處扮演了原曲的角色，因此不論怎麼演化，還是會趨向原曲的風格。Diana 將這樣的映射技巧應用到了巴哈的音樂中，編纂了一系列「無一音符非自巴哈，卻又無一曲譜自巴哈」的鋼琴作品。

半個世紀以來，從勞倫茲當時原文對氣象預測無望的悲觀結論；到今日，人們已可藉由混沌系統加密傳訊乃至編曲怡情，我們的確不清楚牛頓是否認知到了混沌的存在，遑論暗藏在混沌之內的可能性，但或許已經逐漸體會這樣的可能性，還遠遠超乎想像。

參考資料：
[1] E. Lorenz, Journal of the Atmospheric Science 20 (2): 130-141 (1963).
[2] D. Dabby, Chaos 6 (2): 95 (1996)

--
本文整理自：105/4/16 由陳義裕教授在臺大思亮館國際會議廳所主講之「勞倫茲，蝴蝶，以及他們共同掀起的混沌風暴」演講內容。