人臉辨識的困難與突破(下)
機器可有人類的視覺能力嗎?以單張影像,機器想要和人類的精確視覺相提並論或許還早。但機器的快速與大量能力,已經遠遠超越人類了。在茫茫的網路相片海中,機器可以幫你找到您的親人,只要您給它適當的特徵!
撰文/楊家輝(國立成功大學電腦通信工程研究所特聘教授)、黃世明、吳思樺
轉載自《科學月刊》2013年2月第518期
(續前文)
●人臉辨識演算法

對於人臉辨識的問題,通常我們將二維(q x p)影像影像矩陣轉為一維(qp ×1)向量。如果我們收集多個因燈光、時間、表情、穿戴不同的人臉向量,該向量均有其分佈向量空間(vector space),不同人佔有不同的向量空間。人臉辨識的問題就變成,如何於向量空間中尋求一個判斷範圍曲面,將其分佈向量空間進行分類。
如圖三所示,若我們有A、B、C三人,這三者之向量分別為(xa,1, xa,2,…, xa,N), (xb,1, xb,2,..., xb,n), 及(xc,1, xc,2,…, xc,N),其三者有其向量空間分佈。最簡單的辨識方式,我們可求每個人之向量空間之中心分別為:
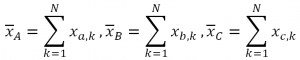
當我們有一未知人臉之向量xtest , 其辨識的方法可求向量xtest與三個向量空間之中心的歐式距離,
![]()
若dA最小,我們就可將此未知人臉辨識為A。
為了達到更精確的人臉辨識,常用的演算法包括:主成份分析法、線性鑑別分析法、線性迴歸分類法。我們先介紹該方法之原理,再接著介紹我們提出的核線性迴歸分類法,以及實驗比較結果。
主成份分析法(PCA)
首先是由Karl Pearson 在1901 年所提出,而將PCA 應用於人臉辨識上則是始於Matthew Truk 與 Alex Pentland 在1991 年所提出的(特徵人臉)辨識系統。主成份分析法的主要目的為了降低影像的維度以達到降低運算量的目的,在訓練階段藉由尋找出重要的特徵向量來描述訓練集合中的人臉影像。主成份分析法意即透過y=WTx 的矩陣轉換,將原始維度為n的影像投影降至新的維度為m的空間中(m<n),並找到最佳的n×m 投影矩陣W。以類別總數為兩類來說明,如圖四所示,圖中有兩群資料(+與×),主成份分析法會以最能代表所有資料的主要成份向量來表示原有資料x,即透過由主要成份向量所組成的投影矩陣W沿著虛線,得到降維後的投影資料y。可以想像是原本二維資料投影變成一維資料,而投影後的資料分佈如圖四右下角的直線所示。主要成份向量可以透過計算原有資料共變數矩陣的特徵向量(eigenvector)所得,並選擇前m 大的特徵向量為主要成份向量並列成投影矩陣,其中m為欲降至的維度。透過此投影矩陣得到降維後的資料。在辨識階段,新的測試影像xtest進來,也將其透過W得到降維後的測試影像ytest,利用如圖三之簡易影像辨識法,並計算ytest到每個降維後的資料間的歐式距離,而與ytest距離最短的資料所屬的類別即為最後辨識結果。
線性鑑別分析法(LDA)
目的是將同一類別的資料經過投影後距離越近越好,而不同類別間的資料投影後的距離越遠越好。以類別總數為兩類來說明,如圖四所示,圖中有兩群資料(+與×),線性鑑別分析法會以最能分離不同類別資料的成份來進行降維。可以想像是原本二維資料變成一維資料,如圖四左下角的線上資料分佈情形。
由以上介紹,我們可以發現因為線性鑑別分析法有考慮不同類別的資料分佈情形,所以,如圖四所示,線性鑑別分析法的重疊區較小,反之,主成份分析法的重疊區較大。因此,可以預期線性鑑別分析法的辨識率會比較高。

線性迴歸分類法(LRC)
線性迴歸應用於人臉辨識是始於Roberto Togneri 與Mohammed Bennamoun在2010 年所提出。在訓練階段中,目的是要在原線性空間中找到每一類的投影矩陣Hi,以類別總數為兩類來說明,如圖五所示,兩類各自有不同的投影矩陣,分別為H1與H2。而當一測試影像ytest進來時,透過投影矩陣求得ytest在這兩類別空間中的投影點與,並計算ytest到各投影點的歐式距離,與ytest距離最短的投影點所屬的類別即為辨識結果。

核線性迴歸分類法(KLRC)
在介紹核線性迴歸分類法( 簡稱KLRC) 方法之前,以下先介紹核轉換法(Kernel method) 與核函數(Kernel function)。核轉換法已應用在許多圖形分析與辨識上,最主要的目的是要透過轉換函數φ使資料以非線性的方式映射至較高維度空間上的空間上,使得資料空間經過非線性之扭曲,以增加核轉換後之資料較易被分類。但是在這較高的維度中很難運算,所以我們可以將核心函數以代換式子表示,則可以避免直接計算高維度資料,此方法稱為核秘訣(kernel trick)。因此,原始的線性演算法也經核秘訣之轉換函數φ變成非線性演算法。
所以,利用核轉換法原將線性迴歸分類法(LRC)轉換成非線性之核線性迴歸分類法(KLRC)。如圖六所示,先將原資料經由φ轉換到另一非線性空間。實際上,圖六中之平面於原來空間實為一經φ轉換扭曲之曲面。在訓練階段中,在非線性空間中找到每一類的投影矩陣,以類別總數為兩類來說明,如圖六所示,兩類各自有不同的投影矩陣。而當一測試影像ytest進來時,透過投影矩陣求得ytest在這兩類別空間中的投影點與,並計算ytest到各投影點的歐式距離,與ytest距離最短的投影點所屬的類別即為辨識結果。

●研究案例:低解析度且燈光變化之人臉辨識
監視器所拍攝到的人臉影像解析度都很小。使用如此少的人臉影像資訊要得到準確的人臉辨識率是非常困難的,因為這些低解析度影像中缺少人臉辨識所需的重要資訊。因此,如何在低解析度下進行人臉辨識是有趣的問題。不僅如此,在日常生活中,燈光或亮度的影響是必然發生的問題。所以,如何在很小的人臉影像且燈光變化下獲得準確辨識是非常重要。以下實驗將顯示以上介紹過的方法在很小的人臉影像且燈光變化下的辨識率。
實驗規則
本實驗使用Yale B人臉資料庫,此資料庫中包含十個人,每人有九種姿勢,每個姿勢有六十四種燈光變化。實驗中只考慮資料庫內的正臉搭配上六十四種燈光變化,並將每張影像裁減並調整大小為8×8,如圖七所示。資料庫依照不同方向角度的燈光來源分為五個子集合,總共六百四十張影像,每個子集合分別為:70張(每人7張)、120張(每人12張)、120張(每人12張)、140張(每人14張)、190張(每人19張)。實驗設計為使用第一個子集合為訓練資料,而第二到第五個子集合分別為測試資料。

實驗結果
如圖八所示,統計資料顯示各種方法的人臉辨識率(%)比較結果,以上介紹的幾種方法中,以PCA 的表現最差,因為PCA 無法克服燈光變化的問題,更何況在低解析度且燈光變化的問題。另外,LDA 與LRC,在子集合二及子集合三的人臉辨識表現尚不錯,但是在子集合四及子集合五下就無法得到滿意的表現了,尤其是在子集合五的情況下。最後,我們提出的KLRC 的表現比其他方法好。在子集合二及子集合三的人臉辨識率皆達到100%,在子集合四的表現有超過90%,尤其是在子集合五的情況下,人臉辨識率有明顯提高。本研究已被2012 年國際電子電機工程學會(IEEE)之聲音語言暨信號處理研討會(International Conference on Acoustics, Speech, and Signal Processing 2012)接受並且出席口頭發表。

●結論
本文介紹機器學習的歷史以及應用範圍,並且探討人臉辨識的應用、困難、基本原理,及其最新方法。人臉辨識是機器學習於視覺領域中的一種應用。簡單而言,人臉辨識乃利用向量空間的空間關係尋找最佳的分割曲面。最近,已經有愈來愈多人臉辨識相關應用產品相繼推出,這顯示人臉辨識在日常生活中的重要性。本文希望增加一般民眾對人臉辨識的認識,並對未來人臉辨識的發展之認識有所助益。(完)
參考資料
- Huang, S., & Yang, J. (2012). Kernel linear regression for low resolution face recognition under variable illumination. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 1945-1948.
- Naseem, I., Togneri, R., & Bennamoun, M. (2010). Linear Regression for Face Recognition. IEEE Transactions On Pattern Analysis And Machine Intelligence, 32(11), 2106-2112.
- Yale Face Database. Cvc.cs.yale.edu. (1997).
- Zhao, W., Chellappa, R., Phillips, P., & Rosenfeld, A. (2003). Face recognition. ACM Computing Surveys, 35(4), 399-458.
(本文由教育部補助「AI報報─AI科普推廣計畫」取得網路轉載授權)
