【探索22-8】可算?不可算?這是個電腦問題
我們在日常生活中享受著各種智慧產品所帶來的方便,由於電腦強大運算能力帶來的低延遲,很容易就讓人忘記這些方便其實來自於電腦在背後進行的巨量運算,也容易忽略電腦能解決的問題其實有其限制。董世平教授將從簡單的數學問題出發,介紹電腦的可算性、可行性,探討當今電腦科學界數一數二重要的問題,帶我們認識現在計算科學的樣貌。
 講者|中原大學應用數學系教授 董世平
講者|中原大學應用數學系教授 董世平
彙整撰文|蘇建翰
●簡單問題不簡單
如何找出「 x2-2x-15=0」的整數解,在課本裡就能在一元二次方程式章節看過類似的題目,對於某些熟悉的人來說或許只要透過心算即可解決,然而這道看似初階的題目真的有那麼簡單嗎?我們都知道簡單與否是因人而異的,那麼對於電腦來說,要解這道題目也是簡單的嗎?
歸功於電腦強大的計算能力,有些較單純的數學問題透過wolfram alpha等運算平台只消片刻就能獲得答案。在這看似不費吹灰之力的過程背後,由於無法和人類一樣進行抽象思考以及紙筆運算,電腦其實仰賴許多演算法來應對不同的數學問題。無論是採取哪種方法,選擇每一個方法的背後都有其數學的理由,譬如要解開前述一元二次方程式的題目,可以透過暴力法進行搜索,也可以透過因數法測試因數分解後得到可能的候選值再進行判斷,又或者可以利用因式法直接進行因式分解得到答案,這些不同的方法背後都有其數學定理支撐。
●希爾伯特第十問題的答案
讓我們更進階一點,思考如何找出「x2-631y2-1=0」的所有整數解,或許有人一眼就能看出來,(x,y)=( ±1,0)即為兩組解,不過下一組整數解的數量級已經暴漲至x=48,961,575,312,998,650,035,560、y=1,949,129,537,575,151,036,427。由此可以看出,即使只是一個簡單係數的二元二次方程式,解答很容易就落在多數人計算範圍之外,面對這類問題,我們可以寄希望於電腦嗎?這個問題的答案令人驚訝,至今為止「沒有方法」可解所有的二元整數方程式。
十九世紀末,德國數學家希爾伯特(David Hilbert, 1862-1943)提出了二十三道數學問題,期望能在接下來的二十世紀中獲得回應。其中,第十道問題即是詢問「是否能找到一個方法,可以在有限的步驟內,決定任一個整數方程式是否有整數解?」,這個問題在數學家的努力下,得到的答案是「沒有方法」(MRDP定理),這個答案很有趣,說不定也出於當年希爾伯特的意料之外,而這個「沒有方法」究竟是什麼意思?這個方法究竟存不存在?現在不知道難道以後也不知道嗎?
任何電腦能夠執行的工作都是杜林機可算的問題,根據邱池—杜林論題(Church—Turing thesis),任何可計算的問題,都是杜林機可算的,相對的那些杜林機不可算的問題,就是被認為「沒有方法」可以解決的問題。所謂的「沒有方法」並不等同「方法存在只是還沒找到」,更精確一點的說,其實就是「這個方法不存在」,如果從計算的角度來說,「沒有方法」指得就是無論未來電腦如何發展,給予不受限制的時間與資源仍無法透過電腦解決。這一類和方程式整數解一樣「沒有方法」、電腦無法解決的問題,我們就稱作是「不可算問題」。
●P = NP?
前述針對可計算性的討論,通常是不限時間與空間的,不過現實中所會碰到的問題常常會需要在受限的時間以及記憶體空間下解決,在此種狀況下,需要考慮計算繁度,換句話說,我們除了思考有沒有方法,也想探究有沒有足夠好的方法。要比較不同方法的好壞,作為衡量基準的,通常是當問題變得非常複雜時,解決問題所需要花費的時間。
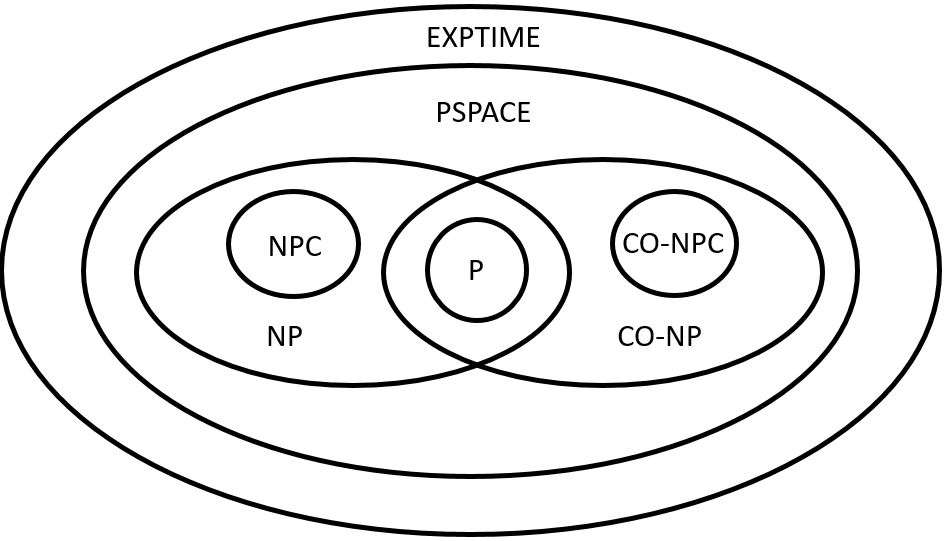
杜林機可以被分成確定型(deterministic)和不確定型(non-deterministic)兩類,前者即是一般通稱的杜林機,在運作中由當前的值和狀態決定下一步,因此下一步只有一種可能,這也是目前電腦普遍運作的方式;後者則是在選擇下一步時,同時有多種可能的路徑可以選擇。要注意的是,這兩種杜林機可以解決的問題是一樣多的,差別在於兩者之間所需要的時間不一樣。如果一個問題,可以被確定型杜林機在多項式時間被解決的話,這一類問題我們就稱為「可行(feasible)問題」,一般以P來表示;相對的,不在P中的這類問題就是「非可行(Infeasible)問題」,可以被非確定型杜林機在多項式時間被解決的話,這一類問題我們就稱為NP問題,另外,NP否定問題稱為CO-NP問題。在NP問題中,最難的一類問題被稱為NP完備(NP-Complete, NPC),其否定問題則稱作CO-NPC。
當今對計算繁度的分類有多種猜測,而其中被認為是電腦科學及數學最重要的問題之一的,即是P是否等同於NP (P=NP?),被列入克雷數學研究所(Clay Mathematics Institute,CMI)懸賞一百萬美金的七道千禧年大獎難題之中。P是否等於NP和數位時代的生活息息相關,現在常用的RSA加密演算法其核心是由質數乘積來加密,質數乘積一般被認為是一個陷阱函數,也就是計算容易但逆轉計算相當困難的函數,破解密碼需要質因數分解這是個NP問題,一旦我們可以證明NP等於P,就可以將NP轉換成P問題來處理,破解密碼將會成為可行問題,對現行的資訊安全將會造成極大的威脅。
在當前的電腦架構下,大部分電腦科學家的看法為 ,因此,若一個問題已經被證明為NP完備,其求最佳解則被認為非可行,遇到這一類非可行問題,隨著問題的複雜度增加,即使目前電腦運算速度成長日新月異,計算能力提升所帶來的解題效率也無法顯著提升。
●量子計算增添計算科學的樣貌
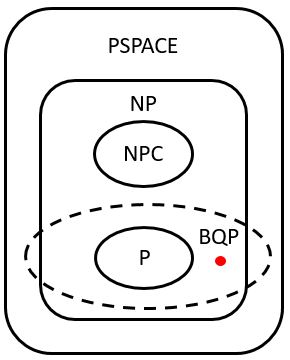
量子計算近年來成為熱門的領域,在確定型杜林機以外開創一條不同的計算形式。雖然量子計算的可算性與確定型杜林機相同,不過量子計算的可行性與確定型杜林機可能有所不同,所以也多了一種衡量計算繁度的指標,稱為BQP(Bounded-error Quantum Polynomial Time)。譬如,對於傳統杜林機來說是NP的因數分解問題,就有多項式時間的BQP量子演算法,因此有人猜測因數分解可以成為可行問題,如果這個猜測在未來被證實了,就如上述,傳統上使用RSA加密的資訊就需要另尋他路來保護資料安全。
電腦的運算能力進入二十一世紀以來顯著成長,受惠於此許多研究、工程領域產生不少應用,讓我們的生活更便利。在應用端,一如前面提過的尋找整數解、質因數分解等問題,回到最源頭的數論、計算科學仍有許多有趣的、重要的問題等待探索,這些問題能否被解決、有沒有答案,將會決定下個世代計算的面貌。
--
本文整理自:108/12/7由董世平老師在臺大思亮館國際會議廳所主講之「可算?不可算?這是個電腦問題」演講內容。
