淺度量子電路 – 現階段真正的量子優勢
■量子優勢(Quantum Supremacy) 是一個假說,指的是量子電腦擁有任何古典電腦都無法匹敵的計算能力。各大研究機構、政府和公司都正積極發展量子電腦,其原因非常明顯:誰能掌握最強的計算能力,誰就能掌握包含人工智慧、情報和安全通訊等科技的主宰權。但是在現階段,量子電腦還處於嬰兒時期,而且量子優勢是否真實存在還是一個未知數。本文介紹現階段量子電腦的合理應用,以及IBM 科學家證明量子電腦在某個常見的問題具有絕對優勢。
撰文|陳奕廷
●近期的量子電腦架構:淺度量子電路
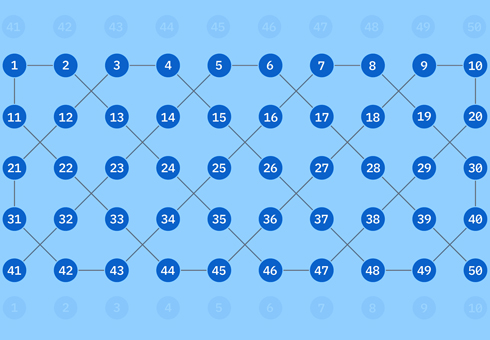
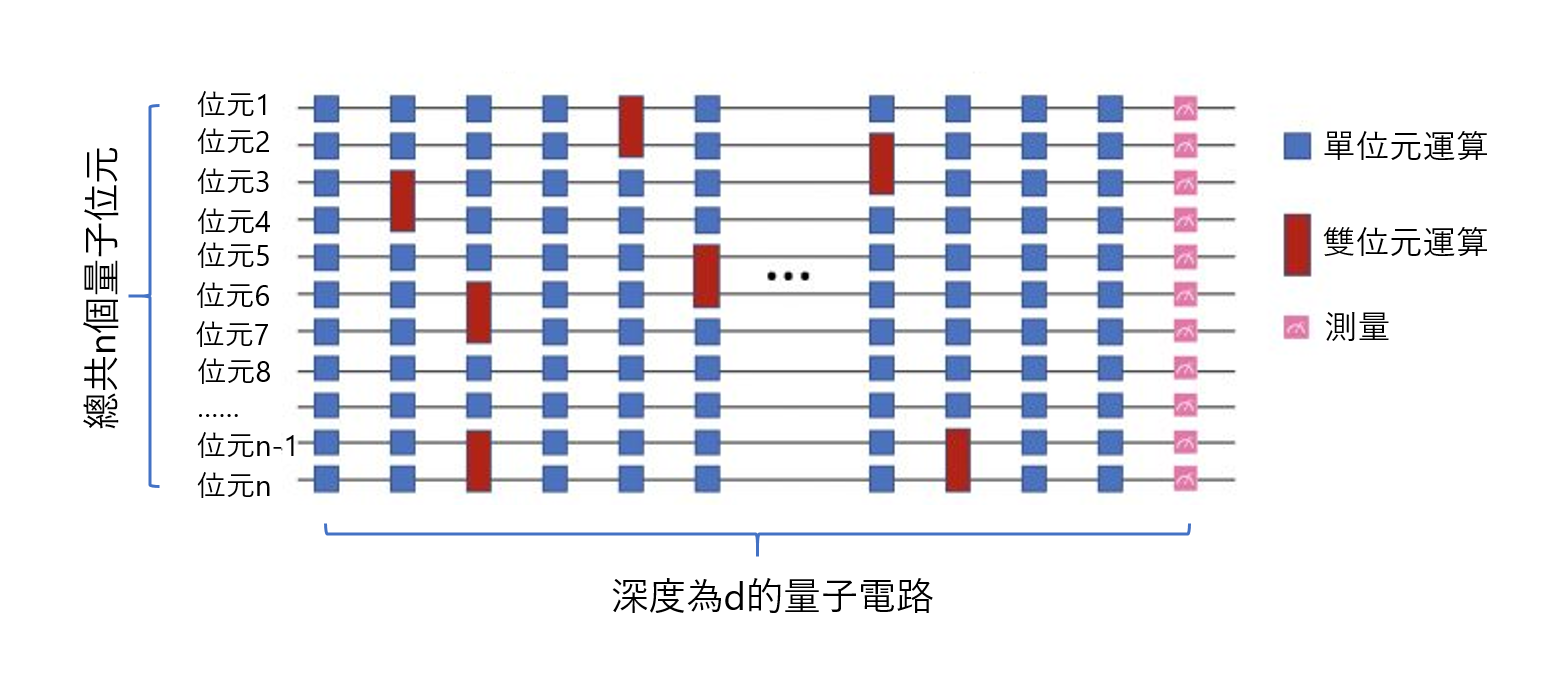
在古典電腦中,只要時間夠多(還有電費不太貴),我們能執行任意長的運算。但在量子電腦中,由於目前量子位元的錯誤率高,量子電路只能進行有限的運算次數。也就是說,如果量子位元數目是n,量子電路的深度是d[註1],c=n*d這個數字是固定的。當量子位元數目n越大,古典電腦越難與其抗衡,所以n越大的量子電路是比較有用的。換句話說,在現階段d越小的量子電路是比較有實用價值的。科學家把這類d很小的量子電路稱作「淺度量子電路(Shallow Quantum Circuit)」(如圖1)。這個量子電路有一個特性:在每一層運算中,一個量子位元只進行一次運算,所以運算之間沒有先後順序。因此,同一層內的運算可以完全平行化,在一次的運算時間內,就能完成所有同層內的運算。圖1之中深度d的量子電路,只需要d次運算時間就能完成。由於運算時間跟量子位元數目n無關,這種電路的計算效率被稱作「常數時間」,是最有效率的運算複雜度。
●如何正確衡量「量子優勢」
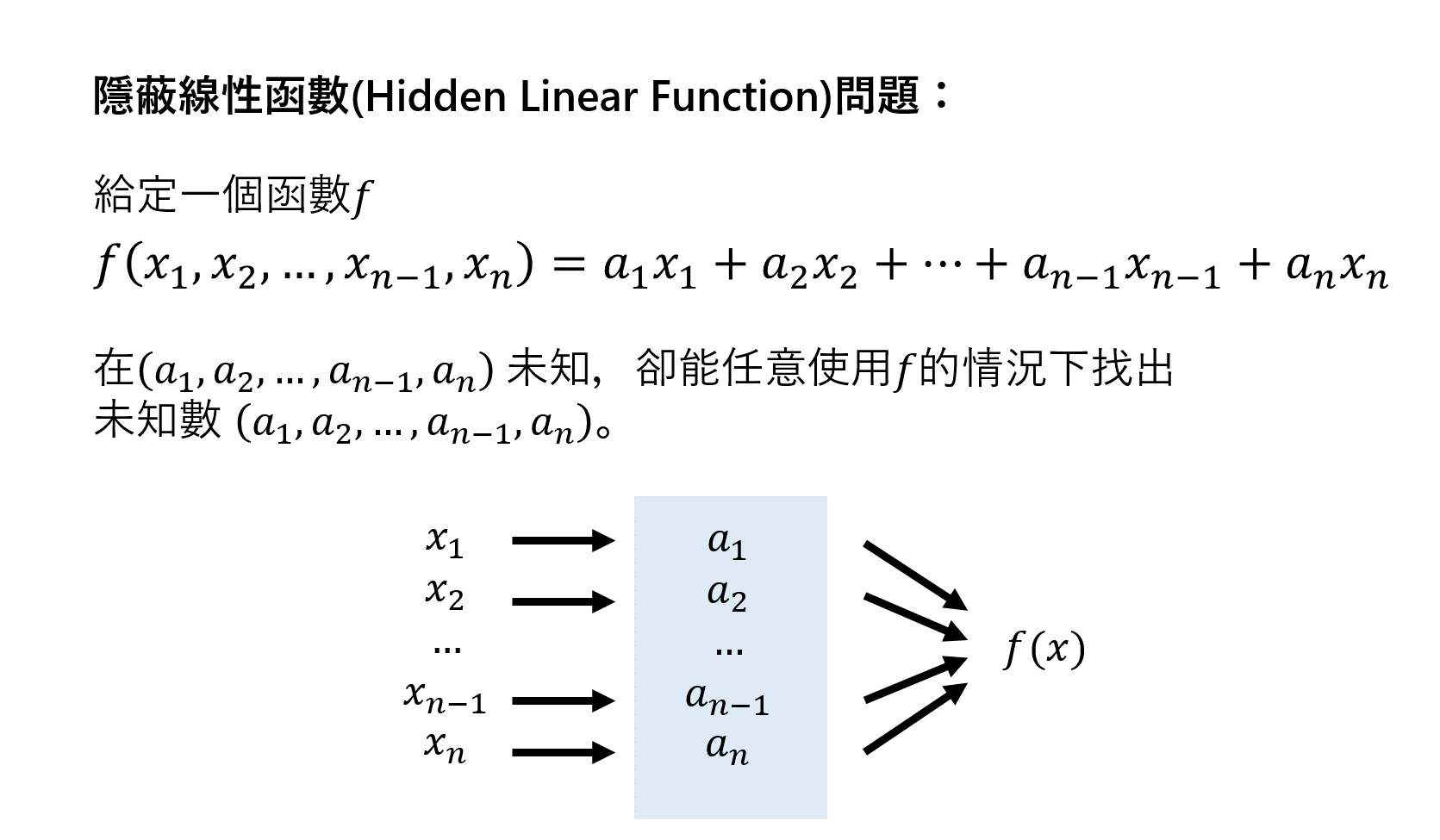
古典計算複雜度是用來衡量一個演算法效率的標準,通常以加減乘除的運算次數或時間來決定。舉例來說,如果一個演算法在n個節點間找出最短路徑需要進行n平方次四則運算,我們會說它的計算複雜度為n平方。但是量子電腦的運作原理並不是由四則運算所構成的,所以效率難以用古典計算複雜度來衡量。因此,科學家用另外一套標準來衡量量子電腦的效率。以圖2中的問題為例,科學家用解決問題時呼叫函數f(x)的次數來衡量效率。古典電腦需要呼叫f(x)函數n次才有足夠的資訊解決問題,而量子電腦只需要呼叫1次[註2]。根據這個呼叫次數的差異,許多科學家認為量子電腦比古典電腦還要優越。
這種比較方式就像是比較海豚和猴子的爬樹能力,對古典電腦太不公平。於是IBM科學家近日提出更公平的標準來衡量古典和量子的計算能力[參]。儘管量子電腦不使用四則運算,但還是有類似邏輯閘的結構。新的衡量標準 古典計算複雜度:比較使用邏輯閘的次數和時間。如果能在這個標準上打敗古典電腦,量子電腦才算是真真正正的具有優勢。
●以「隱蔽線性函數問題(HLF)」為例
在新的標準下,要證明量子電腦在所有問題都比古典電腦優越是一個困難的問題。所以科學家目前只侷限於HLF問題。如圖2,HLF看起來複雜,但它常常在決策和搜尋問題中出現,是一個常見的問題。使用新的標準在這個問題中,IBM科學家證明量子電腦仍具有絕對優勢。詳細證明不在此描述,有興趣的讀者可以閱讀參考資料。簡單來說,HLF可以用上述的淺度量子電路來解決,所以計算複雜度是常數時間,而古典電腦的複雜度是log(n)。換句話說,隨著問題的大小增加(n增加),古典電腦需要的運算時間呈現對數增長(log(n)),但是量子電腦需要的運算時間卻不變。
●「非局域性」是量子優勢的關鍵
IBM科學家更進一步地指出量子優勢背後的關鍵之一是「非局域性」,其對應的物理現象叫做量子糾纏。量子糾纏讓一個量子位元的資訊不只在自己身上,也分散儲存在其他位元中。這種非局域性的資訊儲存方式使得運算能夠加速進行。古典電腦的位元並不具有這種量子糾纏的結構,因此計算總是局域性的。
這項研究重新定義了量子優勢的衡量標準,也驗證量子電腦在特定問題的計算能力確實有優勢。但這仍屬於理論上的突破,IBM科學家正積極的和實驗學家合作。若能在實驗上也能驗證量子優勢,計算科學才能算是真正進入量子時代。
[註1]: 量子電路的深度的定義是平均每個位元做運算的次數。
[註2]: 有興趣的讀者可以參考Bernstein-Vazirani problem。
參考資料:Sergey Bravyi et al., Quantum advantage with shallow circuits, Science 362, 6412, 308-311 (2018)
--
作者:陳奕廷,台大物理系學士,史丹佛大學應用物理系博士班就讀中。
