蘭道的典範之一：費米液體（二）

■為什麼準粒子假設會重要，而又有哪些物理不在費米液體的領域之內呢？

撰文｜蕭維翰

在上文中我們提供了一些歷史故事，希望提供讀者們一點探討一個標準教科書材料的理由。而在本文中繼續前文未完結的伏筆，並在最後稍稍討論有哪些已知的事實是已經超越「蘭道典範」。

我們首先複習蘭道費米液體的基本概念。在三維空間中，如果一個費米系統具有一個尖銳的費米面與伽利略對稱性，蘭道說明，在費米面附近的低能量自由度是一堆準粒子（quasi-particle）。假設準粒子間的交互作用是絕熱地被打開的，這些由準粒子定義的低能量物理激發態，跟完全沒有交互作用的費米氣體的能量激發態有一對一的對應關係。

準粒子間的交互作用，在蘭道費米液體理論中是由一堆現象學參數（phenomenological parameters）決定。這些參數在今日的教科書中稱為蘭道參數（Landau parameters）。物理上，他們正比於二個準粒子間的散射振幅。

首先大家可能會困惑，為什麼「準粒子」會是一個深刻的假設，畢竟我們在科普文章中，只要不是真的粒子，常常就會說這是準粒子。事實上，我們需要定量的資訊來決定這些有效的激發態是不是準粒子。

讓我們先想像，沒有交互作用的系統，也就是費米氣體。在這邊你有明確的粒子，因為某個粒子帶著明確的動量、能量、自旋或其他量子數在時空中旅行時，他基本上不跟任何人溝通，他不會因為碰撞等等過程散失它原來性質。

但，如果粒子間有交互作用，我們可以想像一個微觀的粒子，一開始帶有某些能量、動量。但因為跟其他粒子間有交互作用，當它在時空中穿梭，同時也會影響其他粒子，並且有機會因為碰撞過程，而失去原本定義它的性質（能量、動量等參數。）如果這個碰撞散射過程發生的時間尺度極短，那麼它就失去了「粒子」的特徵。

也因此，當我們考慮一個陌生的費米子強關聯系統，在沒有妥善計算的情況下，存不存在準粒子來描述低能量的物理沒有一個理所當然的答案—必須根據給定的交互作用，去計算問題中那些費米子的衰變率，如果這個衰變率在費米面附近足夠小，我們才能說這個問題中有妥善定義的準粒子。

更定量一點，如果一個費米子激發態的能量相對於費米能量為 ω，而衰變率為 Γ，要具有準粒子的資格，在費米面附近，至少要有

Γ~ω²

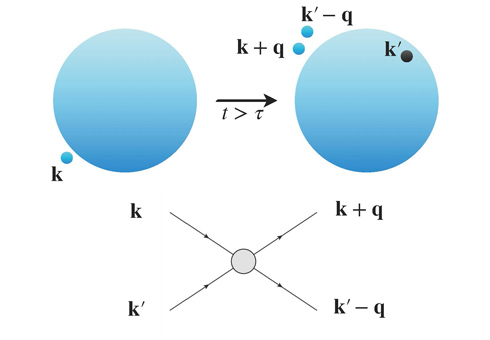
一個激發態的生命週期 τ 約略是衰變率的倒數 ，也因此上面的條件等同於

τ~1/ω²

在費米面上  ω→0，這個激發也因此有無窮大的生命週期，符合「粒子」的性質。如果是在有限的溫度下，則熱激發可以給予衰變率額外的貢獻

Γ'~ω²+Τ²

準粒子的存在，是蘭道費米液體的一個關鍵前提。這在晶格系統中不總是正確的， 一部分的原因是因為晶格系統不一定有足夠的對稱性。透過這樣簡單的假設加上以蘭道參數表示的交互作用能量，蘭道可以預測費米液體的有效質量、比熱、電荷響應等等性質—物理量的答案跟自由的費米氣體長得很像，只是整體的數值被蘭道參數「重整化」。

但要談到費米液體在當時真的新預測，就不得不提「零聲」（zeroth sound）。在一般的液體中，聲波是來自於液體的集體振盪。振盪的基本要件是回復力，也就是當一個粒子離開平衡位置的時候，必須要有一個力把它拉回原來的位置，這樣才可能產生振盪的現象。在古典的流體中，回復力透過粒子間的碰撞產生，也因此聲音是不存在極低溫的。然而在費米液體中，即便在低溫高頻的能量尺度，蘭道準粒子間的交互作用也提供了系統中的粒子密度產生回復力的機制，這種在無碰撞極限的聲音，稱之為零聲。

蘭道費米液體理論在液態 3He 中獲得極大的成功，同時也被作為描述一般金屬內電子的理論原型。前者與後者最大的差別在於，液態 3He 是電中性的，而後者是帶電的。不可避免我們便得討論它們的電性，譬如，我們是否能從費米液體理論計算一個材料的電阻值？答案是肯定的。並且可以從中推論，一個費米液體的電阻值應該正比於溫度的平方。

儘管獲得不小的成功，但費米液體的適用性，很大的依賴於維度、對稱與準粒子的存在性。從理論上看，在一維中有強交互作用的費米系統就不是費米液體。在霍爾效應中討論很多的負荷費米子液體，嚴格說來它們也都不適用費米液體描述。實驗上來看，近年來，人們開始找到一些新的強關聯系統，它們的電阻值在某些溫度的範圍，正比於溫度，而不是平方。即便這些發展促進了我們對不同維度強關聯系統的了解，但物理學家們卻還無法奠定下一個類似費米液體般典範性的框架—簡言之，半個世紀後的今天，我們依舊沒有完全走出蘭道的典範。

 

--
作者：蕭維翰，臺大物理系畢業後逃到芝加哥，吹風吹雪之餘，做研究讀博士班。可惜離開臺灣後無海可看，只能在密西根湖旁揀一方堤岸，偽裝成看海的人。科教中心特約寫手，從事科普文章寫作。