【摺紙專欄】摺紙設計基礎：等邊直角三角形分子

文/圖：台灣摺紙協會會員 林彥廷
電腦製圖：黃偵銘

分子這個名詞所代表的是摺紙設計中的一個基本結構，換句話說，一個摺紙作品的設計，是由複數個分子，經過排列組合而形成的，這一個組合成的分子群，就叫做基本型，基本型完成後，再藉由這一個基本型的分支，做分支聯想及摺疊嘗試，盡可能地呈現出個人對摺紙作品的藝術內涵及表達方式，以上所說的，就是摺紙設計的一個基本流程，我再做一次整理如下：

分子→複數分子的排列組合→基本型→聯想分支及摺疊嘗試→完成品

不要懷疑，所以的摺紙作品設計，都是以這樣一個流程為基礎做延伸及變化，你可能會說，自己或是看過某些高手，摺紙經歷數十年了，信手拈來都是創作，從沒聽過什麼分子設計。其實不盡然，因為這些高手只是用了而不自知。這些高手藉由經驗已經自然的將這些分子結構融入於摺疊中，而我所說的設計理論，則是從分析的角度來看待摺紙設計，這有何差別呢？差別可大了，前者需要有數年的摺紙經驗，才有辦法創作，後者只需要透過學習設計理論，就有辦法創作了，甚至是新手或小朋友，只要有心想創作得話，就一定有辦法設計得出來，透過學習設計理論，讓摺紙創作變得更簡單，變得人人都能夠創作，當然，就算學會了設計理論，也只是走創作這條路的開端。

接下來，就要從最簡單，也是最常用的一種分子開始說起，那就是等邊直角三角形分子。所謂的等邊直角三角形，我想大家應該都很熟悉，是由45ﾟ、45ﾟ及90ﾟ三個角所組成，如圖一1。分別在這三個角，做等角度的對折線，這三條對折線會交會於一點。任何三角形都一樣，所形成的圖形就是這個等邊直角三角形分子的分子結構，如圖一2。接下來在交會點與三個邊上，分別畫出三條垂直的虛線，如圖一3。我們以其中一個角為圓心，兩邊的垂直線交點為半徑，畫一個扇形出來，另外兩個角一樣，如圖一4。這個圖就是這個三角形分子的圓領域。何謂圓領域？圓領域就是將基本型的分支展開來後，分布在一張平面的紙上所佔的空間，觀察圖一4的三角形，可以算出這個三角形分子可以產生2個長分支和1個短分支，而分支的長度，就是這3個扇形的半徑我們將這3個半經，依照長度畫出來，就形成了樹狀圖，如圖一5。樹狀圖的定義就是將各分支的長度，用簡單的線條把它描繪出來。

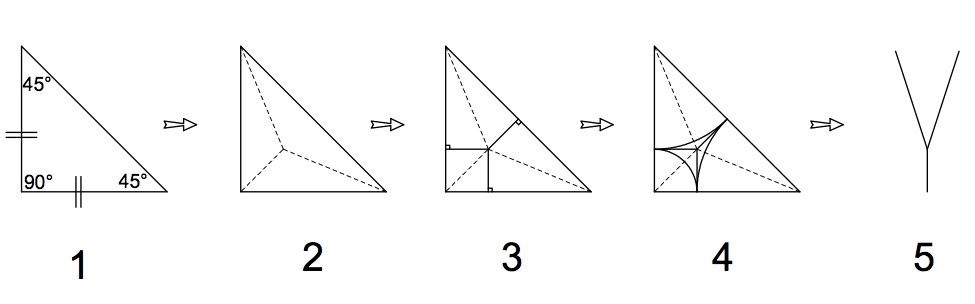
目前圖一的步驟，是屬於繪圖階段，接下來請拿出一張小張的紙(如便條紙)，實際上摺出圖一2的等邊直角三角形分子，如圖二1。

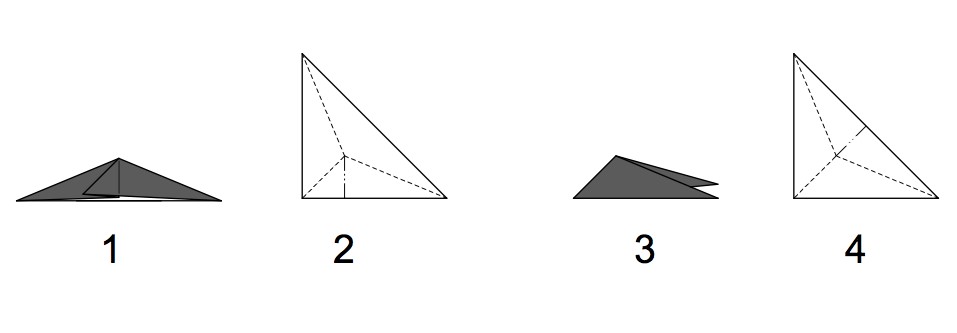
如果你真的想從這個方向學習設計的話，請真的實際上拿張紙出來摺，不要因為這只是個三角形分子，而忽略了這個動作，試著靠實際上的接觸來感受這一個三角形分子，用心去體會。這在學習設計的路上是個很重要的一個環節。把三角形摺出來(或剪出來)，把等角線摺出來，把等角線當摺痕直接闔上，觀察一下他的外型，試著與圖一所繪製的圖做結合，然後再把它給攤開。

讓我們在這裡停一下。觀察一下它的摺痕，和圖一2比較一下有何不同？如果你摺的三角形和圖二1一樣，那展開摺痕圖就會如圖二2，你會發現圖二2多一條谷線，如果你的的三角形如圖二3，那展開摺痕圖就會如圖二4，多的那條谷線位置會不一樣，我將這條谷線稱為可變式摺痕。再將這個三角形分子直接合起來，將三個分支個別左右都摺一下，再展開來，就形成了和圖一3一樣的摺痕。在這裡我們可以了解兩件事：第一，合起來的三角形分子，會因為分支方向的不同，而展開摺痕圖中，可變式摺痕的位置也會有所不同。第二，分子結構+可變式摺痕=展開摺痕圖。

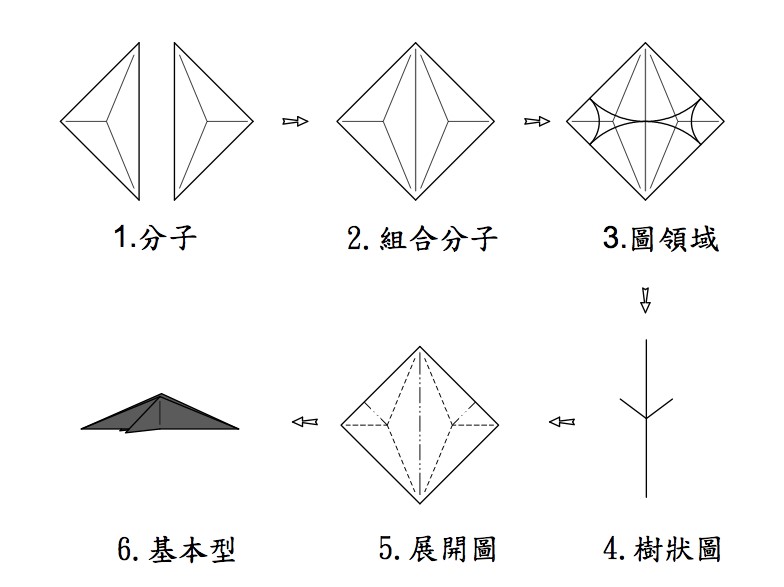
以上對等邊直角三角形分子的解釋，就告了一個段落，接下來就可以開始設計了，依照之前所強調的設計流程，接下來的步驟是「複數分子的排列組合」。我們就從最少數量的排列組合開始說起，那就是2個。我們將2個等邊直接三角形分子組合成一張正方型的紙，如圖三1，這樣子就完成了一個基本型的分子結構。你放心，這絕對不是最簡單的基本型，還有更簡單基本型存在。排列組合結束後，我們就來重複圖一3-5的過程，了解一下這個分子結構的圓領域和樹狀圖，如圖三2。確認這個基本型的分支數量為2長2短後，就可以開始摺製基本型了。不要管折疊的順序，把圖三1的線摺出來後，直接合起來，當然，在合起來的過程中，依照你所選擇的分支方向，一樣會產生出可變式摺痕，如圖三3，這樣就完成了一個基本型的設計及摺製。

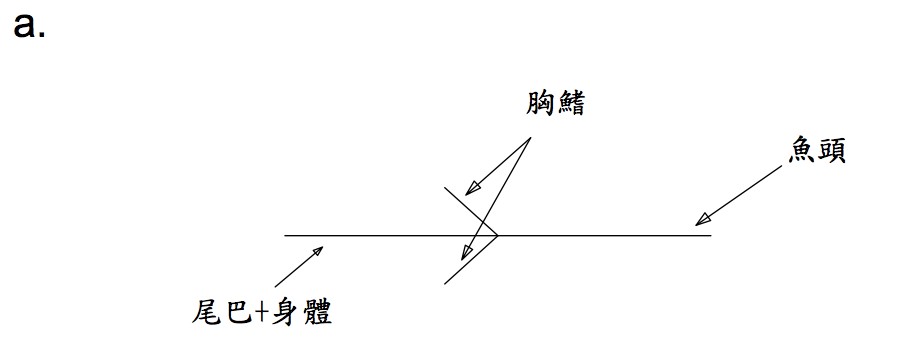
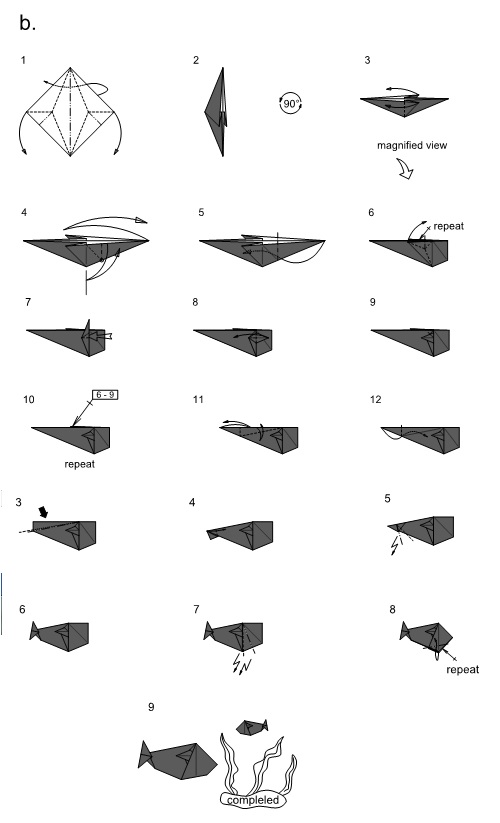
基本型完成了，接下來的步驟是「分支聯想及摺疊嘗試」，這是我覺得比較困難的一個階段，因為分支聯想需要創意靈感，而摺疊嘗試需要的則是經驗，聯想的部份，我們可以看著樹狀圖或實際摺製的基本型進行聯想。例如剛剛完成的基本型分支是2長2短，我把它聯想成一條魚，如圖四a。確定分支聯想後，就可以開始摺疊嘗試了，摺序如圖四b。摺疊嘗試的過程中，雖然非常依賴經驗，但是還有一個更重要的心理素質，那就是信心。你要相信你的分支聯想是絕對可以摺出來的，也絕對沒問題的，那就一定可以摺得出來。只要有信心，你會發現意外的驚喜會比想像中的還要多。有信心可以克服一切障礙。

了解了2個分子的排列組合及設計流程後，就可以嘗試的使用更多分子來進行排列組合了。設計流程就跟2個分子一樣。例如4個等邊直角三角形分子，如圖五1，8個等邊直角三角形分子，如圖五2。

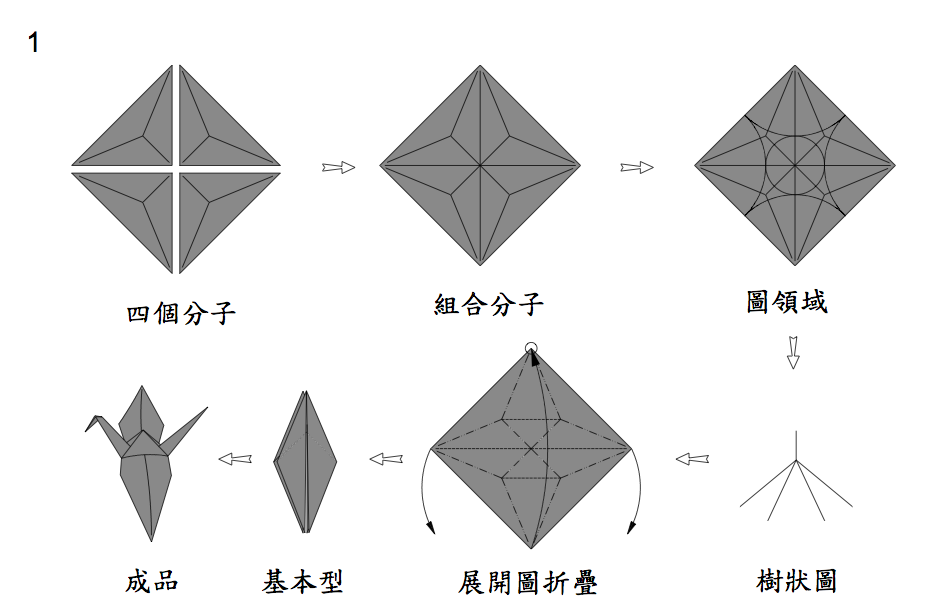
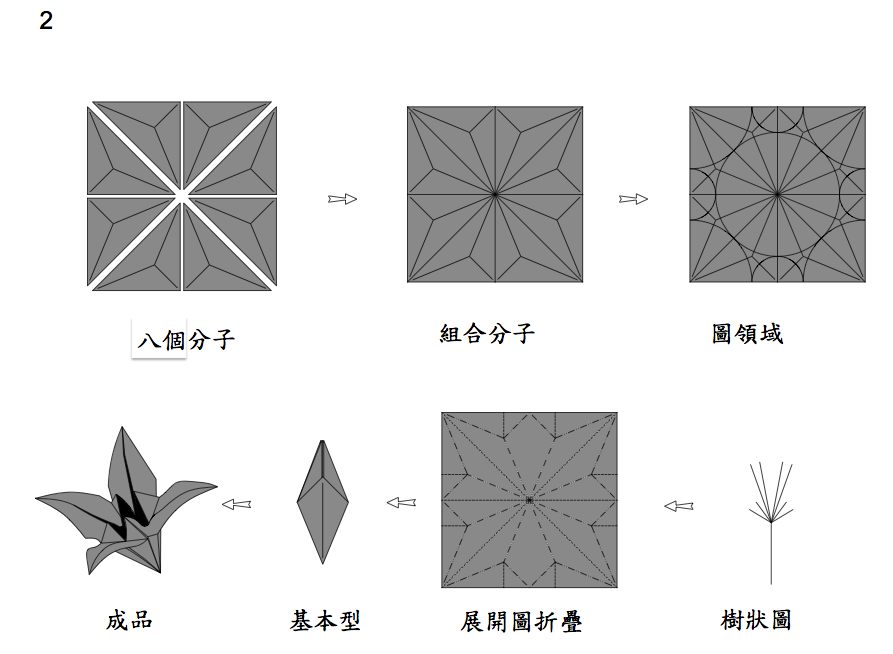
目前介紹到的這三個基本型，我想大家應該都很常見到，等邊直角三角形分子的排列，可以依照分支的需求來做變化及增加，受限於基本型的條件進行聯想，其實是一件非常困難的一件事，這也是創意的價值所在。雖然有很多東西沒辦法依照這些基本型，想摺就摺得出來，但是創意聯想卻是無限的。我在網路上就看過一名日本摺紙藝術家，利用一個鶴型基本型，就變化出上百種摺紙設計作品，實在是令人驚嘆。我想表達的是，摺紙藝術的價值並非取決於作品的複雜度，而是作品的內涵及表達方式。當然大家也不用擔心自己沒創意沒靈感，因為這等邊直角三角形只是多數分子中的一種，而分支聯想的設計方式，也只是眾多設計法的其中一種方式。只要繼續摸索，一定會找到適合自己的設計法。