【探索14-6】黑洞與量子力學：從霍京輻射到火墻悖論

講者｜北歐理論物理學研究所(NORDITA) 王元君研究員
撰文｜蕭維翰

21世紀第一個10年業已飛逝，百家爭鳴的歲月，若有人想對20世紀的物理學摘要論定，或許很難提出一個令所有學門分支滿意的結論 ; 然而，大概鮮少物理學家會否定「相對論與量子力學是20世紀以降物理學的兩大基石。」此一聲明。有趣的是，從它的斷句或多或少也能臆測此二架構並非相處得十分融洽，設想若在過去百年間，物理學家已清楚讓這兩個框架和諧共事的理路，今日此聲明大概會轉變為「某某理論是20世紀物理學的基石。」一如我們今日甚少特地區分「電學與磁學」而常稱呼「電磁學」、「電動力學」。

20世紀前中葉粒子物理幾乎集中所有心力在狹義相對論與量子理論的聯姻，在此基礎上物理學建構了人類史迄今最精確的理論之一，標準模型。令人沮喪的是，廣義相對論的量子化，相較於它的狹義表親，卻遲遲未見明朗。本講即著力於1970年以來學者嘗試在黑洞，即廣義相對論中的某種組態，考慮量子效應，所推論出的一系列悖論以及它們的合理解釋。

相對論是關於時、空間測量的理論。有了妥善的長度概念，物理學才有了有效的運動方程描述系統演化。在廣義相對論中，時空長度的概念被度規張量(metric tensor)定義，約略而言，給定了度規便有相對應的測地線方程(geodesic equation)描述粒子運動的狀態，而度規的動力學，或者說時空曲率(curvature)的分佈則透過愛因斯坦方程(Einstein field equation)決定，也就是惠勒(J. Wheeler)所言：「時空告訴物質如何運動，物質告訴時空如何彎曲。」

一點需要釐清的是，儘管度規定義了長度的概念，高中代數的經驗告訴我們即便在平直的空間，透過選定坐標系（如球坐標）也能使「長度」的樣子看起來很複雜，然時空彎曲的性質，也就是曲率的意義是內稟的(intrinsic)。 另外還有一點值得注意，上面的描述聽起來像並不牽涉特定物理現象，而是一個框架，但是在度規中其實包含了重力場的資訊，這透露了一點想法上套用舊有框架量子化重力的弔詭之處：原有的量子場論方法往往先具備明確的時空，進而描述各種場在時空中的演變，在重力的問題中，場即是時空本身 ; 換句話說，人類原來的習慣是找好了球場，再約球員們來打球，當球場地板也要一起打球時，乍聽之下自然令人不知所措。

在討論黑洞的量子效應前，先介紹古典黑洞的由來。1915年，愛因斯坦提出場方程式，史瓦西(K. Schwarzschild)。隨後不久即提出今日被稱為史瓦西度規(Schwarzschild metric)，此度規是原點以外真空愛因斯坦方程式的靜組態解。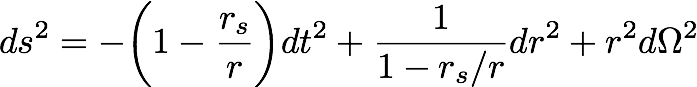

觀察此函數我們可以發現在 r = 0 與 r = rs 似乎都不是妥善定義的。但追及前段所言，度規的奇異點( singularity)可能肇因於坐標系的選擇，透過分析曲率與適當的坐標轉換，可以結論只有 r = 0 是真實的奇異點 ; r = rs 非但沒有發散現象，原點場源的質量愈大，該處感受的重力場甚至更微弱，自由下墜至此的觀察者，並不會感受到異狀。然而，該點依舊有其特殊性。在時空中每一點，原則上我們都可以研究光線的運動路徑，藉此描繪所謂的「光錐」，運動速率小於光的粒子，其時空軌跡便僅能被侷限在光錐之內。若我們留心去描繪 r = rs 附近的光徑，將發現 r < rs 範圍內的光錐都是朝內的，換句話說：墜入此區域的粒子，終將持續落向 r = 0 ，而無法脫離 ; 即便無質量的粒子能沿著光錐行進，也至多能沿著邊界運動，無力奪門而出。這便是最簡單的黑洞組態，rs被稱為黑洞的視界。

接著我們嘗試討論量子效應。一如前言所述，量子化重力乍聽之下並不直觀。也的確，量子重力理論迄今尚未有完善的結論 ; 是以，此處的量子效應的層次是將在平直時空中已有充分了解的量子場（如介子場）建立在備有符合愛因斯坦方程式的古典度規上。大致上量子場論是可以任意曲線坐標構造的，作為暖身習作，我們可以先考慮平直的時空背景，但選用不同的坐標去描述，並在兩坐標間分別定義場論：透過計算人們發現得到即便在平直的時空，靜止者所觀察到的「真空」在等加速度的觀察者眼中充滿粒子的，並且粒子這些粒子會形成熱分佈，該分佈的溫度正比於加速度的量值，此效應稱為盎魯效應(Unruh Effect)。在認識此效應後，讀者大概就比較不意外，在史瓦西度規的背景下，量子效應使得黑洞輻射出粒子，甚至這些粒子的頻譜定義了一溫度，此效應稱為霍京輻射(Hawking Radiation)，該溫度則稱為霍京溫度(Hawking temperature)

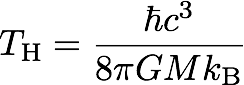並且因為輻射減少了能量，黑洞終將揮發並消失。

作為事後諸葛，從場論的觀點，此二效應並非真的驚世駭俗。量子場論允許粒子從真空中產生，在有外加能量源的狀況下，真空生出的粒子甚至不必要湮滅而可以持續存在乃至于讓實驗觀測。例如我們可以考慮一外加強電場的系統，量子場論預測在電場足夠強大的狀況下，「真空」有一定的機率衰變成具有粒子存在的狀態，此效應稱為施溫格效應(Schwinger Effect )。以較量子力學的語言來闡述，在無窮遠的未來與過去我們都小心地定義了「真空」，若在未來與過去間某段時間我們打開外加的電場，過去的真空在未來的人眼中便不再是「真空」，而是充滿粒子的。「真空」的意義隨著觀察者不同而有改變。類似的觀點可以套用在霍京輻射的現象，由於在無窮遠的未來與過去間，有物質塌陷等重力場的擾動，因而在無窮遠未來與過去的觀察者定義出不同的「真空」，在未來觀察者的眼裡，他將量測到粒子。當然前揭的討論只是躲在代數後的理解，並沒有妥善去解釋粒子產生的機制等問題，一般來說，讀者可以想像正反粒子對因為量子擾動產生，其中一者遂入黑洞，另一者則往觀察者行進。

更困擾物理學家的是，霍京輻射導致的推論。若初始的星系被一個量子純態(pure state)描述，經歷霍京輻射形成熱分佈，該系統將處於混態(mixed state)現有量子力學的架構中一個純態透過么正算子(unitary operator)進行時間演化，由將為純態，原則上我們有反推時間演化解析原來狀態的能力。若霍京輻射最後真的形成混態，某種程度上意指在時間演化過程中，資訊喪失，這即是所謂的資訊喪失悖論( information loss paradox )。最有名的例子當屬霍京、索恩(K. Thorne)和 J. Preskill 的賭約：若將一本百科全書擲入黑洞，是否能重建這本書的資訊呢？現代高能物理中有一概念稱為「規範-重力」對偶(gauge/gravity duality)，此對偶性的大致意涵是某些古典的重力理論存在著一個量子場論的對應，後者是符合么正性的(unitarity)，即在此類理論中，純態經歷演化依舊是純態，若此對偶性總是嚴格為真的，那對應的黑洞解也不應該丟失資訊。目前大多數學者也開始相信資訊並未因黑洞而流失，倘若如此，那提取這些資訊的方法又是什麼？目前較為人接受的是 D. Page 的說法，透過量子糾纏，霍京輻射可帶有資訊，透過計算 Page 也定義了一個時間尺度 Page time，在此時間以前，整個黑洞的糾纏熵（entanglement entropy，用於定量說明量子糾纏程度的大小）增加。而在之後，糾纏熵減少，資訊也在後半段被提取出來。

2004年霍京表示經過新的計算，他認為資訊沒有喪失在黑洞中，並依賭約致贈Preskill一套百科全書，黑洞戰爭似乎在二十一世紀初偃兵息甲。然而，A. Almheiri、D. Marolf、J. Polchinski 和 J. Sully在 2012 年提出：對於夠老的黑洞 (1) 霍京輻射不喪失訊息，(2) 遠處觀察者所處的漸進平直時空可定義量子場論描述物理，(3) 落入黑洞的觀察者在視界上並沒有感受到異狀（no drama），此三論述是不能同時成立的。從資訊的角度來談，若資訊沒有遺失，則 Page 的論證要求 Page time 之前的輻射跟後期的輻射是完全糾纏的，另一方面，若自由下墜的觀察者沒有感受到異狀，則要求輻射的粒子與掉入黑洞的粒子是完全糾纏的，這兩類糾纏會違反量子力學中糾纏熵總和的不等式，該文中指出，從 (1) 與 (2) 可以推論，因重力藍移，在下墜觀察者的坐標系他所觀測到的將是極高頻的輻射，也就是火牆（ firewall ）。 AMPS 是以結論：若火牆存在，則 no drama 被違背，進而相對論的觀念基礎「等效原理」(equivalence principle)受到挑戰 ; 若不存在火牆，則資訊終究在黑洞中遺失，或者現有的量子場論是需要修正的，放棄三者中任意一項都將對現在物理學造成震撼。

迄今關於火牆持續有學說被提出，但尚未有一公認的解釋。某些學者認為黑洞並不會完全揮發，而有資訊會儲存在殘骸之中 ; 色斯金( L. Susskind)則提出所謂 ER = EPR 的概念，大意為掉入黑洞內的粒子與早期被輻射出的粒子可經由蟲洞相關聯，從而去規避導致火牆的熵不等式 ; 亦有學者如賀培銘教授從模型進行修正，考慮物質在塌縮成黑洞前便開始進行輻射，從而可以計算藍移頻率的上界，推論火牆的不存在。

霍京輻射問世亦已40年，經歷近半個世紀，從疑惑黑洞並非純黑、到擔心黑洞湮滅資訊，直至今日震懾於黑洞不但發光，更甚至有一道火牆，或許我們真正了解的僅是，同時馴服黑洞與量子力學的方法，只可能比多數人預期的更加顛覆想像。

參考資料：
1. Zee, Einstein’s Relativity in a Nutshell
2. Carroll, Spacetime and Geometry - An Introduction to General Relativity
3. Wald, Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics
4. Mathur, The Information Paradox, A Pedagogical Introduction
5. D. Page, Time Dependence of Hawking Radiation Entropy
6. Almheiri, D. Marolf, J. Polchinski, and J. Sully, Black Holes: Complementarity or Firewalls?
7. L. Susskind, ER=EPR, GHZ, and the Consistency of Quantum Measurements
8. P. M. Ho, Comment on Self-Consistent Model of Black Hole Formation and Evaporation

--
本文整理自：104/12/5由王元君研究員在臺大應力所國際演講廳所主講之「黑洞與量子力學：從霍京輻射到火墻悖論」演講內容。