【大宇宙小故事】52 愛因斯坦─波耳論戰(上)
撰文|葉李華
愛因斯坦七十大壽時收到一份很別緻的生日禮物,一本由25位學者合寫的文集,書名是《亞伯特‧愛因斯坦:哲學家─科學家》。其中最長的一篇〈與愛因斯坦討論原子物理中一些認識論問題〉出自老友波耳之手,為兩人多年來針對量子力學的爭辯提供了重要史料。
眾所皆知,這兩位大師雖然私交甚篤,在這個問題上卻勢同水火,因此「愛因斯坦─波耳論戰」早已是物理學史上的專有名詞。根據波耳的回憶,這場論戰大致分成三個回合,時間分別是1927年、1930年以及1935年。不過在這篇長達四十頁半的文章中,波耳主要是在探討學術問題,很少觸及兩人亦敵亦友的微妙關係。好在這三回合皆可算是公開賽,有不少目擊者的記述能彌補這個遺憾。
●第一回合◎時間:1927年十月◎地點:比利時首都布魯塞爾◎場合:第五屆索爾維會議
這場學術會議在科學史上佔有重要地位,甚至有人將它視為量子力學的分水嶺,認為哥本哈根學派在這場會議中大獲全勝,搖身一變從非主流躍升為主流。不過事實當然沒有那麼簡單,我們頂多只能說,哥本哈根學派的表現讓同行留下深刻印象,但距離真正發酵還有一段時間。

另一方面,愛因斯坦個人倒是在這場盛會中吃了不少虧,不過並非在正式會議中,而是屬於「會外賽」的性質。這方面,我們有海森堡的第一手回憶:
「我們通常在旅館吃早餐時就聚在一起,愛因斯坦開始描述某個想像實驗,用以突顯哥本哈根詮釋的內在矛盾。然後,我陪著波耳和愛因斯坦從旅館步行到會議廳,一路上聆聽兩人生動的討論,他們的哲學觀差了十萬八千里。偶爾,我會針對數學部分提些意見。上午每逢空檔,我們幾個年輕人(主要是包立和我自己)會試著分析愛因斯坦提出的實驗,到了午餐時間,波耳和其他哥本哈根成員也會繼續討論。通常接近傍晚時,波耳就會把當天的問題分析透澈,然後藉著晚餐的機會跟愛因斯坦攤牌。愛因斯坦總是難以駁斥,不過並沒有真正被說服。」
總而言之,對於愛因斯坦發動的攻勢,波耳每次都能見招拆招,不但讓對手鎩羽而歸,還因此擄獲不少人心。最明顯的例子,就是和他倆都有多年交情的埃倫費斯特(Paul Ehrenfest)也開始批評愛氏過分保守:「羞不羞啊,愛因斯坦,你跟當年反對相對論那些人沒兩樣了!」
■物理解析
為了便於說明,我們把這回合最精采的過招濃縮成兩個圖解。這麼做雖不算完全忠於史實,但至少掌握了關鍵的精神。
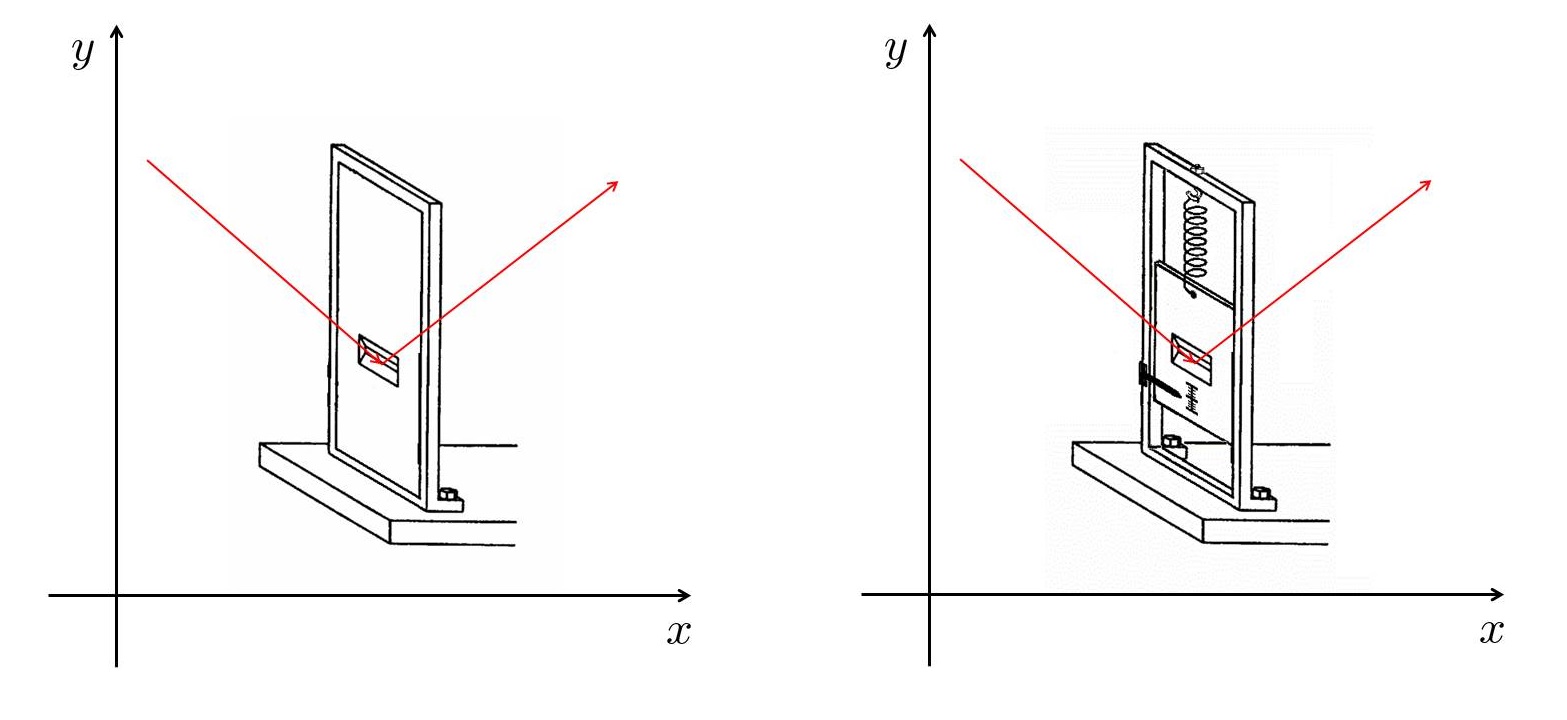
愛因斯坦的論述(左圖):如果我們觀測到有個光子穿過狹縫,就能確定在穿越的一瞬間,光子的y座標一定在狹縫範圍內。狹縫如果越小,這個y值就越準確,而且這個準確度可以盡量提升。
另一方面,只要光子不是平行穿過狹縫,就有可能被狹縫邊緣反彈。在反彈過程中,光子的y方向動量一定會反轉(例如從向下變成向上)。根據牛頓第三運動定律,狹縫邊緣會感受到這個變化,因此光子的y方向動量可以用狹縫裝置測量出來,而這個測量的準確度也沒有先天的限制。
總之,在光子穿越狹縫的瞬間,它的y方向位置和動量能夠各別被測得很準。兩者的準確度一來沒有上限,二來不會互相影響,這就代表△q*△p~h這個關係在此並不成立。
波耳的反駁(右圖):想要利用狹縫裝置測量動量,必須設法讓它具有彈性,例如掛在一個彈簧秤上。一個硬邦邦的裝置等於具有無限大的質量,不可能感受到動量的變化。可是一旦狹縫裝置有了彈性,一定會在光子反彈時上下移動,無法準確測量光子當時的y座標。
想要提升位置的準確度,就要限制彈簧的伸縮量,這就等於降低彈簧秤的精密度,導致動量的準確度下降。反之,若想提升動量的準確度,就要提高彈簧秤的精密度,這就會使得彈簧的伸縮量變大,導致位置的準確度下降。
由此可知,在這個想像實驗中,「位置的準確度」反比於「動量的準確度」,剛好符合測不準原理的精神。

●第二回合◎時間:1930年十月◎地點:同上◎場合:第六屆索爾維會議
俗語說君子報仇三年不晚,第六屆索爾維會議於三年後按時召開,愛因斯坦打定主意要一雪前恥。於是波耳又跟有備而來的愛氏打了一場會外賽,主題仍是測不準原理。至於幕後花絮,這回要仰賴波耳的助理羅森菲爾德(Léon Rosenfeld),他大致是這麼說的:
「這次愛因斯坦提出的是光箱實驗,光箱在特定時刻釋放一顆光子,我們只要測量光箱的質量變化,便能確定那顆光子的能量,愛氏認為這就構成了測不準原理的反例。
「這個難題讓波耳相當震驚,他當下並未看出任何破綻。晚餐時間波耳一直惴惴不安,他在眾人面前走來走去,試著說服大家別輕易相信;如果愛因斯坦正確,物理學可就完蛋了──偏偏他又無法提出辯駁。我永遠忘不了這對敵手走出餐廳的情景:愛因斯坦高大威嚴,步履輕盈,臉上掛著幾分嘲諷的笑容;波耳小跑步跟在他旁邊,顯得非常激動,一再強調愛氏不可能正確,否則物理末日近在眼前。
「第二天早上,波耳得意洋洋地宣布物理學得救了,他找到了愛氏的破綻:當我們測量光箱質量時,(根據廣義相對論)光箱在重力場中的位移會改變時鐘的頻率,導致它無法準確控制釋放光子的時間,這個不準度剛好符合測不準原理。」
由此可知,波耳反敗為勝的關鍵正是愛因斯坦自己的成名招式!當這場論戰廣為流傳後,人人都忍不住為波耳鼓掌喝采。這無異於現代版的「以子之矛,攻子之盾」,不過或許「以彼之道,還施彼身」這八個字是更貼切的形容。
■物理解析
這場辯論的物理內容可以比較忠實地解說如下:
愛因斯坦的論述:我們可以製造一個精密的箱子,將固定數量的光子封存在裡面。箱子上的閘門能夠精確控制開關的時間,讓我們在某個瞬間剛好放出一個光子。閘門開關如果越精密,就能將光子飛走的時間測得越準確,而且這個準確度可以盡量提升。
另一方面,根據狹義相對論的質能等價關係(E=mc2),在光子飛走後,光箱的質量會稍微減少。只要利用彈簧秤,我們就能測量光箱釋放光子前後的質量差,進而推算那個光子的能量。這意味著光子的能量可以用彈簧秤測量出來,而這個測量的準確度也沒有先天的限制。
因此「光子飛走的時間」和「光子的能量」能夠各別被測得很準,兩者的準確度一來沒有上限,二來不會互相影響,這就代表△t*△E~h這個關係在此並不成立。
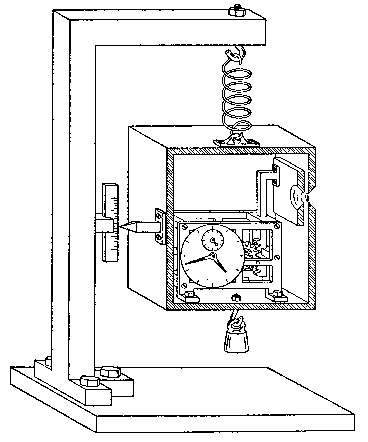
波耳的反駁:在這個想像實驗中,愛因斯坦最大的失誤是忘了考慮廣義相對論。根據狹義相對論,時間會受到速度的影響,這就是著名的時間膨脹效應,大致可以說成「運動中的時鐘走得比較慢」。事實上,廣義相對論中也有類似的效應,白話的說法是「重力場會把時鐘拉慢」。因此在強度不同的重力場中,時鐘的「轉速」會有所不同。
我們之所以能用彈簧秤或天平測量光箱的質量,正是因為光箱置身於地球的重力場中。地表附近的重力場雖然大致可以視為均勻,但嚴格說來強度會隨著高度遞減。因此之故,當光箱釋放光子因而質量減少時,彈簧秤的彈簧會稍微收縮,使得光箱升高一點點,於是其中的時鐘會在這一瞬間稍微變快,導致時間測量上的不準度。如果我們改用天平,同樣會出現類似的情形。
想要提升時間的準確度,就要限制彈簧的伸縮量,這就等於降低彈簧秤的精密度,導致質量差(亦即光子能量)的準確度下降。反之,若想提升光子能量的準確度,就要提高彈簧秤的精密度,這就會使得彈簧的伸縮量變大,導致時間的準確度下降。
由此可知,在這個想像實驗中,「時間的準確度」反比於「能量的準確度」,剛好符合△t*△E~h的精神。看到這裡,想必大家已經發覺這兩回合有著微妙的平行關係。
* * *
雖然連吃兩場敗仗,愛因斯坦仍舊相信真理站在自己這邊,波耳只是利用小聰明,加上一點運氣,一時之間佔了上風罷了。等著吧,老夫終將捲土重來……
