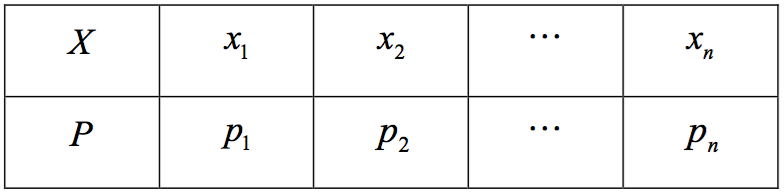線性規劃(Linear Programming)
臺北市立第一女子中學數學科蘇俊鴻老師

讓我們就從下面的例子說起，來介紹什麼是線性規劃：

為預防禽流感，營養師吩咐雞場主人每天必須從飼料中提供至少 84 單位的營養素 A 、
至少 72 單位的營養素 B 和至少 60 單位的營養素 C 給他的雞群。

這三種營養素可由兩種飼料中獲得，且知第一種飼料每公斤售價 5 元並含有 7 單位的營 養素 A ，3 單位的營養素 B 與 3 單位的營養素 C ；第二種飼料每公斤售價 4 元並含有 2 單位的營養素 A ， 6 單位的營養素 B 與 2 單位的營養素 C 。

若雞場主人每天使用 x 公斤的第一種飼料與 y 公斤的第二種飼料就能符合營養師吩咐，並且想以最少的飼料成本來達到雞群的營養要求，則x, y 的值為何？最少的飼料成本又是多少？

換言之，雞場主人想要以「最少」的飼料成本來達成雞群的營養要求，以達到預防禽流感的目的；將成本寫成算式，就稱為目標函數。

該如何配置這兩種飼料的使用？首先，我們當然要先了解各種條件的限制。若是依條件列出的算式，以及「目標函數」都是一次式，我們就將此類的問題稱為「線性規劃」。

以上述問題來看，設每天使用第一種飼料 \(x\) 公斤；第二種飼料 \(y\) 公斤，

將條件列出，可得二元一次聯立不等式 \(\left\{ \begin{array}{l} x \ge 0,y \ge 0\\ 7x + 2y \ge 84\\ x + 2y \ge 24\\ 3x + 2y \ge 60 \end{array} \right.\) 。

同時，目標函數(即飼料成本)為 \(5x+4y\) 。這個問題便是典型的線性規劃問題。

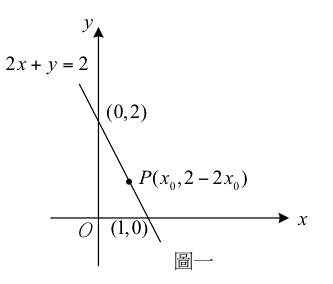
進而，我們將滿足聯立不等式的解區域畫出，稱為可行解區域，如圖一。 Continue reading →

二元一次不等式(Two-Variable Inequalities)
臺北市立第一女子中學數學科蘇俊鴻老師

若 $$a,b,c$$ 為實數，且 $$a,b$$ 不同時為0，則稱 $$ax+by+c=0$$ 為二元一次方程式；

又因為它的圖形為一直線，也稱為直線方程式。

圖一正是二元一次方程式 $$2x+y=2$$ 的圖形。事實上，直線 $$2x+y=2$$ 上的任一點，

其坐標 $$(x,y)$$ 都滿足方程式 $$2x+y=2$$，換言之，都是方程式 $$2x+y=2$$ 的解。

因此，當點 $$P$$ 的 $$x$$ 坐標為 $$x_0$$ ，易推得 $$y$$ 坐標為 $$2-2x_0$$ 。

Continue reading →

數學期望值 (Mathematical Expectation)
國立屏東高級中學數學科楊瓊茹老師

在處理有關財務風險的事務時，不免要衡量可能的得與失，「數學期望值」的觀念在此時就顯得特別重要，可以幫助我們思考及判斷出最佳的決策。其定義如下：

若隨機變數 \(X\) 的機率分布如下表﹕

則稱 \(E\left( X \right) = {x_1}{p_1} + {x_2}{p_2} + \cdots + {x_n}{p_n} = \sum\limits_{i = 1}^n {{x_i}{p_i}} \) 為隨機變數 \(X\) 的數學期望值。

數學期望值 (簡稱期望值) 即平均值的概念，而且是加權平均數。將每個結果依它發生的機率來加權，發生機率愈大，權數愈高。 Continue reading →

機率法則 (Principle of Probability) (二)
國立屏東高級中學數學科楊瓊茹老師

連結：機率法則 (Principle of Probability) (一)

1993年美國奧克拉荷馬州突沙市 (Tulsa, Oklahoma) 法庭根據DNA鑑定報告等相關證物，判決提摩西‧杜朗犯下強暴與強盜罪。即便有十一個證人作證在案發時，提摩西正在達拉斯州參加飛靶射擊比賽，但是犯罪現場採得的DNA卻與提摩西的DNA吻合，在這項強力的證據下，求處刑期3200年。

究竟DNA鑑定比對的準確率有多高？高達 $$999,999/1,000,000$$ ！隨便一個人的DNA與犯罪現場的採樣相同的機率小於百萬分之一，甚至是億萬分之一，相同的可能性可以說是微乎其微。 Continue reading →

機率法則 (Principle of Probability) (一)
國立屏東高級中學數學科楊瓊茹老師

由拉普拉斯古典機率定義 $$P(A) = \frac{{n(A)}}{{n(S)}}$$，我們推得下列的基本法則：

若 $$A$$、$$B$$為兩事件，則

1.  $$0 \le P(A \cap B) \le P(A)$$，$$0 \le P(A \cap B) \le P(B)$$ 。
2.  $$P(A \cup B) = P(A) + P(B) – P(A \cap B)$$。
3. 當 $$A$$ 與 $$B$$ 為獨立事件時，$$P(A \cap B) = P(A) \cdot P(B)$$；
   當 $$A$$ 與 $$B$$ 為互斥事件時，$$P(A \cup B) = P(A) + P(B)$$。 Continue reading →
4. 牛頓法 ( Newton’s Method ) 2014/01/18

   牛頓法 ( Newton’s Method )
   國立屏東高級中學數學科楊瓊茹老師

   在2008年上映的美國電影《決勝21點》中，教授米奇 (Mickey Rosa) 請同學們解釋「牛頓法」及其應用，此時班 ( Ben Campbell ) 卻語出驚人說：「牛頓剽竊了拉福生的方法。」

   站在巨人肩上的牛頓是剽竊者？這是真的嗎？

   所謂的「牛頓法」( Newton’s Method ) 是指求解方程式 \(f(x)=0\) 的根之疊代法 (Iterative Method)，又稱為「牛頓–拉福生演算法」( Newton-Raphson Algorithm)。 Continue reading →

5. 轉移矩陣的穩定狀態與Google搜尋引擎 2014/01/18

   轉移矩陣的穩定狀態與Google搜尋引擎 (The Stationary of a Transition Matrix, and Google Search)
   國立臺南第一高級中學數學科林倉億老師

   

   若 \(n\) 階方陣 \(M = {\left[ {{a_{i{\kern 1pt} j}}} \right]_{\;n \times n}}\) 滿足：

                            (1) 每個 \(a_{ij}\) 都滿足 \(0\leq a_{ij}\leq 1\) ；

                            (2) 每行的各元之和為1。

   我們就稱 \(M\) 為「 \(n\) 階轉移矩陣」，簡稱為「轉移矩陣」。

   多找幾個轉移矩陣來試試，就會發現有些矩陣不管初始狀態 \(X_0\) 為何，隨著 \(n\) 越來越大，

   \(M^nX\) 就會越來越趨近於某個 \(X\)。 Continue reading →

6. 轉移矩陣（Transition Matrix） 2014/01/16

   轉移矩陣（Transition Matrix）
   國立臺南第一高級中學數學科林倉億老師

   「轉移矩陣」的概念是由俄國數學家馬可夫 (Andrei Andreevich Markov, 1856~1922)在20世紀初時所提出，今日不管是在科學界、工程界還是商業界，都有很廣泛的應用，因此，我們又將「轉移矩陣」稱為「馬可夫矩陣」。讓我們從一個實際例子來了解什麼是「轉移矩陣」。

   假設今天在郊區有個住宅區，居民每天可任意選擇自行開車上班，或搭乘大眾運輸工具上班。長期觀察此區的居民，發現當天開車上班的人中，有 \(\frac{4}{5}\) 的人隔天會繼續開車，另外的 \(\frac{1}{5}\) 會改搭大眾運輸工具；而當天搭乘大眾運輸工具的人中，有 \(\frac{2}{5}\) 的人隔天會繼續搭乘，但有  \(\frac{3}{5}\) 的人會改為自行開車。倘若我們是當地的交通主管官員，當看到這樣子的數據時，我們可以做出何種預測呢？預測正確，我們所做的決策才不會有問題。 Continue reading →