牛頓插值多項式 (3) (Newton Interpolating polynomial)
臺北市立第一女子高級中學蘇俊鴻老師

連結：牛頓插值多項式(2)

在〈牛頓插值多項式(2)〉中，我們討論了牛頓插值多項式形式的意義。接下來，我們想要介紹數值分析中對於牛頓插值多項式中各項係數的運算規則和簡便求法。基本上，它的思路和〈牛頓插值多項式(2)〉中所談論的想法一致，只是我們透過符號的輔助，幫助掌握其中所涉及的規律。我們的問題為

給定 \(n+1\) 個資料點 \(({x_0},f({x_0})),({x_1},f({x_1})),({x_2},f({x_2})), \cdots ,({x_n},f({x_n}))\)，
求滿足這 \(n+1\) 個資料點的 \(n\) 次多項式 \(f(x)\)。

首先，從滿足兩個點 \(({x_0},f({x_0})),({x_1},f({x_1}))\) 的一次多項式 \(f_1(x)\) 討論起。

假設 \({f_1}(x) = f({x_0}) + {b_1}(x – {x_0})\)

那麼，\({f_1}({x_1}) = f({x_1}) = f({x_0}) + {b_0}({x_1} – {x_0}) \Rightarrow {b_1} = \frac{{f({x_1}) – f({x_0})}}{{{x_1} – {x_0}}}\)。

因此 \({f_1}(x) = f({x_0}) + \frac{{f({x_1}) – f({x_0})}}{{{x_1} – {x_0}}}(x – {x_0})\)

接著，考慮滿足三個點 \(({x_0},f({x_0})),({x_1},f({x_1})),({x_2},f({x_2}))\) 的二次多項式 \(f_2(x)\)。

承上面的結果，可以假設

\(\begin{array}{ll}{f_2}(x) &= {f_1}(x) + {b_2}(x – {x_0})(x – {x_1}) \\&= f({x_0}) + \frac{{f({x_1}) – f({x_0})}}{{{x_1} – {x_0}}}(x – {x_0}) + {b_2}(x – {x_0})(x – {x_1})\end{array}\)

Continue reading →

牛頓插值多項式 (2) (Newton Interpolating polynomial)
臺北市立第一女子高級中學蘇俊鴻老師

連結：牛頓插值多項式(1)

一樣從這個問題開始

給定平面上三點 \(A(1,7)\)，\(B(2,6)\) ，\(C(3,11)\)，求圖形通過這三點的二次多項式。

我們知道基於牛頓插值多項式，可以假設所求函數 \(f(x)\)為

\(f(x) = f(1) + a(x – 1) + b(x – 1)(x – 2)\)

通常開頭這個形式就是初學者亟需跨越的門檻。本文試圖利用學生已經擁有的多項式知識，提供一個教學上可行的引導，尚請方家不吝指教。至於學生需要知道什麼多項式的知識呢？只要因式定理即可。

Continue reading →

牛頓插值多項式 (1) (Newton Interpolating polynomial)
臺北市立第一女子高級中學蘇俊鴻老師

由於多項式「常被用來逼近一般函數，並用來求一般函數的近似值。」，使得插值多項式有了學習的正當性，99課綱並特意引進拉格朗日插值多項式。

例如：以給定平面上三點 \(A(1,7),B(2,6),C(3,11)\) 為例，求圖形通過這三點的二次多項式。上述的問題等同於求一個二次多項函數 \(f(x)\)，使得 \(f(1)=7,f(2)=6,f(3)=11\)。

那麼，滿足條件的拉格朗日插值多項式為

\(\displaystyle f(x) = 7 \cdot \frac{{(x – 2)(x – 3)}}{{(1 – 2)(1 – 3)}} + 6 \cdot \frac{{(x – 1)(x – 3)}}{{(2 – 1)(2 – 3)}} + 11 \cdot \frac{{(x – 1)(x – 2)}}{{(3 – 1)(3 – 2)}}\)。

然而，許多課本還加碼補充牛頓插值多項式的方法（這也說明有著各種不同形式的插值多項式）。

通常開頭就會寫道：假設基於牛頓插值多項式，

滿足條件之函數 \(f(x)=f(1)+a(x-1)+b(x-1)(x-2)\)，

再將 \(f(2)=6,f(3)=11\) 代入，求出 \(a,b\)。

事實上，這樣的補充留下的問題，比它所解決的問題還多。例如，為何牛頓插值多項式會是上述的形式？除了背誦記憶規則外，有沒有理解它的其他方法？牛頓插值多項式的假設仍需要再求解未知數，會比拉格朗日插值多項式便利嗎？這個方法最早是牛頓給出的嗎？他如何想到的？是為了解決什麼問題呢？這個系列文章就是想要解答以上這些問題。首先，就由牛頓開始吧！ Continue reading →

橢圓平行弦中點共線問題
（Collinearity Problem on the Midpoints of Parallel Chords of an Ellipse）
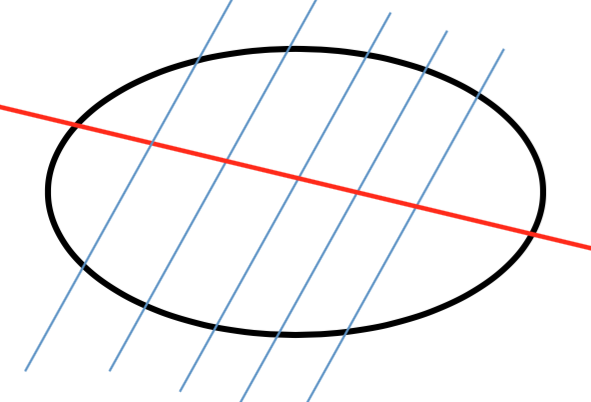
臺北市立和平高中黃俊瑋教師

高中圓錐曲線單元裡，一個常見的延伸問題如下：在橢圓  \(\Gamma :\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) 內所有斜率為 \(2\) 的平行弦，已知這些弦的中點共線，請問其所在直線方程式為何（參見圖一）？

換言之，本問題相當於：已知直線 \(y = 2x + k\) 與 \(\Gamma :\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) 相截於兩點 \(A,B\)，當參數 \(k\) 變動時，求 \(A\) 與 \(B\) 之中點 \(M(x,y)\) 的軌跡所在直線方程式。

圖一\(~~~\)斜率為 \(m\) 的平行弦中點軌跡所在圖形

Continue reading →

條件句與對偶命題 (Conditional and contrapositive statements)
臺北市立和平高中黃俊瑋教師

在數學上，有許多敘述句皆具有下列形式：\(P\) 蘊涵 \(Q\)

而它的意義即為：若 \(P\) 為真，則 \(Q\) 也必須為真 

此外，尚包含了其它與蘊涵相關的術語，例如：若 \(P\) 則 \(Q\) 、\(P\) 是 \(Q\) 的充分條件、\(P\) 唯若 \(Q\)、\(Q\) 若 \(P\) 以及 \(Q\) 是 \(P\) 的必要條件等，而這些術語的意義皆相同。例如，「若 \(n^2\) 為偶數，則 \(n\) 為偶數」、「若 \(x\) 與 \(y\) 皆為有理數，則 \(x+y\) 為有理數」以及「若 \(\Delta ABC\) 為直角三角形，則斜邊平方等於兩股之平方和」等，都是此類具蘊涵關係的敘述句。

一般而言，蘊涵關係包含了涉及真值（truth）的條件句與因果關係（causation）兩部份，我們以符號「\(P \Rightarrow Q\)」來表示 \(P\) 蘊涵 \(Q\) 的真值部份，並把具「\(P \Rightarrow Q\)」這種形式的句子，稱為條件表達式或簡稱為條件句。其中 \(P\) 的稱為前項或前件（antecedent）， \(Q\) 則稱為後項或後件（consequent）。 Continue reading →

西方行列式的發展：結語
（The Development of Determinants in West: Concluding Remarks）
國立臺南第一高級中學林倉億老師

連結：西方行列式的發展：柯西的研究

行列式在西方萌芽後，在數學家們辛勤地澆灌、耕耘下，歷經了100多年，終於成熟。為行列式發展做出的數學家很多，〈西方行列式的發展〉系列文章只挑選了其中幾位作簡要的介紹，其他未寫到的數學家如拉格朗日 (Joseph Lagrange, 1736-1813)、拉普拉斯 (Pierre-Simon marquis de Laplace, 1749-1827)、比內 (Jacques Philippe Marie Binet, 1786-1856)、雅可比 (Carl Gustav Jacob Jacobi, 1804-1851)、凱萊 (Arthur Cayley, 1821-1895)、西爾維斯特 (James Joseph Sylvester, 1814-1897)……等等，都對20世紀之前的行列式發展，做出了不可抹滅的貢獻。

從歷史的發展，我們很清楚地看到，西方的行列式發展是從一次方程組求解開始的，數學家們發現用係數來表示方程組的解時，是有規律可循的。為了表示這規律，數學家們提出了不同的方式。 Continue reading →

西方行列式的發展：柯西的研究
（The Development of Determinants in West: Cauchy’s Work）
國立臺南第一高級中學林倉億老師

連結：西方行列式的發展：范德蒙的研究

雖然今日譯作「行列式」的詞 “determinantem”（即英文的“determinant”）是首次出現在高斯 (Carl Friedrich Gauss, 1777-1855) 於1801年出版的《算術研究》(Disquisitiones Arithmeticae) 中，但高斯是把它當作是字面意思來使用，即「決定的因素」，用以表示多元高次式的「判別式」，這和今日「行列式」的意義並不相同。

到了1812年，柯西 (Augustin-Louis Cauchy, 1789-1857) 在提交給法蘭西學院 (Institut de France) 的第二篇論文中（1815年出版），使用“déterminan”（即英文的“determinant”）來表示今日所稱的「行列式」，換言之，柯西才是使用「行列式」名詞的第一人。

在介紹柯西的行列式研究之前，我們必須先說明柯西在1812年之前的數學知識背景。首先，函數在19世紀是數學研究的熱門主題，柯西也是熱衷於各式函數的研究，他後來還對何謂函數下了定義，該定義已經十分接近今日函數的定義。其次，柯西十分熟悉范德蒙 (Alexandre-Theophile Vandermonde, 1735-1796)在行列式方面的研究（范德蒙並沒有使用行列式這名稱），在他1812年的論文中，多次提到了范德蒙的研究。然而，范德蒙的論文只是在呈現一種新的符號及其操作（參閱本網站〈西方行列式的發展：范德蒙的研究〉一文），並沒有函數的內涵。所以，柯西所做的，就是從函數的觀點來定義行列式。 Continue reading →

西方行列式的發展：范德蒙的研究
（The Development of Determinants in West: Vandermonde’s Work）
國立臺南第一高級中學林倉億老師

連結：西方行列式的發展：范德蒙的生平(2)

范德蒙1772年提交法國科學院的論文〈關於消去法的報告〉(Mémoire sur l’Élimination)是數學家首度將行列式運算作為研究主題的論文。范德蒙一開始就對他的符號給出了定義 （見圖一）：

\(\left. {\frac{{\,\alpha \,}}{{\,a\,}}} \right|\frac{{\,\beta \,}}{{\,b\,}} = \begin{array}{*{20}{c}} \alpha \\ a \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\begin{array}{*{20}{c}} \beta \\ b \end{array}\; – \;\begin{array}{*{20}{c}} \alpha \\ b \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\begin{array}{*{20}{c}} \beta \\ a \end{array}\)

\(\left. {\left. {\frac{{\,\alpha \,}}{{\,a\,}}} \right|\frac{{\,\beta \,}}{{\,b\,}}} \right|\frac{{\,\gamma \,}}{{\,c\,}} = \begin{array}{*{20}{c}} \alpha \\ a \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,\beta \,}}{{\,b\,}}} \right|\frac{{\,\gamma \,}}{{\,c\,}}\; + \;\begin{array}{*{20}{c}} \alpha \\ b \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\left. {\frac{{\,\beta \,}}{{\,c\,}}} \right|\frac{{\,\gamma \,}}{{\,a\,}}\; + \;\begin{array}{*{20}{c}} \alpha \\ c \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\frac{{\,\beta \,}}{{\,a\,}}} \right|\frac{{\,\gamma \,}}{{\,b\,}}\)

\(\begin{array}{ll} \left. {\left. {\frac{{\,\alpha \,}}{{\,a\,}}} \right|\frac{{\,\beta \,}}{{\,b\,}}} \right|\left. {\frac{{\,\gamma \,}}{{\,c\,}}} \right|\frac{{\,\delta \,}}{{\,d\,}} &= \begin{array}{*{20}{c}} \alpha \\ a \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\left. {\frac{{\,\beta \,}}{{\,b\,}}} \right|\frac{{\,\gamma \,}}{{\,c\,}}} \right|\frac{{\,\delta \,}}{{\,d\,}}\; – \;\begin{array}{*{20}{c}} \alpha \\ b \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\left. {\left. {\frac{{\,\beta \,}}{{\,c\,}}} \right|\frac{{\,\gamma \,}}{{\,d\,}}} \right|\frac{{\,\delta \,}}{{\,a\,}}\; \\&+\;\begin{array}{*{20}{c}} \alpha \\ c \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\left. {\left. {\frac{{\,\beta \,}}{{\,d\,}}} \right|\frac{{\,\gamma \,}}{{\,a\,}}} \right|\frac{{\,\delta \,}}{{\,b\,}}\; – \;\begin{array}{*{20}{c}} \alpha \\ d \end{array}\;\begin{array}{*{20}{c}} {}\\ . \end{array}\;\left. {\left. {\frac{{\,\beta \,}}{{\,a\,}}} \right|\frac{{\,\gamma \,}}{{\,b\,}}} \right|\frac{{\,\delta \,}}{{\,c\,}}\\ \;\;\;\; \vdots \\ \;\;\;\; \vdots \end{array}\) Continue reading →