Dandelin Spheres證明圓錐截痕的焦點性質
臺北市立西松高中數學科蘇惠玉老師

目前實施的99課綱高中數學中，弱化了圓錐曲線的單元，所謂的「圓錐截痕」不再是必須教授的單元。各版本課本或數學教師在教授時也僅是簡單的陳述平面與圓錐的截痕何時為圓、橢圓、拋物線或雙曲線，基本上與課本採用的焦點定義方式無法連結，學生只是被動地接受老師所說的與模型所看到的曲線名稱而已。

不過，藉由 Dandelin 球面的想法，我們可將圓錐截痕與焦點的定義方式連結，以一種較為簡潔的形式，證明阿波羅尼斯在《錐線論》中所陳述與證明的性質。 Continue reading →

求一術與插值多項式
臺北市立西松高中數學科蘇惠玉老師

一、求一術

所謂求一術，即是一般所稱的中國剩餘定理，指的是解一次同餘式的問題，例如：

今有物不知其數，三三數之賸二，五五數之賸三，七七數之賸二，問物幾何？

這樣的問題首先出現在《孫子算經》一書中。一般這個問題就稱為「孫子問題」，這種問題在民間流傳頗廣，通常有「秦王暗點兵」、「韓信點兵」、「翦管術」、「鬼谷算」等稱法。

孫子問題即是「求一數 \(N\)，除以 \(3\) 餘 \(2\)，除以 \(5\) 餘 \(3\)，除以 \(7\) 餘 \(2\)」，這個問題不僅是一個提昇讀者興趣的題目，它和古代曆法的推算有密切的關係。我們用 \(N\equiv r_i(\bmod~m_i)\) 符號代表 \(N\) 用 \(m_i\) 去除餘 \(r_i\)，例如 \(N\equiv 2(\bmod~3)\) 表示一數 \(N\) 除以 \(3\) 餘 \(2\)，因此這類問題即是解下列的聯利一次同餘式： Continue reading →

三次方程式的根式解
臺北市立西松高中數學科蘇惠玉老師

1545 年，義大利的一位醫生兼數學家卡丹諾(Gerolamo Cardano, 1501-1576)出版了《大技術Ars Magna or The Rules of Algebra》，首次向世人展示了如何求解三次與四次方程式的完整過程。然而三次方程式的根式解，如同許多數學上的偉大成就一般，無法只歸功於卡丹諾一人，甚至在其公開的過程中，為了優先權之爭，還引起公開挑戰、言語攻訐、陰謀策劃等等，算是數學史發展上相當具有社會史色彩的一頁。 Continue reading →

算幾不等式的證明(III)(Inequality of arithmetic and geometric means)
國立蘭陽女中數學科陳敏晧老師

已知：\(a_1,a_2,…,a_n\) 為正數或零。

求證：

\(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n} \ge \sqrt[n]{{{a_1}{a_2}…{a_n}}}\)，“\(=\)” 成立時若且唯若，\(a_1=a_2=…=a_n\)。

(其中 \(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n}\) 稱為算術平均數AM，\(\sqrt[n]{a_1a_2…a_n}\) 稱為幾何平均數GM)。

在此篇文章中，筆者再介紹兩種證明算幾不等式的方法，第一個稱為「調整法」，第二個是波里亞(George Pólya,1887 –1985) 的指數證明方法。

Continue reading →

算幾不等式的證明(II)(Inequality of arithmetic and geometric means)
國立蘭陽女中數學科陳敏晧老師

連結：算幾不等式的證明(I)

已知：\(a_1,a_2,…,a_n\) 為正數或零。

求證：

\(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n} \ge \sqrt[n]{{{a_1}{a_2}…{a_n}}}\)，“\(=\)” 成立時若且唯若，\(a_1=a_2=…=a_n\)。

(其中 \(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n}\) 稱為算術平均數，\(\sqrt[n]{{{a_1}{a_2}…{a_n}}}\) 稱為幾何平均數)。

除了常見的倒回的證明外(先證 \(n=2=2^1\) 再推論 \(n=4=2^2\)，然後反推 \(n=3\)，接著證明 \(n=8=2^3\)，然後反推 \(n=5,6,7\) 等)，在此處筆者再介紹兩種直接證明方法。

Continue reading →

算幾不等式的證明(I)(Inequality of arithmetic and geometric means)
國立蘭陽女中數學科陳敏晧老師

若 \(a,b\) 為正數或零，則 \(\displaystyle\frac{{a + b}}{2} \ge \sqrt {ab}\)，“\(=\)” 成立時若且唯若，\(a=b\)。

(其中 \(\displaystyle\frac{{a + b}}{2}\) 稱為 \(a,b\) 的算術平均數，\(\sqrt{ab}\) 稱為 \(a,b\) 的幾何平均數)

代數證明：

\(\displaystyle\frac{{a + b}}{2}-\sqrt {ab}= \frac{1}{2}(a + b – 2\sqrt {ab} ) = \frac{1}{2}{\left({\sqrt a-\sqrt b } \right)^2}\ge 0\)，

因此，\(\displaystyle\frac{{a + b}}{2} \ge \sqrt {ab}\)，“\(=\)” 成立時，\(\displaystyle\frac{1}{2}{(\sqrt a-\sqrt b)^2} = 0\)，

所以，\(a=b\)，反之亦然。

算幾不等式可以推廣至 \(n\) 的情形，也就是若 \(a_1,a_2,…,a_n\) 為正數或零，

則 \(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n} \ge \sqrt[n]{{{a_1}{a_2}…{a_n}}}\)，“\(=\)” 成立時若且唯若，\(a_1=a_2=…=a_n\)。

(其中 \(\displaystyle\frac{{{a_1} + {a_2} + … + {a_n}}}{n}\) 稱為 \(a_1,a_2,…,a_n\) 的算術平均數，\(\sqrt[n]{{{a_1}{a_2}…{a_n}}}\) 稱為 \(a_1,a_2,…,a_n\) 的幾何平均數) Continue reading →

賭金分配問題 (The Problem of Division of the Stakes)(二)
國立屏東高級中學數學科楊瓊茹老師

參考 賭金分配問題(一)

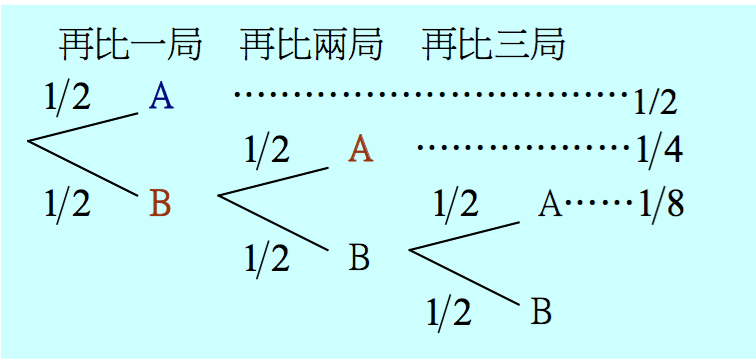
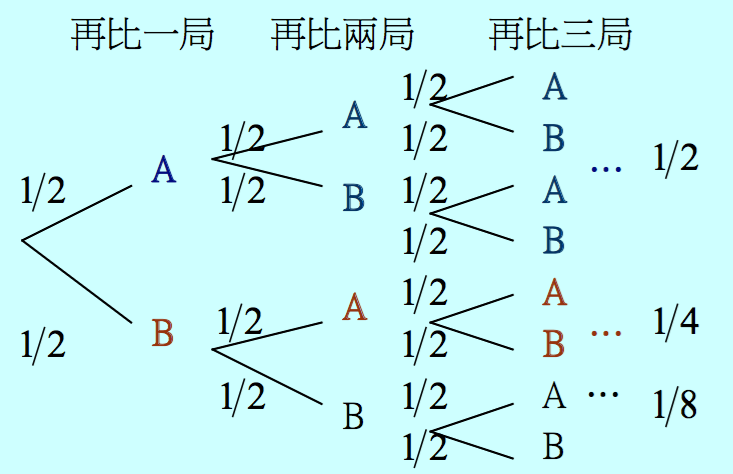
在費馬的解法中，他考慮再比賽三局所有可能的情況為(\(A\)表甲勝、\(B\)表乙勝)：

不過，還要比 \(3\) 局的計算方式似乎有些奇怪，因為在甲已勝 \(5\) 局的優勢下，AAA這三場中根本就不必再比最後兩局、BAB中也不用比最後一局。事實上，我們在甲得 \(6\) 勝時比賽就結束，這兩個想法乍看之下顯然有些不同，但其實是相同的。因為不管甲 \(6\) 勝時是否還打了後面那幾局，那些結果“依然存在”(參見樹狀圖)。

Continue reading →

賭金分配問題 (The Problem of Division of the Stakes)(一)
國立屏東高級中學數學科楊瓊茹老師

機率史上，賭金分配問題曾引起許多數學家們的討論，筆者將這些內容和數據略作調整，使得能夠用一道題目為例，分別呈現出數學家–帕西歐里、塔爾塔利亞、費馬和巴斯卡–對於賭金分配的看法：

假設甲乙兩人進行一場公平的比賽，且甲乙兩人實力相當，各出資 \(12\) 枚金幣作為賭注，必須要贏 \(6\) 局才能贏得賭金，目前甲以 \(5:3\) 領先。在此假設下，若比賽因故終止，則此時應如何分配賭金？

帕西歐里 ( Luca Pacioli, 1445-1509 ) 的解法根據已贏得的局數比例作分配，甲得 \({\rm{24}} \times \frac{{\rm{5}}}{{\rm{8}}} = {\rm{15}}\) 枚金幣、乙得 \({\rm{24}} \times \frac{{\rm{3}}}{{\rm{8}}} = {\rm{9}}\) 枚金幣。

塔爾塔利亞 ( Niccolò Tartaglia, 1499-1557 ) 注意到帕西歐里的答案是錯誤的，因為若假設局數比為 \(1:0\)，則甲拿走所有的賭金，這顯然毫無道理。他認為甲乙兩人相差 \(2\) 局，這 \(2\) 局的差距是總局數 \(6\) 局的三分之一，甲應拿走乙方賭金的三分之一，也就是甲得 \({\rm{12}} + \frac{{{\rm{(5 – 3)}}}}{{\rm{6}}} \times {\rm{12}} = {\rm{16}}\) 枚金幣，乙得 \({\rm{12 – }}\frac{{{\rm{(5 – 3)}}}}{{\rm{6}}} = {\rm{8}}\) 枚金幣。 Continue reading →