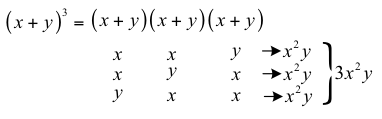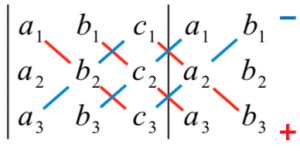西方行列式的發展：范德蒙的生平(2)
（The Development of Determinants in West: Vandermonde’s Biography (2)）
國立臺南第一高級中學林倉億老師

連結：西方行列式的發展：范德蒙的生平(1)

1772年范德蒙提交的第四篇論文，研究主題就是今日的行列式。范德蒙在這篇論文中，將行列式獨立成為一個數學研究對象（object），定義並推導相關性質後，再應用到一次方程組的解，也就是今日所謂的「克拉瑪公式」。在前人如萊布尼茲 (Gottfried Wilhelm Leibniz, 1646-1716)、克拉瑪 (Gabriel Cramer, 1704-1752)、貝祖 (Étienne Bézout, 1730-1783)等人的研究中都可發現今日行列式的運算，但那些運算都是依附在解方程組的過程之中，換言之，那些運算並沒有獨立成為數學的研究對象，被研究的主角是解方程組，而非這些運算。范德蒙正是因為這篇論文，才被推崇為行列式的創立者。那麼，究竟范德蒙在這篇論文之中是如何研究行列式的呢？這留待下一篇文章再作介紹。

范德蒙的研究並不侷限在數學之中，音樂和科學也有他的研究成果。例如1776年法國發生了一場嚴重的霜害，范德蒙就和數學家貝祖、化學家拉瓦錫 (Antoine-Laurent de Lavoisier, 1743-1794)作了一系列低溫的實驗，探討霜害產生的影響，並在1777年發表他們的研究結果。 Continue reading →

西方行列式的發展：范德蒙的生平(1)
（The Development of Determinants in West: Vandermonde’s Biography (1)）
國立臺南第一高級中學林倉億老師

連結：西方行列式的發展：貝祖的研究

范德蒙 (Alexandre-Theophile Vandermonde) 1735年生於巴黎；巴黎，也是他在1796年告別人世之地。范德蒙的生日與忌日，很巧合地，都是台灣的國定假日，分別是2月28日與1月1日，因此，當我們在台灣放假時，除了原有的紀念意義外，也不妨遙想這位數學家的貢獻，讓放假增添一點數學風味。

范德蒙的父親是一位醫生，擁有不錯的社會地位與經濟收入。但子承衣缽卻不是這位父親的選擇，自范德蒙年幼時，他就希望也鼓勵范德蒙成為一位音樂家。在父親的鼓舞下，數學並不是范德蒙年輕時感興趣的對象，小提琴才是。

直到35歲那年，受到數學家貝爾丹 (Alexis Fontaine des Bertins, 1704-1771)的熱情感召，才激起范德蒙對數學研究的興趣。當年，他就以非會員的身份在法國科學院宣讀一篇數學論文，這可說是一份殊榮。或許是貝爾丹的感召與科學院的光環，激發了范德蒙的研究潛能，他在短短兩年內就提交了四篇論文給科學院，奠定了他在數學史中的地位。1771年，范德蒙就被正式選為科學院的一員。35歲之前對數學沒什麼貢獻的音樂家，竟在36歲成了國家科學院的會員，這恐怕是空前絕後的紀錄了！范德蒙在提交給科學院的四篇論文中，第一篇 (1771)提出了方程式之根的 \(m\) 次和公式，並證明了當 \(n\) 是小於 \(10\) 的質數時，\(x^n-1=0\) 的解可用根式表達。第二篇 (1771)則是討論棋盤上騎士漫遊的問題，這主題看起來沒什麼實際應用，比較像是趣味數學，但其內在數學結構卻是和今日的拓樸學有關。第三篇 (1772)的內容與今日的高中數學有頗多的連結，值得我們進一步了解。

Continue reading →

從二項式定理到多項式定理 (2)（From Binomial Theorem to Multinomial Theorem (2)）
臺北市立第一女子高級中學蘇俊鴻老師

連結：從二項式定理到多項式定理(1)

在〈從二項式定理到多項式定理(1)〉中提到 \((x+y)^3\) 的 \(x^2y^1\) 項是如何產生呢？由於 \({\left( {x + y} \right)^3} = \left( {x + y} \right)\left( {x + y} \right)\left( {x + y} \right)\)，故可看成在三個 \((x+y)\) 括號中，二個選 \(x\) 一個選 \(y\) 相乘而得，如此選取的方法數為 \(C_1^3\)，所以 \(x^2y^1\) 項的係數是 \(C_1^3=3\)。

不過，也可換個方式來看 \(x^2y^1\) 項的產生。如圖一所示，選取二個選 \(x\)、一個 \(y\) 後，其情形等同於 \(2\) 個 \(x\) 與 \(1\) 個 \(y\) 的不盡相異物直線排列。因此，\(2\) 個 \(x\)、\(1\) 個 \(y\) 的直線排列可產生 \(x^2y^1\) 項，這樣的排列方法數為 \(\frac{3!}{1!2!}=3=C_1^3\)，故 \(x^2y^1\) 項的係數是 \(C_1^3=3\)。

圖一\(~~~(x+y)^3\) 部分集項示意圖

Continue reading →

從二項式定理到多項式定理 (1)（From Binomial Theorem to Multinomial Theorem (1)）
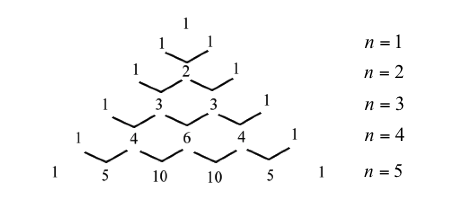
臺北市立第一女子高級中學蘇俊鴻老師

國中時學到乘法公式 \({(x + y)^2} = {x^2} + 2xy + {y^2}\)，\({(x + y)^3} = {x^3} + 3{x^2}y + 3x{y^2} + {y^3}\)，就在猜想 \({(x + y)^4},{(x + y)^5},\cdots,{(x + y)^n}\) 展開後的模樣。透過比對可看出 \((x+y)^n\) 的各項都是齊次，也就是說，展開的各項 \(x^ay^b\) 都會滿足 \(a+b=n\)。

因此，只要能掌握各項係數的規則，任意的自然數 \(n\)，我們便能將 \((x+y)^n\) 的各項依 \(x\) 或 \(y\) 的升冪或降冪排出。國中老師採用的方法是將巴斯卡三角形畫出(圖一)，一一對應，只要足夠耐心，就能達到任意的自然數 \(n\)。

圖一\(~~~\)巴斯卡三角形

Continue reading →

行列式的應用（Applications of Determinant）
國立臺南第一高級中學林倉億老師

連結：行列式的性質

以下介紹行列式在高中數學中主要的應用：

1. 表示平面上三角形的面積
   \(\vec{OA}=(a_1,b_1)\)、\(\vec{OB}=(a_2,b_2)\)，則 \(\Delta OAB\) 面積 \(= \frac{1}{2}\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|} \right|\)
   （\(\frac{1}{2}\) 乘以 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|\) 的絕對值）。
   【證明】：
   由三角形面積公式 \(\Delta OAB = \frac{1}{2}\sqrt {{{\left| {\vec{OA}} \right|}^2}{{\left| {\vec{OB}} \right|}^2} – {{\left( {\vec{OA} \cdot\vec{OB}} \right)}^2}}\)
   可得
   \(\begin{array}{ll}\Delta OAB &= \frac{1}{2}\sqrt {({a_{ 1}}^2 + {b_{ 1}}^2)({a_{ 2}}^2 + {b_{ 2}}^2) – {{\left( {{a_{ 1}}{a_{ 2}} + {b_{ 1}}{b_{ 2}}} \right)}^2}} \\&= \frac{1}{2}\sqrt {{a_{ 1}}^2{b_{ 2}}^2 + {a_{ 2}}^2{b_{ 1}}^2 – 2{a_{ 1}}{a_{ 2}}{b_{ 1}}{b_{ 2}}} = \frac{1}{2}\sqrt {{{\left( {{a_{ 1}}{b_{ 2}} – {a_{ 2}}{b_{ 1}}} \right)}^2}} \\&= \frac{1}{2}\sqrt { {{\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|}^2}} = \frac{1}{2}\left| {\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right|} \right|\end{array}\)
2. 表示空間中兩不平行向量的外積
   \(\vec{OA}=(a_1,b_1,c_1)\)，\(\vec{OB}=(a_2,b_2,c_2)\)，則 \(\vec{OA}\) 與 \(\vec{OB}\) 的外積
   可記作 \(\vec{OA}\times\vec{OB}= ( \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{c_{ 1}}}&{{a_{ 1}}}\\ {{c_{ 2}}}&{{a_{ 2}}} \end{array} } \right| , \left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| )\)  Continue reading →
3. 行列式的性質 2014/09/16

   行列式的性質（Properties of Determinant）
   國立臺南第一高級中學林倉億老師

   連結：行列式的定義

   在本文中，二階行列式的定義是 \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}} \end{array} } \right| = {a_{ 1}}{b_{ 2}} – {a_{ 2}}{b_{ 1}}\)，

   三階行列式的定義則是

   \(\left| { \begin{array}{*{20}{c}} {{a_{ 1}}}&{{b_{ 1}}}&{{c_{ 1}}}\\ {{a_{ 2}}}&{{b_{ 2}}}&{{c_{ 2}}}\\ {{a_{ 3}}}&{{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| = {a_{ 1}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 2}}}&{{c_{ 2}}}\\ {{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| – {a_{ 2}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 3}}}&{{c_{ 3}}} \end{array} } \right| + {a_{ 3}} \cdot \left| { \begin{array}{*{20}{c}} {{b_{ 1}}}&{{c_{ 1}}}\\ {{b_{ 2}}}&{{c_{ 2}}} \end{array} } \right| = {a_{ 1}}{b_{ 2}}{c_{ 3}} – {a_{ 1}}{b_{ 3}}{c_{ 2}} + {a_{ 2}}{b_{ 3}}{c_{ 1}} – {a_{ 2}}{b_{ 1}}{c_{ 3}} + {a_{ 3}}{b_{ 1}}{c_{ 2}} – {a_{ 3}}{b_{ 2}}{c_{ 1}}\) 

   我們稱直的為行，由左而右依序是第1行、第2行、…；稱橫的為列，由上而下依序是第1列、第2列、…。利用定義，很容易可以推出下列二階與三階行列式性質，證明就略去。 Continue reading →

4. 行列式的定義 2014/09/16

   行列式的定義 (Definitions of Determinant)
   國立臺南第一高級中學林倉億老師

   在高中數學課本中，對於二階與三階行列式，基本上都是直接給出操作型定義：

   定義1：\(\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{b_{1}}}\\ {{a_{2}}}&{{b_{2}}} \end{array}} \right| = {a_{1}}{b_{2}} – {a_{2}}{b_{1}}\)。

   等號的左邊稱為二階行列式，等號的右邊稱為二階行列式的展開式，或稱為二階行列式的值。

   定義2：\(\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{b_{1}}}&{{c_{1}}}\\ {{a_{2}}}&{{b_{2}}}&{{c_{2}}}\\ {{a_{3}}}&{{b_{3}}}&{{c_{3}}} \end{array}} \right| = {a_{1}}{b_{2}}{c_{3}} + {a_{2}}{b_{3}}{c_{1}} + {a_{3}}{b_{1}}{c_{2}} – {a_{3}}{b_{2}}{c_{1}} – {a_{2}}{b_{1}}{c_{3}} – {a_{1}}{b_{3}}{c_{2}}\)

   等號的左邊稱為三階行列式，等號的右邊稱為三階行列式的展開式，或稱為三階行列式的值。

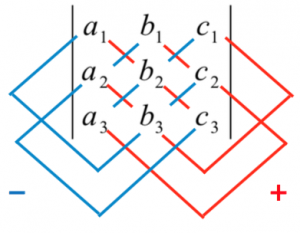
   然後再根據定義推導相關的運算性質，最後再介紹它們的應用。定義二其實很難記憶，因此一般教科書都會補充記憶的方法，就是將圖一或圖二中，紅線上的數乘積之和，減去藍線上的數乘積之和。

   

   圖一

   

   圖二

   Continue reading →

5. 等差數列 (Arithmetic Progression) 2014/09/15

   等差數列 (Arithmetic Progression)
   國立蘭陽女中陳敏晧教師

   一連串有次序的數，稱為數列(sequence)。其中的數，稱為項(term)；第一個項，稱為首項，以 \(a_1\) 表示；第 \(n\) 個項以 \(a_n\)表示。若數列中每一個後項減去前項的值固定時，則稱此數列為等差數列(Arithmetic Progression，簡寫為AP)，我們將此固定差值稱為公差(common difference)，以 \(d\) 表示。

   因為 \(a_2-a_1=d\)，所以 \(a_2=a_1+d\)。又 \(a_3-a_2=d\)，所以 \(a_3=a_2+d=a_1+2d\)。我們很容易推得 \(a_n=a_1+(n-1)d,~n\in \mathbb{N}\)。進一步可得 \({a_n} = {a_m} + (n – m)d\)，其中 \(n,m\in \mathbb{N}\)。

   Continue reading →