- 正弦定律 (The Sine Law) 2013/10/11
正弦定律 (The Sine Law)
臺北市立第一女子中學數學科蘇俊鴻老師在現行高中課程中,對於正弦定律的推導常是透過三角形面積公式為媒介:
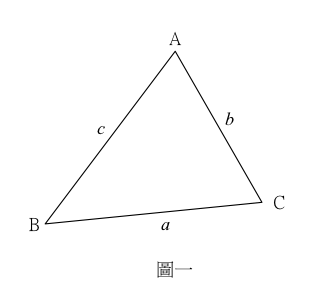
如圖一,給定三角形 \(\Delta ABC\) ,則三角形 \(\Delta ABC\) 的面積為
\(\displaystyle\frac{1}{2}ab\sin C = \frac{1}{2}ac\sin B = \frac{1}{2}bc\sin A\)
因此,\(\displaystyle\frac{{\sin C}}{c} = \frac{{\sin B}}{b} = \frac{{\sin A}}{a} \Rightarrow \frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)
- 輾轉相除法(IV) (Euclidean algorithm) 2013/10/07
輾轉相除法(IV) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師連結:輾轉相除法(III)
一、五猴分桃問題:
五隻猴子分一堆桃子,怎麼分也不能均分成五份,大家約定先去睡覺,明天再說。夜裡,猴甲偷偷起來,吃掉一個,這時發現其餘正好可以分成五份,結果猴甲把自己那份藏起來,又躺去睡覺了;接著猴乙也偷偷起來,吃掉一個,發現其餘也正好可以分成五份,結果猴乙也把自己那份藏起來;猴丙,猴丁,都如法炮製。而猴戊吃掉一個後,也發現餘桃數為 $$5$$ 的倍數。問總桃數最少有幾個?
參考解法:
假設總桃數為 $$x$$,而 $$y$$ 為某個正整數。
因為 $$\displaystyle\frac{1}{5}\left[ {\frac{4}{5}\left[ {\frac{4}{5}\left[ {\frac{4}{5}\left[ {\frac{4}{5}\left( {x – 1} \right) – 1} \right] – 1} \right] – 1} \right] – 1} \right] = y$$
整理方程式得:$$256x-3125y=2101$$ (此即為不定方程式),
利用歐幾里得的想法,我們先考慮 $$256x+3125y=1$$
$$\begin{array}{rl} 3125 &=12 \times 256+53\\256&=4\times 53+44\\53&=1\times 44+9\\44&=4\times 9+8\\9&=1\times 8+1\end{array}$$
- 輾轉相除法(III) (Euclidean algorithm) 2013/10/07
輾轉相除法(III) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師連結:輾轉相除法(II)
一、輾轉相除法與連分數
首先讓我們來練習一下輾轉相除法,求 $$(42897, 18644)=\underline{~~~~~~~~~~~~~~~}$$。
(1)橫式過程:$$42897=2\times 18644+5609$$
$$18644=3\times 5609+1817$$
$$5609=3\times 1817+158$$
$$1817=11\times 158+79$$
$$158=2\times 79+0$$$$\therefore \left( {42897,18644} \right) = \left( {18644,5609} \right) = \left( {5609,1817} \right) = \left( {1817,158} \right) = \left( {158,79} \right) = \left( {79,0} \right) = 79$$
Continue reading →
- 輾轉相除法(II) (Euclidean algorithm) 2013/10/07
輾轉相除法(II) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師連結:輾轉相除法(I)
一、畢氏音律與輾轉相減法
 西元前五百多年,畢達哥拉斯(Pythagoras of Samos, c. 570 BC – c. 495 BC)(如右圖)為了探求音律,利用單弦琴(monochord)作實驗,發現兩個音的弦長為簡單整數比時,是和諧悅耳的。例如:$$2:1$$,$$3:2$$,$$4:3$$,$$5:4$$ 分別是八度、五度、四度及三度音程。這些弦長的比是如何求得的呢?若是分成 $$3:2$$,則會產生悅耳的和弦音樂,因此,不同的弦長比例會導致不同的音高,若是比例不正確,則會形成不和諧的和弦聲。
西元前五百多年,畢達哥拉斯(Pythagoras of Samos, c. 570 BC – c. 495 BC)(如右圖)為了探求音律,利用單弦琴(monochord)作實驗,發現兩個音的弦長為簡單整數比時,是和諧悅耳的。例如:$$2:1$$,$$3:2$$,$$4:3$$,$$5:4$$ 分別是八度、五度、四度及三度音程。這些弦長的比是如何求得的呢?若是分成 $$3:2$$,則會產生悅耳的和弦音樂,因此,不同的弦長比例會導致不同的音高,若是比例不正確,則會形成不和諧的和弦聲。原來畢達哥拉斯是利用逐步相減法(the successive subtraction)求得的:考慮 $$a$$、$$b$$ 兩弦,不妨設 $$a>b$$,從 $$a$$ 減去較小的 $$b$$,得 $$a-b$$;若 $$a-b$$ 仍大於 $$b$$,再減去 $$b$$ 得 $$a-2b$$;…,直到 $$a-tb\le b$$,其中 $$t\in\mathbb{N}$$。繼續從較大的 $$b$$ 減去較小的 $$a-tb$$,…,直到 $$b-l(a-tb)\le a-tb$$,其中$$l\in\mathbb{N}$$。按此要領反覆做下去,經過有限步的輾轉相減後,必可得到 $$0$$,此時運算停止。在 $$0$$ 之前最後一個不為 $$0$$ 的數 $$d$$,即最大公因數 $$d$$。
畢達哥拉斯相信,任意給定兩正整數 $$a$$、$$b$$,必可利用有限次的逐步相減運算,找到最後一個不為 $$0$$ 的正整數 $$d$$,所以,存在正整數 $$p$$、$$q$$,使得 $$a=pd~, b=qd$$,而 $$d$$ 為滿足此式的最大弦長,從而得到 $$a:b =p:q$$ 為整數比,我們稱這種演算法稱為輾轉相減法。 Continue reading →
- 實數的三角不等式 2013/10/06
實數的三角不等式 (Triangle Inequality for Real Numbers)
國立蘭陽女中數學科陳敏晧老師若 \(a,b\) 為實數,\(\left| a \right| + \left| b \right| \ge \left| {a + b} \right|\),“\(=\)”成立時,\(ab\ge 0\)。(此不等式可以利用三角形的兩邊之和大於第三邊來理解,因此,稱之為三角不等式。)
證明:
因為 \(\left| a \right| + \left| b \right| \ge 0,~\left| {a + b} \right| \ge 0\),直接相減或相除無法順利運算,因此,考慮平方相減
\(\begin{array}{ll}{\left( {\left| a \right| + \left| b \right|} \right)^2} – {\left| {a + b} \right|^2} &= \left( {{{\left| a \right|}^2} + 2\left| a \right|\left| b \right| + {{\left| b \right|}^2}} \right) – {\left( {a + b} \right)^2}\\&= \left( {{a^2} + 2\left| {ab} \right| + {b^2}} \right) – ({a^2} + 2ab + {b^2})\\&= 2\left( {\left| {ab} \right| – ab} \right) \ge 0\end{array}\)
因此,\({\left( {\left| a \right| + \left| b \right|} \right)^2} \ge {\left| {a + b} \right|^2}\),即 \(\left| a \right| + \left| b \right| \ge \left| {a + b} \right|\)
“\(=\)”成立時, 即 \(\left| {ab} \right| – ab = 0\)移項得 \(\left| {ab} \right| = ab\),\(\therefore ab\ge 0\)。
- 畢氏定理(Pythagoras Theorem) 2013/10/06
畢氏定理(Pythagoras Theorem)
國立蘭陽女中數學科陳敏晧老師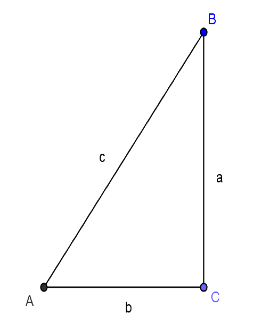 已知:直角三角形 $$ABC$$,其中 $$\angle BAC=90^\circ$$,
已知:直角三角形 $$ABC$$,其中 $$\angle BAC=90^\circ$$,而 $$\overline{AB}=c$$,$$\overline{BC}=a$$,$$\overline{CA}=b$$。
求證 $$a^2+b^2=c^2$$。
證明:
方法一:《幾何原本》作法
由直角 $$C$$ 往斜邊 $$\overline{AB}$$ 作直線,交 $$\overline{AB}$$ 邊於 $$K$$ 點,交 $$\overline{GF}$$ 邊於 $$J$$ 點。只要證明正方形 $$ACDE$$ 的面積等於長方形 $$AKJG$$ 的面積;正方形 $$BCHI$$ 的面積等於長方形 $$BKJF$$ 的面積,便完成畢氏定理的證明。 Continue reading →
- 輾轉相除法(I) (Euclidean algorithm) 2013/10/06
輾轉相除法(I) (Euclidean algorithm)
國立蘭陽女中數學科陳敏晧老師歷史溯源:歐幾里得(Euclid,ca.325BC-ca.265BC)(如右圖)的《幾何原本(Elements)》第七卷的第一、二個命題論述如何用輾轉相除法求兩整數的最大公因數,因此,輾轉相除法又稱歐幾里得算法。
狄里克利(Peter Gustav Lejeune Dirichlet, 1805-1859)在他的《數論》一書中說「本書的整個結構奠定在一塊基石上面,即計算兩個整數的最大公因數(輾轉相除法)。」利用這個方法,可以較快地求出兩個自然數的最大公因數,稱為 g.c.d.(greatest common divisior)[1]。 所謂最大公因數,是指幾個數的共有的因數之中最大的一個,例如:8和12的最大公因數是4,記作 g.c.d.(8,12)=4。 Continue reading →
- 矩陣的運算(Operations of Matrices) 2013/10/06
矩陣的運算(Operations of Matrices)
國立臺南第一高級中學數學科林倉億老師摘要:本文介紹矩陣的加法、減法、係數積,以及如何操作矩陣的乘法。
矩陣的加法與減法
當兩個矩陣的列數相等,行數也相等時,我們就稱它們為「同階矩陣」。
例如 $$M = \left[ \begin{array}{l} \begin{array}{*{20}{c}} 1&2&3 \end{array}\\ \begin{array}{*{20}{c}} 4&5&6 \end{array} \end{array} \right]$$ 與 $$N = \left[ \begin{array}{l} \begin{array}{*{20}{c}} {1{\rm{0}}}&{2{\rm{0}}}&{3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {4{\rm{0}}}&{5{\rm{0}}}&{6{\rm{0}}} \end{array} \end{array} \right]$$ 同為 $$2\times 3$$ 階矩陣。
同階矩陣我們才能做加法與減法,方法很直觀,就是相同位置的元相加或相減,例如:
$$\begin{array}{ll}M + N &= \left[ \begin{array}{l} \begin{array}{*{20}{c}} 1&2&3 \end{array}\\ \begin{array}{*{20}{c}} 4&5&6 \end{array} \end{array} \right] + \left[ \begin{array}{l} \begin{array}{*{20}{c}} {1{\rm{0}}}&{2{\rm{0}}}&{3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {4{\rm{0}}}&{5{\rm{0}}}&{6{\rm{0}}} \end{array} \end{array} \right]{\rm{ = }}\left[ \begin{array}{l} \begin{array}{*{20}{c}} {{\rm{1 + }}1{\rm{0}}}&{{\rm{2 + }}2{\rm{0}}}&{{\rm{3 + }}3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {{\rm{4 + }}4{\rm{0}}}&{{\rm{5 + }}5{\rm{0}}}&{{\rm{6 + }}6{\rm{0}}} \end{array} \end{array} \right]\\&= \left[ \begin{array}{l} \begin{array}{*{20}{c}} {1{\rm{1}}}&{2{\rm{2}}}&{3{\rm{3}}} \end{array}\\ \begin{array}{*{20}{c}} {4{\rm{4}}}&{5{\rm{5}}}&{6{\rm{6}}} \end{array} \end{array} \right]\end{array}$$
$$\begin{array}{ll}M – N &= \left[ \begin{array}{l} \begin{array}{*{20}{c}} 1&2&3 \end{array}\\ \begin{array}{*{20}{c}} 4&5&6 \end{array} \end{array} \right] – \left[ \begin{array}{l} \begin{array}{*{20}{c}} {1{\rm{0}}}&{2{\rm{0}}}&{3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {4{\rm{0}}}&{5{\rm{0}}}&{6{\rm{0}}} \end{array} \end{array} \right]{\rm{ = }}\left[ \begin{array}{l} \begin{array}{*{20}{c}} {{\rm{1}} – 1{\rm{0}}}&{{\rm{2}} – 2{\rm{0}}}&{{\rm{3}} – 3{\rm{0}}} \end{array}\\ \begin{array}{*{20}{c}} {{\rm{4}} – 4{\rm{0}}}&{{\rm{5}} – 5{\rm{0}}}&{{\rm{6}} – 6{\rm{0}}} \end{array} \end{array} \right] \\&=\left[ \begin{array}{l} \begin{array}{*{20}{c}} {\; – \;{\rm{9}}}&{ – {\rm{18}}}&{ – {\rm{27}}} \end{array}\\ \begin{array}{*{20}{c}} { – {\rm{36}}}&{ – {\rm{4}}5}&{ – {\rm{54}}} \end{array} \end{array} \right]\end{array}$$
用符號來表示就是 $$A = {\left[ {{a_{ij}}} \right]_{m \times n}}$$,$$B = {\left[ {{b_{ij}}} \right]_{m \times n}}$$,
則 $$A+B = {\left[ a_{ij}+b_{ij} \right]_{m \times n}}$$,$$A-B = {\left[ a_{ij}-b_{ij} \right]_{m \times n}}$$。
- 輾轉相除法(IV) (Euclidean algorithm) 2013/10/07
Insert math as
Additional settings
Formula color
Type math using LaTeX
Preview
\({}\)
Nothing to preview
Insert