- 從複數到三角函數公式(I) (From complex number to trigonometric function formulas) 2014/09/07
從複數到三角函數公式(I) (From complex number to trigonometric function formulas)
國立蘭陽女中陳敏晧教師複數在數學各領域均有重大影響,本文章將討論如何以複數的形式來證明三角函數的相關公式,由於複數具有極坐標形式,可以將角度做旋轉、長度做伸縮變換,這是傳統幾何學在直角坐標平面難以突破的面向,因此,利用複數來證明三角函數公式往往會有意想不到的收穫,也常使學習者見識到數學之美!
本文將使用到歷史法國數學家棣美弗(Abraham de Moivre, 1667-1754)於1730年發表的棣莫弗公式,即若 \(z = r(\cos \theta+ i\sin \theta)\),則 \({z^n} = {r^n}(\cos n\theta+ i\sin n\theta ),n \in Z\)。
及歐拉(Leonhard Euler, 1707-1783)在1748年所發表的歐拉公式:\({e^{i\theta }} = \cos \theta+ i\sin \theta\)。
- 和算家求橢圓周長的方法(二)(Wasan’s method of finding the formula of the circumference of an ellipse Ⅱ) 2014/09/06
和算家求橢圓周長的方法(二)
(Wasan’s method of finding the formula of the circumference of an ellipse Ⅱ)
臺北市立和平高中教師黃俊瑋如前文〈和算家求橢圓周長的方法(一)〉所述,和田寧是最早造出正確橢圓周長展開式的數學家,然而,他的主要著作皆在西元1836年的一場大火中付之一炬,因此,我們只得以他授予的弟子們的傳書,一窺他求解橢圓周長的方法。
和田寧的弟子小出兼政,依據和田寧所授之傳書編成《圓理算經》,該書〈上卷〉的第五部份裡,提出了求橢圓周長問題:「譬今有如圖橢圓,只言長徑若干,短徑若干,問得周長術如何?」作者造橢圓周長公式的過程中,主要是利用分割求和的積分方式,輔以各類「圓理表」。以下,筆者進一步說明並分析他求橢圓周長的過程。
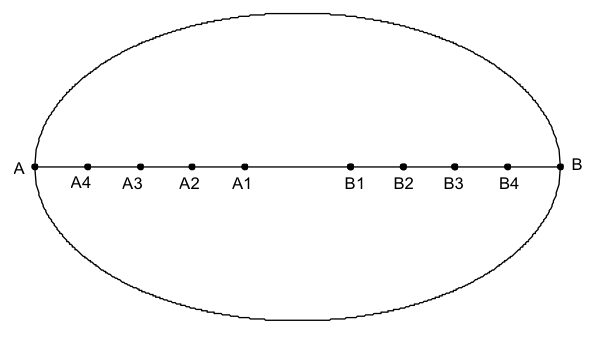
假設橢圓之長軸長為 \(2a\)、短軸長為 \(2b\),首先,小出兼政先利用「截弦順法對橢圓之長軸作分割,配對得到 \(n\) 段,讀者請參考圖一,以分割成配對 \(5\) 等分的情況為例作說明。此分割法是以左右配對 \(5\) 等分割的方式,對橢圓之長軸作分割,使其滿足:
\(\overline{{A_1}{B_1}}=\overline {{A_1}{A_2}}+\overline {{B_1}{B_2}}=\overline{{A_2}{A_3}}+\overline{{B_2}{B_3}}= \overline{{A_3}{A_4}}+\overline{{B_3}{B_4}}=\overline{{A_4}A}+\overline{{B_4}B}=\frac{{2a}}{5}\)
這和現代教科書中所用的等分割方式有所不同。
- 和算家求橢圓周長的方法(一)(Wasan’s method of finding the formula of the circumference of an ellipse Ⅰ) 2014/09/06
和算家求橢圓周長的方法(一)
(Wasan’s method of finding the formula of the circumference of an ellipse Ⅰ)
臺北市立和平高中教師黃俊瑋相較於圓周長與而言,橢圓周長是早期數學家們感到棘手的問題。一般而言,我們可以利用定積分法,求得橢圓的面積。
首先,不失一般性,我們可把橢圓的長軸固定在 \(x\) 軸的方向上,
則其標準方程式為:\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) (長軸半長為 \(a\),短軸半長為 \(b\))。
當我們考慮函數 \(y=\sqrt{b^2-\frac{b^2}{a^2}x^2}=\frac{b}{a}\sqrt{a^2-x^2}\) 時,可以利用定積分求得橢圓面積為第一象限部份面積的 \(4\) 倍(如圖一所示),即 \(ab\pi\)。特別地,當橢圓的長軸與短軸等長(亦即當 \(2a=2b\))時,可得圓面積公式 \(\pi a^2\)。- 平面上點到直線距離(三) 2014/09/02
平面上點到直線距離(三) (The distance from a point to a line in the plane Ⅲ)
臺北市立和平高中教師黃俊瑋連結:平面上點到直線距離(二)
本文承〈平面上點到直線距離(一)〉與〈平面上點到直線距離(二),繼續提出三類平面上點到直線距離的解法以及相關討論與連結。而本文中的各類解法,主要在直線上任取一點或兩點,造出新向量,所延伸出的方法。
方法5:在直線上任取一點,再利用平行與垂直性質
本類方法主要是引入直線上的一點後,充份利用直線的法向量與方向向量,輔以平行與垂直相關性質與關係,求得投影點與距離。
方法5-1:在直線上任取一點,再利用平行與垂直相關性質
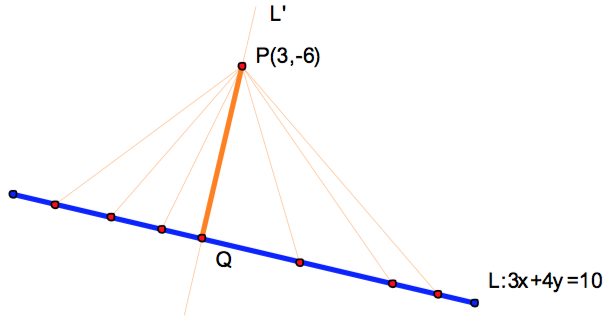
在 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\),則 \(\vec{P’P}=(1,-7)\) ,
令 \(Q\) 為 \(P(3,-6)\) 在 \(L\) 的投影點,\(\vec{P’Q}\) 與直線之方向向量平行,可設為 \(\vec{P’Q}=t(4,-3)\)。接下來,可發展出兩種方法,分別利用直線的法向量或方向向量,搭配平行與垂直關係進行解題:
5-1-1
則 \(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 平行直線 \(L:3x+4y=10\) 的法向量
分量成比例 \(\frac{{1 – 4t}}{{ – 7 + 3t}} = \frac{3}{4}\),可得 \(4(1-4t)=3(-7+3t)\),解之可得 \(t = 1\),
可得投影點為 \(Q(6,-2)\),則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。5-1-2
\(\vec{QP}=\vec{P’P}-\vec{P’Q}=(1-4t,-7+3t)\) 垂直直線 \(L:3x+4y=10\) 的方向向量
內積為 \(4(1 – 4t) + ( – 3)( – 7 + 3t) = 0\),解之可得 \(t = 1\),
可得投影點為 \(Q(6,-2)\),則 \(\overline{PQ}\) 之距離 \(5\) 即為所求(參考圖一所示)。Continue reading →
- 平面上點到直線距離(二) 2014/09/02
平面上點到直線距離(二) (The distance from a point to a line in the plane Ⅱ)
臺北市立和平高中教師黃俊瑋連結:平面上點到直線距離(一)
本文承〈平面上點到直線距離(一)〉,繼續提出三類平面上點到直線距離的解法以及相關討論與知識間的連結。
方法2:利用向量平行與垂直等關係
方法2-1:利用向量 \(PQ\) 與 \(L\) 之方向向量垂直。
利用直線 \(L:3x+4y=10\) 的參數式,
可假設 \(P(3,-6)\) 在 \(L\) 上的投影點 \(Q(2+4t,1-3t)\),
因為 \(\overline{PQ}\) 垂直直線 \(L\),所以 \(\overline{PQ}\) 為最短距離。
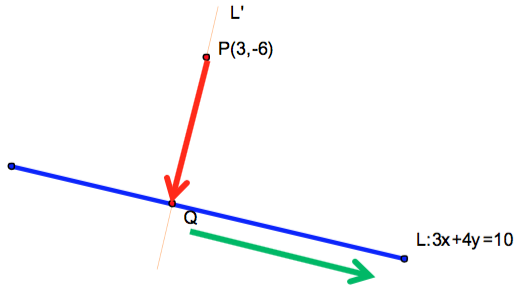
則向量 \(\vec{PQ}=(1-4t,-7+3t)\) 與 \(L:3x+4y=10\) 之方向向量 \(\vec{n}=(4,-3)\) 垂直。(如圖一所示)
因此,內積為 \(4(1 – 4t) + ( – 3)( – 7 + 3t) = 0\),解之可得 \(t = 1\),可得投影點為 \(Q(6,-2)\),則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。評析:這個方法所需先備知識為《第三冊》第3章-直線的方向向量、直線參數式與內積。求距離過程中,亦順便可求出投影點。此方法可推廣至空間中求點到直線距離、投影點問題,亦可用於求空間中兩平行直線距離。
方法2-2:利用向量 \(PQ\) 與 \(L\) 之法向量平行。
利用直線 \(L:3x+4y=10\) 的參數式,
可假設 \(P(3,-6)\) 在 \(L\) 上的投影點 \(Q(2+4t,1-3t)\),
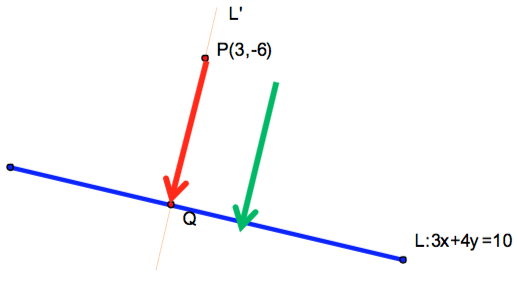
則向量 \(\vec{PQ}=(1-4t,-7+3t)\) 與 \(L:3x+4y=10\) 之法向量 \(\vec{n}=(3,4)\) 平行,(如圖二所示)
利用分量成比例 \(\frac{{1 – 4t}}{{ – 7 + 3t}} = \frac{3}{4}\) 之關係,可得 \(4(1-4 t) = 3 (-7+3t)\),
解之可得 \(t = 1\),可得投影點為 \(Q(6,-2)\),則 \(\overline{PQ}\) 之距離 \(5\) 即為所求。評析:這個方法所需先備知識同樣為《第三冊》第3章-直線的法向量與直線參數式。求距離過程中,亦順便可求出投影點。此法與2-1之差別主要在於利用直線的方向向量與直線的法向量。
方法3:求 \(P\) 點到直線上動點距離之最小值。
方法3-1:利用配方法求 \(P\) 點到直線上動點距離之最小值。
利用直線 \(L:3x+4y=10\) 的參數式,可假設 \(L\) 上任一動點 \(Q(2 + 4t,1 – 3t)\)
則 \(P(3,-6)\) 與 \(Q(2 + 4t,1 – 3t)\) 之距離為:
\(\sqrt {{{(2 + 4t – 3)}^2} + {{(1 – 3t + 6)}^2}}=\sqrt {25{t^2} – 50t + 50}\le\sqrt {25{{{\rm{(}}t – {\rm{1)}}}^{\rm{2}}} + {\rm{2}}5}\le\sqrt {25}{\rm{=5}}\)
即當 \(t = 1\) 時,有最短距離 \(5\),此時 \(t = 1\) 所得之點 \(Q(6,-2)\),
即為 \(P(3,-6)\) 在直線 \(L:3x+4y=10\) 的投影點。(如圖三所示)評析:這個方法所需先備知識為《第一冊》第二章-二次函數配方法求極值、《第三冊》第3章-直線參數式,以及平面上的兩點距離公式。求距離過程中,亦可順便求出投影點。此方法可推廣至空間中,求點到直線距離問題。
方法3-2:利用柯西不等式求 \(P\) 點到直線上動點距離之最小值。
設 \(Q(x,y)\) 為直線 \(L:3x+4y=10\) 上任一點,
則 \(P(3,-6)\) 與 \(Q(x,y)\) 之距離平方為 \(\overline {PQ}= {(x – 3)^2} + {(y + 6)^2}\),
利用柯西不等式 \({(3x – 9 + 4y + 24)^2} \le [{(x – 3)^2} + {(y + 6)^2}({3^2} + {4^2})\),
可得 \({25^2} \le {\overline {PQ} ^2} \cdot 25\),即 \({\overline {PQ} ^2}\) 的最小值為 \(25\),\(\overline{PQ}\) 的最小值為 \(5\)。
且知,當 \(\frac{{x – 3}}{{y + 6}} = \frac{3}{4}\) 時,產生最小值,解之得 \((x,y)=(6,-2)\) ,
即為 \(P(3,-6)\) 在直線 \(L:3x+4y=10\) 的投影點。(如圖三所示)評析:這個方法所需先備知識為《第三冊》第3章-柯西不等式。求距離過程中,亦可順便求出投影點。此方法可推廣至空間中,求點到平面距離問題。
方法4:在直線上任取一點,再利用正射影。
方法4-1:利用在法向量上的正射影長
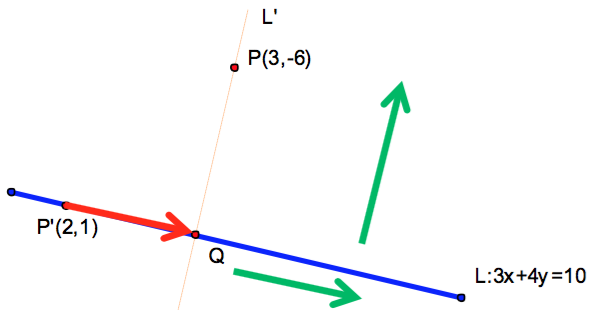
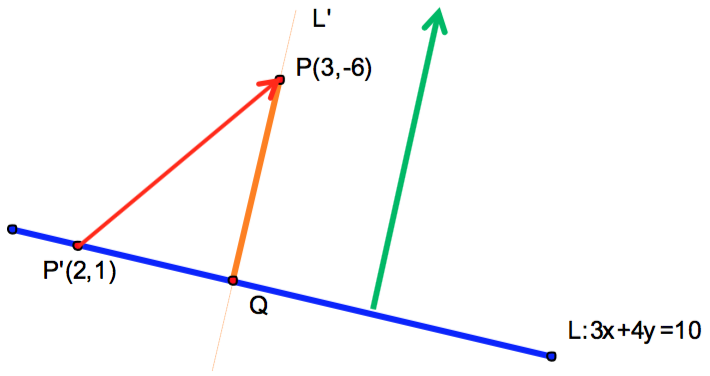
在直線 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\),可得向量 \(\vec{P’P}=(1,-7)\),
\(\vec{P’P}=(1,-7)\) 在直線法向量 \(\vec{n}=(3,4)\) 上的正射影長即為所求。(如圖四所示)
依正射影公式可得正射影為 \(\frac{{(1, – 7) \cdot (3,4)}}{{25}}(3,4) = ( – 3, – 4)\)
則正射影長為 \(5\),即為所求點 \(P(3,-6)\) 到直線 \(L\) 的距離。評析:這個方法所需先備知識為《第三冊》第3章-直線法向量、正射影公式。可推廣至空間中,求點到平面距離問題。
方法4-2:利用在方向向量上的正射影長
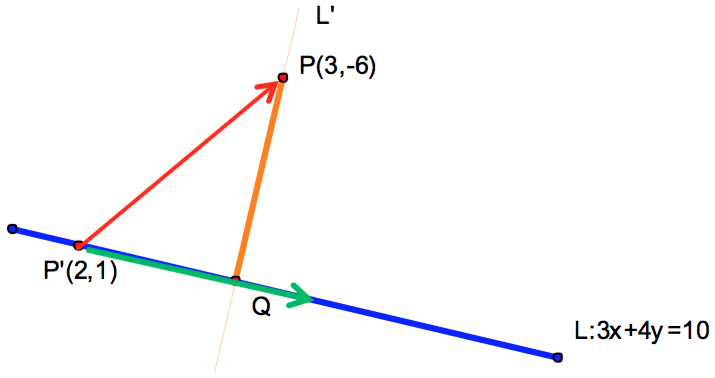
在直線 \(L:3x+4y=10\) 任上取一點 \(P'(2,1)\),可得向量 \(\vec{P’P}=(1,-7)\),
在直線方向向量 \(\vec{L}=(4,-3)\) 上的正射影長為:\(\vec{P’Q}=\frac{{(1, – 7) \cdot (4, – 3)}}{{25}}(4, – 3) = (4, – 3)\)
利用勾股定理 \({\overline {PP’}^2}= {\overline {P’Q} ^2} + {\overline {PQ} ^2}\),可求得點 \(P(3,-6)\) 到直線 \(L\) 的距離為\(5\)。
(如圖五所示)評析:這個方法所需先備知識為《第三冊》第3章-直線方向向量、正射影公式以及國中學過的勾股定理。不過,方法4-2顯然較為簡捷。
以上為三類平面上點到直線距離的解法,接下來的〈平面上點到直線距離(三)〉繼續討論另外三類解法,以及相關知識間的連結。
連結:平面上點到直線距離(三)
- 平面上點到直線距離(一) 2014/09/02
平面上點到直線距離(一) (The distance from a point to a line in the plane Ⅰ)
臺北市立和平高中教師黃俊瑋求平面上一點 \(P(x_0,y_0)\) 點到直線 \(L:ax+by+c=0\) 距離問題,是高中課程中重要而基本的問題,此問題出現在平面向量單元裡,課程中並且提供了公式解:
\(\displaystyle d(P,L)=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
而這個公式 除了可用以推導出平面上兩平行直線之距雄公式之外,亦可推廣至空間中,求一點 \(P(x_0,y_0,z_0)\) 點到平面 \(E:ax+by+cz=0\) 距離問題。
儘管「代公式」的方式簡便而快速,但事實上,除了公式解之外,尚存在許多不同的解法,這些解法分屬於高中坐標幾何、向量幾何與三角學等課程範疇,若不考慮各解法背後的邏輯關係,在學完相關單元後,可以由此問題出發,進行一題多解,將坐標幾何、向量幾何相關單元中的重要概念,作一連結,而當中的許多方法與想法,亦可進一步用於空間中點、線、面相關距離問題。以下,我們以實際問題為例,在本文以及〈平面上點到直線距離(二)〉、〈平面上點到直線距離(三)〉等文裡,提供公式解之外,共七大類,近20種解法,除了討論各類解法所涉先備知識,以及這些方法與空間中相關問題之間的連結。 Continue reading →
- 集合的元素個數:有限與無限 The cardinal number of a set:From finite to infinite 2014/08/28
集合的元素個數:有限與無限 The cardinal number of a set:From finite to infinite
臺北市立和平高中教師黃俊瑋高中課程第二冊裡,介紹了集合相關的基本概念,接著討論了計數有關的加法原理、乘法原理、一一對應原理以及取捨原理等。同時,無論該冊第二章的排列、組合單元或者第三章涉及古典機率、條件機率之計算,皆與集合元素個數的計算有關。說穿了排列組合這門學問,便是討論如何「有系統地」數數、或有系統地計算出集合的元素個數。
不過,在高中的範疇裡,僅限於有限集合的討論,同時也提到,當兩個有限集合的元素之間存在一一對應的關係時,易知這兩個集合的元素個數相等。例如:現有 \(A={1,2,3}\) 與 \(B={a,b,c}\) 兩個集合,我們發現 \(1\leftrightarrow a\)、\(2\leftrightarrow b\) 且 \(3\leftrightarrow c\);亦即,兩個集合的元素可以作一配對,不會重複,且兩邊也都沒有剩下的元素,因此這兩個集合之元素個數相等。教材中,稱其為一一對應原理。當集合元素個數少時,我們易於點算或計數,看不出此原理之大用。然而當計算某集合的元素個數不易時,我們可以尋找另一熟悉的新集合,使得兩集合之元素具有一一對應關係。如此,透過計算新集合的元素個數,求得原集合的元素個數。 Continue reading →
- 重複組合(二):公式的一個直觀解釋 2014/08/27
重複組合(二):公式的一個直觀解釋
Combination with repetition (II):An intuitional explanation of the formula
臺北市立和平高中教師黃俊瑋在〈重複組合(一):相關課程之統整與反思〉一文裡,簡單統整了重複組合相關概念與連結。
一般而言,重複組合問題可利用一一對應原理,轉化成 \(x_1+x_2+\cdots+x_n=k\) 類方程式求非負整數解個數問題,再進一步轉化得其解的數量為 \(C_k^{k+n-1}\)。而各類計數問題,只要轉化成上述方程式求非負整教解問題,便可依此組合公式求解。
以具體的例子來看,從 \(3\) 類物(每類物超過 \(5\) 個)可重複地選出 \(5\) 個的組合數,等於方程式 \(x+y+z=5\) 的非負整數解個數,可轉化成 \(5\) 個○與 \(2\) 個分隔記號|的排列數,再換成組合數,如此可知非負整數解之數為 \(C_3^{5+(3-1)}\)。
這裡筆者分享另一個想法:我們可將分隔記號「|」改以加號「+」代替,這時 的一組解可對應到「○○○○○++」的一種排法,例如:「○○+○○+○」\(\leftrightarrow(2,2,1)\);「○++○○○○」\(\leftrightarrow(1,0,4)\),其中,將球區分成 \(3\) 區同樣需要兩個+號,同時,加號可有助於直觀地與「\(3\) 個變數加起來為 \(5\)」,以及「\(3\) 類球○加起來共選 \(5\) 個」作連結。
- 和算家求橢圓周長的方法(二)(Wasan’s method of finding the formula of the circumference of an ellipse Ⅱ) 2014/09/06
Insert math as
Additional settings
Formula color
Type math using LaTeX
Preview
\({}\)
Nothing to preview
Insert