發現殭屍星球？
高瞻計畫特約編譯 柯廷龍/國立臺灣大學物理學系王名儒教授責任編輯

編譯來源：NASA’s Hubble Finds Supernova Star System Linked to Potential “Zombie Star”

天文學家很可能有機會藉由哈伯望遠鏡發現一種奇妙的現象：在一個微弱超新星(supernova)爆炸之後，留下了一顆與眾不同的「殭屍星球」(zombie star)。

這顆推論的「殭屍星球」原本該是顆白矮星(white dwarf)，它隸屬於星系NGC1309，距離地球1.1億光年。專家們觀測到這顆星球的旁邊有個藍色星球的伴星(companion star)。白矮星從其伴星吸取能量，使得白矮星產生核融合反應(nuclear reaction)並且爆炸。

本圖由上方的白色X符號，標記出NGC 1309螺旋狀星系中的2012Z超新星爆炸發生地點。兩張小圖是由哈伯望遠鏡在超新星爆炸前後捕獲的珍貴照片。(Image Credit: NASA, ESA)

這個超新星的名稱是SN2012Z，於2012年被Lick天文台的超新星搜尋團隊(Lick Observatory Supernova Search）發現。SN2012Z被歸類為Iax型超新星，目前天文學家已經觀測出30多個這種Iax型超新星，因為它的爆炸威力較弱，也有人稱這類現象為迷你超新星(mini-supernova)。

一般的超新星爆炸，通常會讓爆發的恆星毀滅殆盡，不過像Iax型這種超新星爆發，卻會留下苟延殘喘的白矮星。Iax型超新星與Ia型超新星相似，由於後者具有極大且固定的爆發強度，對於衡量宇宙星系間距離及其擴展非常重要。只可惜天文學家們還尚未獲得完整的la型超新星形成資料。所以若能夠觀察到 Iax型超新星的形成方式無疑是一大發現，讓人也能對Ia型超新星的形成機制有旁敲側擊的了解。 Continue reading →

逸散 (Effusion)
國立臺灣大學 物理博士班 97級 鄭安良

當裝有氣體分子的容器外牆有一個微小的孔洞時，容器內的氣體分子會經由這個小洞慢慢的流出容器外。如果這個孔洞非常微小，在容器內氣體分子並不會明顯被改變其原本處於平衡的狀態，此時容器內氣體分子經由此微小孔洞流出到容器外的過程，我們就稱之為逸散(Effusion)。

然而，想要發生逸散的現象，容器的孔洞必須要多小呢？

我們知道平均自由徑 $$l$$ (Mean free path)的長度大約可以看成氣體分子之間自由的移動直到發生碰撞發生之前所走的距離，當氣體分子經過孔洞附近的區域，氣體分子溢出容器時沒有相互發生碰撞，也就是孔洞的直徑 $$D$$ 要小於氣體分子的平均自由徑的長度 $$l~(D<l)$$，這就是發生逸散時孔洞大小的條件。 Continue reading →

RC電路(RC circuit)
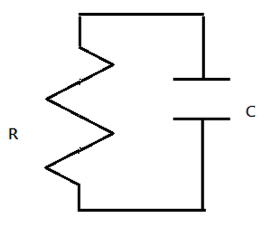
國立臺灣大學物理系 101級 劉仁宇

圖 1 最簡單的RC電路

RC電路顧名思義是由電阻和電容所組成的電路，最簡單的形式如圖 1，該電容已經充電過，可視為一個電源供應器接上一個電阻，如果未充電過則儲存電荷量 $$Q$$ 為零，甚麼事也不會發生。

由於電路滿足克希何夫定律(Kirchhoff’s law)，亦即通過整個迴圈的總電位降為零，故可列式為

$$\displaystyle V=\frac{Q}{C}=IR$$

其中 $$V$$ 為電阻兩端的電壓，$$C$$ 為電容，$$Q$$ 為電容所儲存的電量。

又因為電容的電荷隨時間 $$t$$ 減少產生電流 $$\displaystyle-\frac{dQ}{dt}=I$$

聯立兩式可解得 $$\displaystyle \frac{dQ}{dt}=-\frac{1}{RC}Q$$，

分離變數後積分得 $$\displaystyle Q=Q_0e^{-\frac{t}{RC}}$$，其中 $$Q_0$$ 為一開始電容儲存的電荷量。 Continue reading →

LC電路(LC circuit)
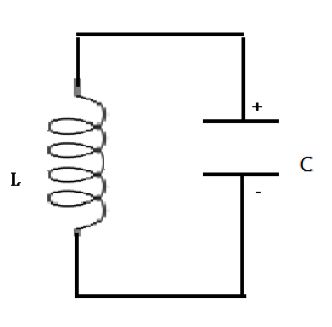
國立臺灣大學物理系 101級 劉仁宇

圖1 最簡單的LC電路

LC電路顧名思義是由電感(inductor)和電容(capacitor)所組成的電路。首先，先介紹最簡單的電路，僅由一個電感和電容所組成，如圖 1。令電容所儲存的電荷量為 $$Q$$、電流為 $$I$$，在整個電路作用的期間可將電容視為一個電源供應器供應電感的電壓，依此列式得

$$\displaystyle V=\frac{Q}{C}=L\frac{dI}{dt}$$

又因為電荷量隨時間的變化量會產生電流，帶入上式後得

$$\displaystyle\frac{d^2Q}{dt^2}=-\frac{Q}{LC}$$

Continue reading →

RLC電路(RLC Circuit)
國立臺灣大學物理系 100級 周結

A Brief Introduction to the RLC Circuit

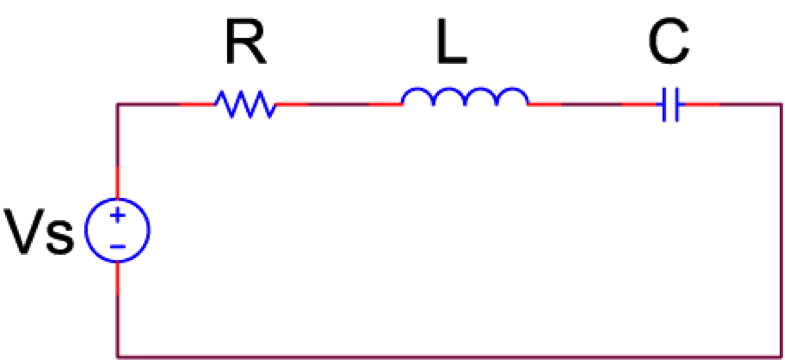
圖(一)的電路是我們要想要了解的典型RLC電路，其中R代表電阻、L代表電感、C代表電容、Vs則代表電壓源。我們想要關心的是，當電壓源的訊號是一個弦波(例如：$$V_0\cos{\omega t}$$)時，這個電路會展現出什麼特性，這些特性又會有什麼用途呢？

圖一 來自於參考文獻2 http://paynesnotebook.net/Research/ElectricalCircuits/SeriesRLC/index.html

也許無法避免的，我們需要算一些數學

$$\displaystyle Ri(t)+L\frac{di}{dt}+\int^{\tau=t}_{0} i(\tau)d\tau=V_0\cos{\omega t}$$

上式沒有特別深奧的道理，只是這個電路遵守的克希何夫電壓定律(Kirchhoff’s voltage law)寫出來的樣子。寫下這條式子後，現在我們要做的，就只是找出什麼樣形式的電流 $$i(t)$$ 會滿足這條方程式，並藉此看出RLC電路的特色與用途。然而，解出 $$i(t)$$ 並不是件簡單的事情。 Continue reading →

來自遠古的超級大地球
高瞻計畫特約編譯 柯廷龍/國立臺灣大學物理學系王名儒教授責任編輯

編譯來源：Exoplanets found orbiting former extragalactic star

來自遠古的流浪者們：卡普坦星和其行星。根據推論，卡普坦星和其行星來自被銀河系吸收掉的一個矮星系。從照片中可以一覽兩星系融合時，星星流動的壯麗景觀。（照片提供者：加州大學的Victor Robles, James Bullock , Miguel Rocha and Joel Primack等人）

由英國倫敦大學瑪莉王后學院Guillem Anglada-Escudé博士所帶領的研究團隊發現了一顆與眾不同的星球dubbed Kapteyn b，這可能是人類所知最古老的適居行星(habitable planet)。

這顆源自太陽系外的星球已經約有115億歲的高齡了，比地球老了約2倍。這個發現讓科學家們改變對適居行星歷史的想法，原來早在遠古就有適居星球的存在。 Continue reading →

如何使用手機產生量子隨機亂數？
國立臺灣大學應用物理研究所 劉伊修編譯/國立臺灣大學物理學系 王名儒教授責任編輯

編譯來源：Physics World- “How to make a quantum random-number generator from a mobile phone” 

將會有可以產生隨機亂數的手機應用程式誕生(Courtesy: Marketa Michalkova)

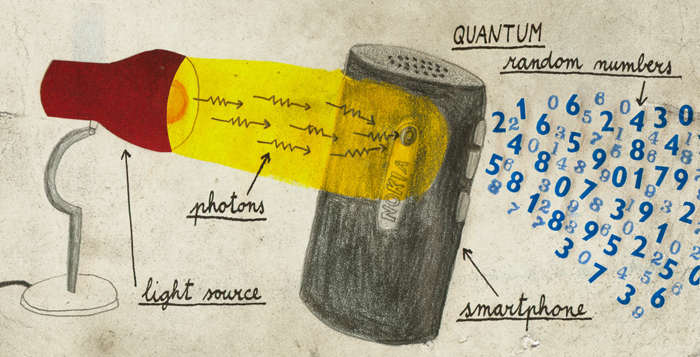
20世紀末，微觀粒子的量子力學性質使得密碼學有新的突破，一些以前傳統密碼學未解的難題被一步一步的解開。其中一個廣為人知的就是量子金鑰傳輸(簡稱QKD)，它的問世使得用網路來傳送極機密的密碼同時又能保有很高的安全性成為可能。但是在使用這個方法時需要用到隨機產生的亂數的序列，也就是真的沒有規律可循的數列。以前使用電腦所產生的隨機亂數被稱做假隨機亂數，它們是如何產生的呢？ Continue reading →

改變歷史進程的17個方程式
臺北市立第一女子高級中學蘇俊鴻老師編譯/國立臺灣大學物理系王名儒教授責任編輯

編譯來源：The 17 Equations That Changed The Course Of History

數學圍繞在我們四周，它在許多方面型塑(shaped)我們對這個世界的理解。

2013年，身為數學家，也是科普作者的伊恩．史都華(Ian Stewart)出版了《改變世界的17個方程式》(The 17 Equations that Changed the World)一書。近來，我們在Dr. Paul Coxon的Twitter (由數學輔導老師，也是部落客的Larry Phillips所註冊)上發現這個他摘錄書中方程式所成的簡便表格： Continue reading →