RLC電路(RLC Circuit)

Posted on 2014/08/25 in 物理, 電流, 電磁學 with 有 1 則留言 18,229 views

RLC電路(RLC Circuit)
國立臺灣大學物理系 100級周結

A Brief Introduction to the RLC Circuit

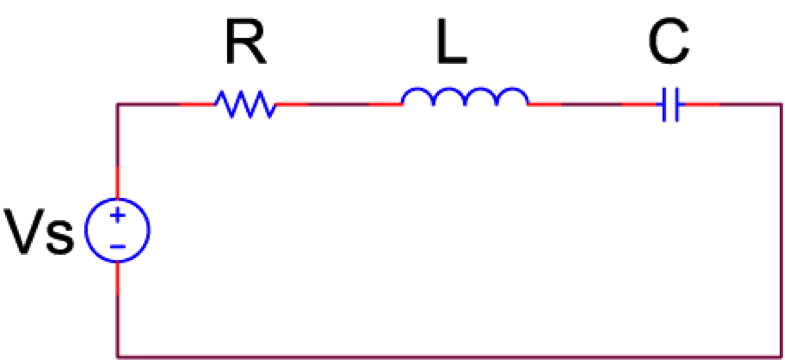
圖(一)的電路是我們要想要了解的典型RLC電路，其中R代表電阻、L代表電感、C代表電容、Vs則代表電壓源。我們想要關心的是，當電壓源的訊號是一個弦波(例如：$$V_0\cos{\omega t}$$)時，這個電路會展現出什麼特性，這些特性又會有什麼用途呢？

圖一來自於參考文獻2 http://paynesnotebook.net/Research/ElectricalCircuits/SeriesRLC/index.html

也許無法避免的，我們需要算一些數學

$$\displaystyle Ri(t)+L\frac{di}{dt}+\int^{\tau=t}_{0} i(\tau)d\tau=V_0\cos{\omega t}$$

上式沒有特別深奧的道理，只是這個電路遵守的克希何夫電壓定律(Kirchhoff’s voltage law)寫出來的樣子。寫下這條式子後，現在我們要做的，就只是找出什麼樣形式的電流 $$i(t)$$ 會滿足這條方程式，並藉此看出RLC電路的特色與用途。然而，解出 $$i(t)$$ 並不是件簡單的事情。

讓我們先定義一些符號以便了解之後的結果。

$$\displaystyle\omega_0=\frac{1}{\sqrt{LC}}$$

$$\displaystyle \beta=\frac{R}{2L}$$

$$\displaystyle\delta=\tan^{-1}{(\frac{2\omega\beta}{\omega_0^2-\omega^2})}$$

跳過繁雜的計算我們可以得到一個不會太難且具有物理意義的結果

$$\displaystyle i(t)=\frac{-V_0}{\sqrt{R^2+(\frac{1}{\omega C}-\omega L)^2}}\sin{(\omega t-\delta)}$$

我們可以從這式子知道些什麼東西呢？

很顯然的，$$i(t)$$ 是一個正弦函數，且與電壓源有著相同頻率但差了一個相位 $$\delta$$，但有趣的是這個函數的振幅：

$$\displaystyle \frac{V_0}{\sqrt{R^2+(\frac{1}{\omega C}-\omega L)^2}}$$

這是一個與 $$R,L,C$$ 值皆有關的函數，暫且讓我們令 $$R,L,C,V_0$$ 皆等於一個單位，先來觀察它和頻率 $$\omega$$ 的關係。

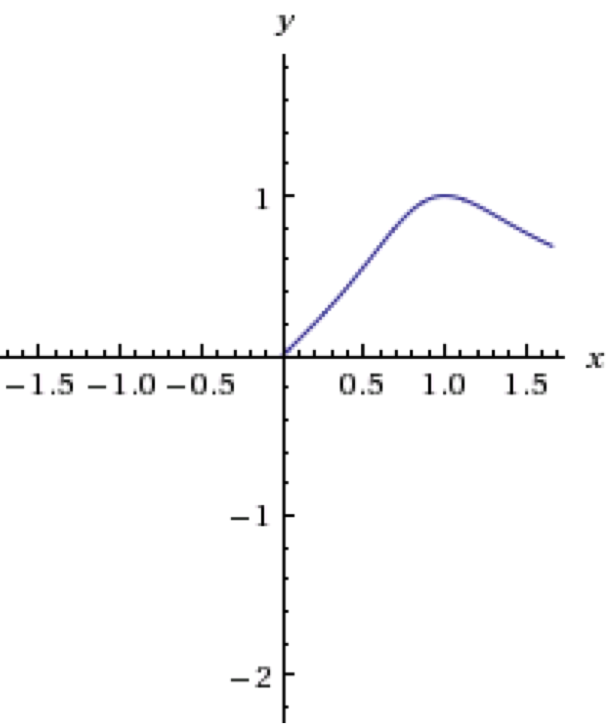
圖二利用Wolfram alpha 平台http://www.wolframalpha.com/繪出，$$y-$$軸為 $$i(t)$$ 的振幅，$$x-$$軸為 $$Vs$$ 的頻率 $$\omega$$

我們可以從圖(二)看出，這個電路電流的振幅竟然會隨著 $$\omega$$ 改變，並且有一個最大值，發生在差不多 $$\omega=1$$，也就是 $$\omega\sim\omega_0$$ 的時候，這是我們覺得有趣的地方。也就是說，這個電路似乎特別喜歡某個頻率，當電壓源的頻率在這個頻率時，整個電路會有最大的電流，就好像是「共振」發生了。而這個特別的頻率則與 $$L,C$$ 的值有關。

那麼，$$R$$ 扮演什麼腳色呢？

我們讓 $$L,C,V_0$$ 維持等於 $$1$$，將 $$R$$ 變為 $$0.5$$、$$0.25$$，則我們可以得到以下結果。

圖三利用Wolfram alpha 平台http://www.wolframalpha.com/繪出，$$y-$$軸為 $$i(t)$$ 的振幅，$$x-$$軸為 $$Vs$$ 的頻率 $$\omega$$

在圖(三)中，我們依然看出振幅的最大值發生在 $$\omega\sim\omega_0$$ 的時候，但我們也另外發現，隨著 $$R$$ 變小，振幅隨著越來越大；這似乎告訴了我們 $$R$$ 是一個限制電流大小的物理量，而這也很合乎我們對電阻的認識。當 $$R=0$$ 時，振幅可以趨近於無窮大！

我們現在認識到了，$$RLC$$ 電路一個很重要的特性就是，面對不同頻率的電壓訊號，會對應產生不同振幅的電流。簡單來說，當很多不同頻率的訊號同時進入這個電路時，一部分的訊號會被減弱，同時另一部份的訊號會被放大。我們可以藉由改變 $$L,C$$ 的數值，決定哪個頻率應該被放大。這便是 $$RLC$$ 電路一個很重要的應用：濾波。

也許你會想說，那麼如果沒有 $$R$$，整體的濾波效果應該會最好吧！但是可惜的是，一個電器、電路裏頭不會沒有電阻；另一方面，電阻也提供了我們一個電流上限的資訊，讓我們知道怎樣的操縱是安全且足夠好的。

參考文獻：