力矩 (Torque)
臺中縣常春藤高級中學物理科李品慧老師/國立彰化師範大學物理學系洪連輝教授責任編輯

力矩

力矩為使物體沿一固定軸或中樞轉動所需的作用，我們常用符號τ來表示。如同可以改變物體運動狀態的作用力，力矩可以想像為使物體扭轉所需的物理量。力矩的大小決定於三個要素：施力、施力點的位置向量以及力與施力位置向量的夾角，因此我們定義力矩為力與力臂的外積。

轉軸至作用力的垂直距離稱為力臂，它的選擇在簡單機械原理中非常重要。力臂愈大，可得愈佳的轉動效果；力臂愈小，產生的轉動效果較小。對一固定的轉軸而言，力矩可能使物體產生逆時鐘方向，或順時鐘方向的轉動。力矩的符號規則一般選取如下：產生逆時鐘方向轉動的力矩取為正號，順時鐘方向轉動的力矩取為負號。

力偶

物體受到大小相等、方向相反而不作用於同一直線上的兩力，此兩作用力稱為一對力偶，力偶產生的力矩稱為力偶矩。

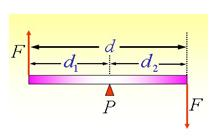
如圖，量值同為F而方向相反的兩力，分別垂直作用於一棒子的兩個不同位置，對兩力作用點之間的 任意一點P，分別造成力矩Fd1和Fd2，由於這二個力矩的效果都是使棒發生同一個方向轉動，故合力矩為：

τ=Fd1+Fd2=F(d1+d2)=Fd

式中d為兩力的垂直距離，稱為力偶臂。因為P點為任意選取，可見力偶矩不論對哪一個軸，其量值都相同。

轉動平衡

當數個力矩同時作用在一個物體上，使其繞某一軸轉動時，整體的轉動效果等於數個力矩的向量和。若數個力矩的向量和為零時，物體不會改變其轉動狀態，此時我們稱物體處於轉動平衡，即物體所受順時鐘方向的合力矩量值，等於逆時鐘方向的合力矩量值。

參考資料
http://en.wikipedia.org/wiki/Torque

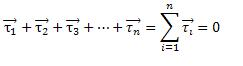
都卜勒效應（Doppler Effect）
國立臺南第一高級中學物理科王俊乃老師/國立彰化師範大學物理學系吳仲卿教授責任編輯

都卜勒效應又稱為都卜勒偏移(Doppler shift)，該效應首先由奧地利物理學家Christian Andreas Doppler在1842年發表。根據都卜勒效應，與波源具有相對速度的觀察者，觀察到的波動之頻率產生了變化。例如，一輛車上佩帶有警報器的汽車，當警報器發出聲音時，車子接近、通過或者是遠離觀察者時，都會產生都卜勒效應。當汽車接近觀察者時，觀察者接收的聲波頻率比發射頻率高；當汽車遠離觀察者時，觀察者接收的聲波頻率比發射頻率低。

針對聲波這一類在介質中傳遞的波動，都卜勒效應是來自於聲源的運動(motion of the source)、觀察者的運動(motion of the observer)以及介質的運動(motion of the medium)等因素。上述運動變因產生的影響，必須分開來分析。但是，像光波，或者是特殊相對論裡頭的重力波(gravity in special relativity)，因為都不需要依靠介質傳播，所以都卜勒效應只受觀察者與聲源之間的速度的相對差異影響。

資料來源：
http://en.wikipedia.org/wiki/Doppler_effect

分貝（Decibel, DB）
國立臺南第一高級中學物理科王俊乃老師/國立彰化師範大學物理學系吳仲卿教授責任編輯

分貝是一個對數單位(logarithmic unit)的測量值，用來表示相對於某一特定程度的物理量(通常是功率power或者是強度intensity)大小。因為分貝是兩個具有相同單位的物理量的比值，所以分貝是沒有單位的物理量(dimensionless unit)。分貝是另外一個物理量─貝(bel)的十倍，貝是一種音量比率的單位，算是很少見的單位。

在科學研究，或者是工程領域(engineering)，分貝在測量的應用上都具有很廣大的用途，尤其是聲學(acoustics)、電子學(electronics)和控制裡論(control theory)。例如，使用分貝可以很方便地表達很大或者是極小的數字，而且分貝的對數尺度也大約地對應人類對於光學與聲音的認識。此外，對數也有利於使用簡單的加法與減法就處理比值的乘法運算(multiplication)。

為了顯示分貝是對應哪一個參考量(reference quantity)或是頻率權值函數(frequency weighting function)，分貝符號常常會添加字尾，例如”dBm”，代表參考量是毫瓦milliwatt，至於”dBu”，則代表參考量是0.775 volts RMS。至於分貝與貝的定義，都是使用以10為底的對數。另一個很相似的比值物理量，稱之為neper，則是以自然數為底的對數。

資料來源：
http://en.wikipedia.org/wiki/Decibel

動能（Kinetic Energy）
台中縣常春藤高級中學物理科李品慧老師/國立彰化師範大學物理學系洪連輝教授責任編輯

物體運動時所擁有的能量稱為動能（Kinetic Energy）。動能也常被定義為當某物體由靜止狀態轉變為此運動速率的狀態所需要的功（Work）。物體運動時是依據速率的改變而產生不同的動能大小，換句話說，一個物體的動能只有在速率改變時才會跟著改變。
１９世紀中期，一位法國數學、科學、工程學家科里奧利（Gaspard-Gustave de Coriolis）是第一位提出「功」和「動能」的觀點。１８９２年，科里奧利出版一本以數學理論觀點進一步說明動能的書—「Du Calcul de l’Effet des Machines」。書中他對動能的定義為物體質量的二分之一乘其速度的平方（KE=mv²/2）。幾十年後，同是數學物理學家、工程師的威廉湯姆森（William Thomson）更進一步驗證科里奧利的想法是正確的。 Continue reading →

萬有引力（Universal Gravitation）
台中縣常春藤高級中學物理科李品慧老師/國立彰化師範大學物理學系洪連輝教授責任編輯

萬有引力定律為經驗性的定律，是古典物理學中的一環，牛頓在1687年於「自然哲學的數學原理」發表此定律，描述有質量二物體間的吸引力。
任意二個質點通過連心線方向上的力相亙吸引，該引力的大小與他們的質量乘積成正比，與他們的距離平方成反比，與二物體的化學本質或物理狀態以及中介物質無關。其

公式為：
萬有引力常數G值是由英國著名的科學家卡文迪西(Henry Cavendish, 1731-1810)，在實驗室中利用兩對鉛球，每對大小各一，測量每對鉛球之間的萬有引力對小鉛球連桿產生的力矩而測出。這是牛頓的萬有引力理論的第一個實驗，與牛頓提出理論時相距111年，也是牛頓死後71年，因此牛頓當時只能推導出兩力之間的關係，並不能算出實際的數值。

重力加速度：
設a1為一質點的重力加速度，由牛頓第二定律F=m1a1 ，即a1=F/m1
以萬有引力取代式中的F，則
a1=Gm2/r2
同理亦可得出a2，重力加速度的SI制單位為米每平方秒(m⁄s2)。
我們可以發現重力加速度的值與m1的大小並無關聯，因此如果忽略空氣阻力，任何物體，無論質量為多少，都將以同樣的重力加速度向地面墜落。如果物體運動過程中，r只有極微小的改變，如地面附近的自由落體運動，重力加速度將幾乎保持不變；然而對於龐大的物體，由於r的變化導致不同位置所受的重力變化，則會引起巨大而可觀的潮 汐力作用。

參考資料：
http://en.wikipedia.org/wiki/Universal_gravitation

達維生-革末實驗（Davisson–Germer Experiment）
國立臺中女子高級中學物理科陳正昇老師/國立彰化師範大學物理學系吳仲卿教授責任編輯

1927 年達維生(Clinton Davisson)與革末(Lester Germer)在美國貝爾實驗室合作完成了這個支持德布羅意物質波理論的實驗。從歷史上來看，這個實驗所展現的波粒二象性對於建立量子力學以及薛丁格方程式具有無比重要的地位。因為這項重大的貢獻，戴維森和喬治-湯姆森一起榮獲 1937 年的諾貝爾物理學獎。 Continue reading →

螺線管（Solenoid）
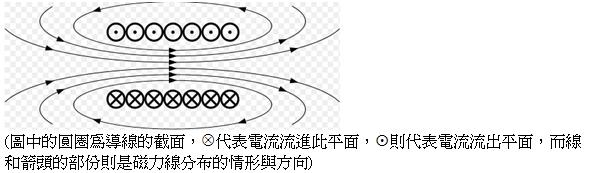
台中縣立中港高級中學物理科王尊信老師/國立彰化師範大學物理學系洪連輝教授責任編輯

所謂的螺線管，指的是由一質地均勻的金屬導線，所纏繞而成的金屬線圈，若現在有一電流通過，螺線管便會產生磁場，如下圖

若流入平面的導線中間有一點 $$P$$，根據安培右手定則，$$P$$ 點左邊的導線會給予 $$P$$ 點向下的磁場，而 $$P$$ 點右邊的導線則會給予向上的磁場，大小相等但方向相反，彼此互相抵消，最後的結果，便如圖所示，我們可以根據安培右手定則知道內部磁場的方向，四指彎曲指向電流方向，此時大拇指所指的就是內部磁場的方向。若此螺線管纏繞的非常均勻、緊密，且長度遠大於口徑，則內部的磁場便可視為均勻分布。 Continue reading →

質譜儀 (Mass Ｓpectrometry)
臺中縣立中港高級中學物理科王尊信老師/國立彰化師範大學物理學系洪連輝教授責任編輯

所謂的質譜儀，是一種能夠判別樣品的元素組成或分子的分析儀器，其原理主要是利用離子之荷質比的不同，加以分離各個離子，並測量其分子量。
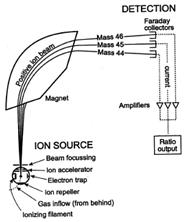
下圖為質譜儀之簡易構造圖。

質譜儀之構造主要分成五個部份:樣品導入系統、離子源(ion source)、質量分析器(mass analyzer)、偵測器(detector)、質量處理系統(data analysis)。首先，我們利用導入系統將樣品導入，這些樣品會在離子源的地方產生電離，被分解成離子態，再藉由電場加速正離子之運動(電場方向會決定打出去的離子是帶正電或負電，在此，我們利用的是正離子)，使正離子變成離子束，打向質量分析器，而分析器處設有一個磁場，這些正離子在磁場中會受到垂直速度方向的磁力影響，因為荷質比的不同，造成之磁力便會不同，因此，各個正離子會根據不同磁力所造成的軌跡前進，接著撞擊在偵測器上，當離子撞擊偵測器時，連接著偵測器的電線會提供電子，用以中和離子使其恢復電中性，這些電子在電線上不斷移動，使電線產生電流，最後，質量處理系統根據這些電流大小進行分析，便可知道分離出來的粒子為何了。 Continue reading →