- v=5/2 量子霍爾態之謎（中） 2019/01/24
v=v=5/2 量子霍爾態之謎（中）
蕭維翰誰是描述v=5/2基態的波函數？曾經我們都快要相信就是 Pfaffian 波函數，直到 …… 。
Figure1. 2+1 維流體中可能的漩渦組態。（photo credit: 作者自繪）
誰是描述v=5/2基態的波函數？曾經我們都快要相信就是 Pfaffian 波函數，直到 …… 。
在前文中我們複習了量子霍爾效應，並在文章的下半段介紹 \(\frac{5}{2}\) 態，並說明為什麼他是個有趣的問題，並且用一個問題結尾 —— 我們有沒有一個類似 Laughlin 波函數的試驗波函數來代表這個狀態。而在本文中我們將更深入地討論這個懸問。
在這之前，筆者想先釐清前文的一段敘述。
- v=5/2 量子霍爾態之謎（上） 2019/01/24
v=5/2 量子霍爾態之謎（上）
蕭維翰v=5/2到底發生了什麼事？這是研究霍爾效應的學者們近年來最關切的問題之一。
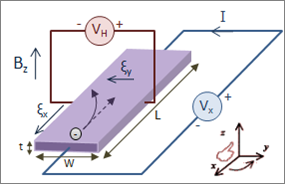
筆者曾用了三四篇文章來討論霍爾效應。從經典的整數量子霍爾效應（IQHE）、分數量子霍爾效應（FQHE）、複合費米子（Composite Fermion）到最近重新掀起討論的 \(v=\frac{1}{2}\) 費米液體態（Fermi Liquid）。在本文中筆者想延伸這些故事，討論另一個實驗上被觀測到的著名的偶數分母的量子霍爾態——\(v=\frac{5}{2}\)，以及它所牽涉的謎團。
然而筆者必須先在此自白：量子霍爾效應並不算是最好的科普題材。儘管這個問題的組成元素很基本：電子、庫倫作用與垂直的磁場。但真的要進行定量說明的時候，我們很難避免討論一些比較生硬的概念，比如說磁通量附著（flux attachment）與測試波函數（trial wavefunction）。而且事實上除了一些拓樸性質，譬如電導率的係數 v，即便最前沿的計算也很難給出很好的解析結果。絕大多數我們必須倚賴數值計算，從而失去一些直覺。 Continue reading →
- 物理學中的對偶性(下) 2018/10/29
物理學中的對偶性(下)
蕭維翰連結：物理學中的對偶性(上)
對偶性不只存在在前面的簡單例子中，其實我們也有費米子與玻色子、玻色子與玻色子、乃至於費米子與費米子間的對偶性。
圖一：水波中的孤波（photo credit: Wikipedia）
在上集的討論中，我們約略介紹了「對偶」（duality）在物理學中，的意思：表面上看起來不同的兩個理論，本質上提供一樣的描述。最基本的例子是所謂伊辛模型（Ising model）在原晶格與對偶晶格上的對偶，以及電磁學馬克斯威方程式（Maxwell equations）在沒有電荷下電場磁場交換的對偶性。 Continue reading →
- 物理學中的對偶性(上) 2018/10/29
物理學中的對偶性(上)
蕭維翰無論在文學或科學的場合，對偶性的追求，都不僅是形式美的提升，而是對所欲描繪的物件做出更深刻表述的嘗試。
An illustration of magnetic monopole. Photo Credit: Heikka Valja. This photo is adopted from the new “Physics Professor David Hall and Team Observe Quantum-Mechanical Monopoles” on Amherst College official website. News Date: 4/30/2015.
筆者希望以這兩年火紅的對偶描述為量子霍爾效應作小結，但在這之前，有必要另開篇幅跟大家聊聊所謂的對偶是什麼。
對偶是漢語傳統文學的一種修辭技術，又稱對仗，常以字數相符的句子兩兩配成（若討論元曲，也可見三句配成的鼎足對）依據創作體裁的不同，在配對的格律要求會略有出入，但詞性相匹，聲韻相對是基本原則，一個雋永的例子是晏幾道一闋臨江仙的首對「夢後樓臺高鎖，酒醒簾幕低垂。」[1]。 Continue reading →
- 【物理世界】量子霍爾效應（四）：迪拉克複合費米子 2018/10/22
【物理世界】量子霍爾效應（四）：迪拉克複合費米子
蕭維翰這兩年物理學家提出了新的粒子電動對稱的理論解釋最低蘭道階（Landau Level）的物理，此新模型不再透過將磁通量附著到原粒子身上，而是藉由粒子漩渦對偶性，用更自然的方法去闡述一些實驗上觀測到的現象。
圖一：在最低蘭道階中的粒子電洞轉換。\(\nu\) 填滿態會被轉換到 \(1-\nu\) 填滿態，而 \(\nu =\frac{1}{2}\) 擁有粒子電洞的對稱性。
在前面幾篇文章中，我們介紹了量子霍爾效應的現象，並為分數與整數量子效應提供一些解釋。再者我們討論了 Jain 的複合費米子理論，指出實驗上觀測到的分數 \(\frac{1}{3},~\frac{2}{5},~\frac{3}{7},…\) 或 \(\frac{2}{3},~\frac{3}{5},…\) 等，都能被 Jain 序列所說明。在結尾處，我們指出 Jain 序列的極限是 \(\frac{1}{2}\)，在那個狀況下，複合費米子看不到磁場，並形成一個費米液體。針對這個問題， HLR 是一個知名的有效理論。 Continue reading →
- 【物理世界】量子霍爾效應（三）：複合費米子 2018/10/22
【物理世界】量子霍爾效應（三）：複合費米子
蕭維翰連結：【物理世界】量子霍爾效應（二）：分數量子化與 Laughlin 波函數
在 Laughlin 波函數後，J. Jain 提出了複合費米子的概念，將整數量子霍爾效應與分數量子霍爾效應結合在一個框架下，並成為研究量子霍爾效應的一個典範。
本圖引自1990年6月22《科學》雜誌封面，courtesy of illustration T. S. Duff and T. Kovacs, AT&T Bell Laboratories
儘管 Laughlin 波函數從定量的角度提供了當時人們了解某些分數霍爾態的出發點，它並不稱得上是一個完整的「故事」。另一方面，它的成功也多侷限於 \(\frac{1}{3},~\frac{1}{5}\) 等分數，而不涵蓋其他如 \(\frac{2}{5},~\frac{3}{7}\) 等也在實驗中被發現的狀態。 Continue reading →
- 【物理世界】量子霍爾效應（二）：分數量子化與 Laughlin 波函數 2018/10/15
【物理世界】量子霍爾效應（二）：分數量子化與 Laughlin 波函數
蕭維翰在前一篇筆者討論了整數的量子霍爾效應，也就是實驗中測得電導率的xy分量為電荷平方除以普朗克常數的整數倍。我們雖然沒有篇幅涵蓋實驗上所看到現象的所有必要物理概念，但至少有一個很概略的圖像：整個系統像一個公寓，公寓的樓層叫蘭道階，愈底層的公寓房租（能量）愈低，所有的電子便從第一層公寓築起，並且電子遵循庖立不相容原理（Pauli exclusion principle）所以一間房間只能住一個電子，實驗上這些整數對應到住滿的蘭道階的階數。[1] Continue reading →
- 【物理世界】量子霍爾效應（一）：塵埃中洗滌出的整數 2018/10/15
【物理世界】量子霍爾效應（一）：塵埃中洗滌出的整數
蕭維翰真的要寫量子霍爾效應，可以寫好幾本書，要從最尖端的進展切入，也會讓讀者摸不著頭緒，這邊我分稿從歷史的起源開始，並只挑一些聽起來真的可以令所有人驚訝的面向。
圖一：霍爾效應的實驗圖示，原本往 x 方向流的電賀受到磁場的影響在 y 方向也形成電壓，變成實驗上可以測量的霍爾電壓, credit: wikipedia
筆者儘管基於工作很常算數學，但上大學後幾乎不常親自動手做數字計算了。前幾個月我在電腦上送出一個滿複雜的積分，幾秒後我得到
\(\displaystyle\frac{-12.56637062125499}{4\pi}\)
不知道讀者們平常做算術的頻率如何，在作業中遇到這種數字會不會覺得很沮喪？分子那一串數字已經無跡可尋，何況底下還除一個 \(4\pi\)？然而有趣是，在電腦有效的位數下，這個組合其實跑出了── \(-1.00000000000000\)
- v=5/2 量子霍爾態之謎（上） 2019/01/24