LC電路(LC circuit)

LC電路(LC circuit)
國立臺灣大學物理系 101級 劉仁宇

圖1 最簡單的LC電路

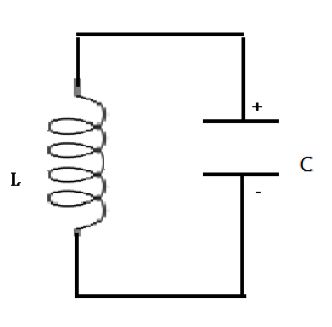
LC電路顧名思義是由電感(inductor)和電容(capacitor)所組成的電路。首先，先介紹最簡單的電路，僅由一個電感和電容所組成，如圖 1。令電容所儲存的電荷量為 $$Q$$、電流為 $$I$$，在整個電路作用的期間可將電容視為一個電源供應器供應電感的電壓，依此列式得

$$\displaystyle V=\frac{Q}{C}=L\frac{dI}{dt}$$

又因為電荷量隨時間的變化量會產生電流，帶入上式後得

$$\displaystyle\frac{d^2Q}{dt^2}=-\frac{Q}{LC}$$

至於負號是怎麼出現的呢？可以想想看如果電容放電，則 $$\frac{dQ}{dt}$$ 為負，若取逆時針方向之電流為正，此時必須加上一個負號，即 $$\frac{dQ}{dt}=-I$$，微分後帶入可得上面的式子；那如果取順時針方向之電流為正，這時 $$\frac{dQ}{dt}=I$$ ，而電感因為電流的方向定義和之前相反而有相反的電位，故 $$V=\frac{Q}{C}=-L\frac{dI}{dt}$$ ，聯立解得 $$\frac{d^2 Q}{dt^2}=-\frac{Q}{LC}$$ 與取順時鐘方向得到的式子相同。

上式是一個二階微分方程，它的解是一個振盪的函數，

如同彈簧簡諧運動 $$m\ddot{x}=-kx$$，其角頻率 $$\omega_0=\frac{1}{\sqrt{LC}}$$，週期 $$T_0=2\pi\sqrt{LC}$$。

圖2 將交流電壓源與LC電路串聯

LC電路一個常見的應用是作為電流放大器。

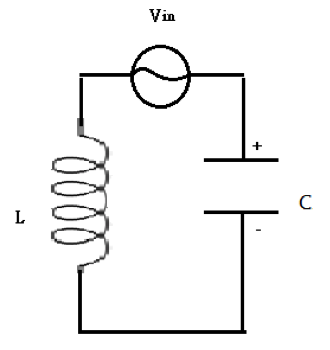
考慮圖 2，在LC電路上加了一個交流電源，

其輸入電壓 $$V_{in}=V_0e^{i\omega t}$$ 為一正弦波。

電路中的電流 $$I=\frac{V_{in}}{Z}$$，

其中總阻抗 $$Z=i\omega L+\frac{1}{i\omega C}$$，帶入上式得

$$\displaystyle I=\frac{V_0e^{i\omega t}}{i\omega L+\frac{1}{i\omega C}}=\frac{\omega CV_0e^{i\omega t}i}{1-\omega^2LC}=\frac{\omega CV_0}{1-\omega^2LC}e^{i(\omega t+\frac{\pi}{2})}$$

由上式可知電流相角較電壓提前或落後 $$90$$ 度（視 $$1-\omega^2LC$$ 的正負號而定），

而電流振幅 $$\displaystyle I_0=\frac{\omega CV_0}{1-\omega^2 LC}$$ 最大值發生在 $$\omega=\omega_0=\frac{1}{\sqrt{LC}}$$，此時發生共振，電流振幅趨近於無限大。所以透過控制輸入電壓的頻率就可以得到不同的電流輸出振幅，達到電流放大的效果。

圖3 將交流電流源與LC電路並聯

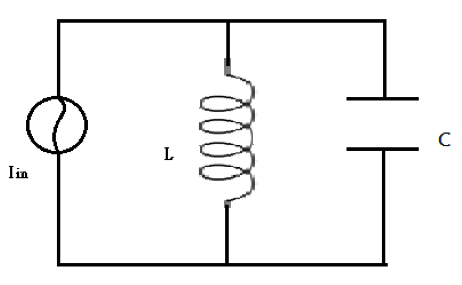
接下來考慮圖 3，為一並聯之LC電路，可作為電壓放大器。這次電源採用交流電流 $$I_{in}=I_0e^{i\omega t}$$，而LC並聯電路的阻抗

$$\displaystyle Z=(i\omega C+\frac{1}{i\omega L})^{-1}=\frac{i\omega L}{1-\omega^2 LC}$$

利用上兩式可解得電源兩端之電壓

$$\displaystyle V=IZ=\frac{i\omega L}{1-\omega^2LC}I_0e^{i\omega t}=\frac{\omega LI_0}{1-\omega^2LC}e^{i(\omega t+\frac{\pi}{2})}$$

故可知電壓相角較電流提前或落後 $$90$$ 度（一樣視 $$1-\omega^2LC$$ 的正負號而定），而電壓振幅 $$V_0=\frac{\omega LI_0}{1-\omega^2LC}$$ 最大值發生在 $$\omega=\omega_0=\frac{1}{\sqrt{LC}}$$，此時發生共振，電流振幅趨近於無限大，透過控制輸入電流的頻率就可以得到不同的電壓輸出振幅，達到電壓放大的效果。

上述的第一個例子說明了LC電路具有一個自然頻率，透過選擇適當的L和C值便可將電路應用在如收音機的頻率接收，保留下想要接收的頻率範圍，抑制其他頻率的雜訊。第二個例子則說明了輸入交流電壓，可以利用共振的特性，在輸入訊號頻率接近自然頻率時，將電流放大許多。(事實上電流並不會變得無限大，因為電路中還有導線的電阻、電源的內電阻、甚至是電感電容也會有內電阻，雖然其值很小但當電流很大時，它的分壓 $$V=IR$$ 也會變得很大，因此不可忽略，故必須使用RLC電路的模型來處理，結果是電流很大但不會趨近於無限大。)

最後，在第三個例子中，是採用與先前兩個相同的原理，但改用電流源，當輸入頻率很接近固有頻率時，電壓會被放得很大，因此可當作電壓放大器，但是電壓峰值一樣不會變成無限大，原因跟上一個例子一樣，都是因為電阻的存在。

參考文獻

1. Sedra A. S.,Smith K. C.(2009), Microelectronics Circuits, Oxford University Press.
2. 2009年國際物理奧林匹亞競賽國家代表隊選訓教材第二冊（物理奧林匹亞國家代表隊選訓工作委員會）.
3. 維基百科. LC circuit. http://en.wikipedia.org/wiki/LC_circuit