帕松亮點 (Poisson Spot)
國立苑裡高級中學物理科王建揚老師/國立彰化師範大學物理學系吳仲卿教授責任編輯

一道光垂直照射在銅板上，在銅板後方會出現什麼樣的影子呢？如果你的答案是圓形的影子，那麼你的意思就是，當你站在本影的中心時，應該完全看不到光源吧！恭喜了！你的答案與17世紀著名的法國數學家及物理學家帕松（Simeon D. Poisson）的看法完全相同。只是如果依照惠更斯（Christian Huygens）光的波動說，光應該像聲波一樣，遇到障礙物會轉彎（繞射），障礙物後的觀察者應該還是看得到光！

通常教科書在介紹波動光學時，都會藉由水波槽實驗及楊氏雙狹縫干涉實驗的說明及演示，來建立光的波動說概念，只是水波與光在日常生活的經驗中，終究是兩種性質截然不同的現象，實在很難順利的說服學生相信光的波動說，而光的干涉實驗又如同魔術師的表演，只是讓人覺得不可思議，主觀上還是採取不相信的態度，因此在這種信心危機下，學習與思考都需要一段長時間的自我說服，或者利用以子之矛，攻子之盾的技巧，才有辦法破除某些迷思概念。

人類在光學的發展史上，也遭遇到類似的情形，此時帕松亮點的質疑與解決，對於光的波動說地位，產生了決定性影響。

雖然第一位挑戰光粒子說的學者湯姆士‧楊 (Thomas Young)，早在1802年已經完成了著名的楊氏雙狹縫實驗，證明光具有水波或聲波的性質，但卻未能說服大英科學組織 (British Scientific Establishment)及其他科學家完全相信光具有波動性。數年後，年輕學者菲涅耳 (J. A. Fresnel)獨立重覆了類似的狹縫干涉實驗，進一步推演出相關的數學理論之後，仍未能使當時的科學前輩完全信服。此時巴黎學會 (Paris Academy)以繞射作為1918年獎賞論文的主題，希望能藉此澄清光的粒子說和波動說所引起之爭辯。

菲涅耳也遞出他的論文參賽，而且表現非常突出，可以獲獎，但是當時評審委員會的主席帕松，認為波動說是錯誤的理論，因此菲涅耳不應獲獎，為了反駁波動說，還根據菲涅耳的理論計算推導出了一個荒謬現象：如果光具有波動性，當一點光源發出的光被一圓形不透明物體遮擋後，從圓形物體邊緣繞射的光，到達圓形物體的陰影中心時，因光程相同，應該會發生建設性干涉，如此一來，日常生活直覺上影子最暗的地方應該有一個亮點！

帕松很清楚的想要以子之矛，攻子之盾。不料，菲涅耳和另一位評審委員阿拉苟（Arago）過不久便以實驗證實了確有這麼一個不尋常的亮點在影子中心，如下圖。

帕松反而無意間提出一簡明的實驗，證明光的波動性。從此之後，光的波動性就逐漸為人們所接受了。後世就稱這個亮點為帕松亮點（Poisson spot）。

參考資料
周鑑恒，Poisson亮點的小掌故，科學月刊全文資料庫，1999年8月第 356期

中子（Neutron）
國立臺中女子高級中學物理科陳正昇老師/國立彰化師範大學物理學系吳仲卿教授責任編輯

中子是一種電中性的次原子粒子，具有比質子稍微大一點的質量。大多數的中子都是處在原子核中，原子核幾乎都是由質子與中子所組成(唯一的例外是氫核，它僅由一個質子構成)，所以質子與中子也被稱為核子。質子數決定了原子序，質子數與中子數的和決定了質量數。同一種元素的原子若具有不同的中子數，則會造成所謂的同位素。例如C-12具有6顆質子與6顆中子，但C-14具有6顆質子與8顆中子。

在穩定的原子核中的中子也是穩定的，但是在原子核外，一顆自由中子的性質是不穩定的。自由中子會透過所謂的衰變而轉換成一顆質子，同時伴隨釋放出一顆電子和一顆反微中子，半衰期大約爲15分鐘(或885.7 ± 0.8 秒)。自由中子常常是來自核分裂或融合的過程。

1930 年Walther Bothe和Herbert Becker在德國發現，如果來自釙的高能量天然α粒子落在鈹、硼或鋰這些較輕的元素時，便會有一種穿透力異常地高的輻射產生。起初這輻射被認為是射線，儘管這種輻射的穿透力比當時已知的任何射線還要大，而且實驗結果的細節很難解釋這個假設。1932 年另外一份關於中子研究的重要報告由Irène Joliot-Curie 和Frédéric Joliot在巴黎提出。他們表示，這未知的輻射如果落在含有石蠟或其他含氫的化合物時將會射出高能的質子。這個現象並不是不符合此新輻射假定的伽瑪射線的本質，但詳細的、定量的分析數據卻使得越來越難與這樣一種假設相吻合。

終於在1932年，物理學家詹姆斯-查德威克在英國的利物浦大學執行了一系列的實驗，證實射線的假說是真的站不住腳了。他建議應該將此新輻射視為由大量的電中性微粒所組成，且中性微粒的質量近似於質子，他緊接著又執行了一系列的實驗來證實他的建議。這種電中性的微粒最終被命名為中子。

中子屬於重子類，由兩個下夸克和一個上夸克構成。以往曾經將中子列為基本粒子的一員。但現今在標準模型理論下，因為中子是由夸克組成，所以它是個複合粒子。
中子和其他常見的次原子粒子最大的分別在於，中子因其下夸克和上夸克之電荷互相抵消，本身不帶電荷。另外，它穿透性強，無法直接進行觀察，也令它在核轉變中成為非常重要的媒介物。這兩項因素使得它在次原子粒子發展歷史的較後期才被發現。

參考資料:
http://en.wikipedia.org/wiki/Neutron

法蘭克(James Franck)-赫茲(Gustav Ludwig Hertz)實驗
國立臺中女子高級中學物理科陳正昇老師/國立彰化師範大學物理學系吳仲卿教授責任編輯

赫茲實驗在近代物理的發展進程中是支持波耳氫原子模型的一個強而有力的實驗年德國的物理學家法蘭克(James Franck)和赫茲(Gustav Ludwig Hertz)想要利用實驗的方法找到原子能階的證據，經過一番努力，他們發表了現在名為「法蘭克赫茲實驗」的實驗成果，這個結果非常明確簡潔地說明了原子內部的確存在著某些特定的不連續的能階。法蘭克赫茲實驗證實了波耳量子化的原子模型，對於後來量子物理的發展，具有很大的貢獻。因為這項工作，法蘭克和赫茲兩人共同分享了1925年的物理諾貝爾獎

這個經典實驗的主要實驗儀器是一個類似真空管的管狀容器，內部充以低壓的水銀蒸氣。這個管狀容器內還安裝了三個電極：發射電子的陰極，網狀用以加速電子的柵極，以及收集電子的陽極。陰極的電位低於柵極跟陽極的電位，而陽極的電位又稍微低於柵極的電位。陰極與柵極之間的加速電壓是可以調整的。從陰極發射出來的電子，由於加速電壓作用，往柵極移動的速度和動能會增加。到了柵極，有些電子會被吸收；有些則會繼續往陽極移動。通過柵極的電子，必須具有足夠的動能，才能夠抵達陽極；否則，會被柵極吸收回去。與陽極線路串聯的安培計可以測量抵達陽極的電流。 Continue reading →

狹義相對論簡介（Special Relativity）
國立臺中女子高級中學物理科陳正昇老師/國立彰化師範大學物理學系吳仲卿教授責任編輯

狹義相對論是1905年愛因斯坦在一篇名為「論運動體的電動力學」的論文中所提出的物理理論。在這一篇論文中愛因斯坦重新思考了在物理學中關於空間與時間的概念以及這兩者之間的關係，並將本來僅適用於牛頓力學中的伽利略相對性原理擴充到電磁學的領域，也就是讓馬克士威的電磁方程式對不同的慣性座標系具有相同的形式。 Continue reading →

檢流計 (Galvanometer)
臺中縣立中港高級中學物理科王尊信老師/國立彰化師範大學物理學系洪連輝教授責任編輯

所謂的檢流計，是一種可以測量電路中電流的電流計，其原理裝置圖如下：

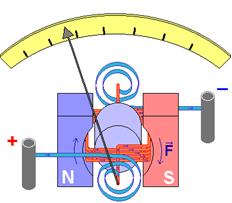
如圖所見，中間是一個鐵製的圓柱，上面纏有 $$N$$ 匝的線圈，並由永久磁鐵環繞包覆，最後線圈再連接指針和一個渦形的彈簧。如此一來，導線通有電流時，會產生一個向下的磁力（大拇指指向電流方向、四指指向磁場方向、掌心指向受力方向，而圓柱頂面的導線平行磁場，故不產生磁力，產生的是圓柱側面的導線），此磁力會對線圈造成力矩，我們知道 $$N$$ 匝線圈在磁場中所受的力矩為：

$$\tau = NIAB\sin\theta$$

其中 $$A$$ 為線圈所包覆的面積、$$B$$ 為徑向（平行鐵製圓柱半徑方向）的磁場、$$\theta$$ 為線圈法方向和 $$B$$ 的夾角。
Continue reading →

磁力（Magnetic Force）
台中縣立中港高級中學物理科王尊信老師/國立彰化師範大學物理學系洪連輝教授責任編輯

所謂的靜電力指的是將電荷放進電場中所受到的力，磁力亦是如此，若電荷在垂直的磁場中以速度v移動，也會受到磁力的影響而改變運動方式。

首先，我們討論載流導線在磁場中的受力情形。現有一個穿出紙面的均勻磁場，在磁場中我們放入一個長L、載有電流I(方向由右到左)的導線(如圖一)，發現導線受力作用而運動，受力方向如圖二所示。
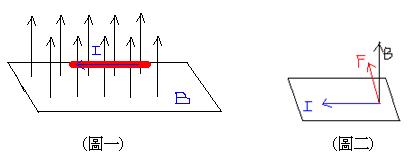Continue reading →

帶電粒子在磁場中的運動（Motion in a Magnetic Field）

先我們討論帶電粒子在磁場中的受力情形。假設有一個長L的導體，導體內部有n個帶有電量q的正電荷，若這些正電荷以速度v流過長L的導體，並花了時間t，我們可以知道，此時導體上的電流I為: 現在將此導體置入一個均勻磁場中，則此導體受到磁場的作用力為: 所以我們知道，一個帶電粒子所受到的磁力為: 帶電粒子在磁場中的運動基本上有三種，我們分別討論: 電荷移動的速度平行磁場:因為速度平行磁場，所以夾角θ=0˚或180˚，因此磁力為0，電荷不受磁場影響，繼續作等速度直線運動(假設沒受到其他外力)。
電荷移動的速度垂直磁場:速度垂直磁場，夾角θ=90˚或270˚，此時磁力為:F=qvb(方向垂直電荷的速度)，因此，原本作直線運動的電荷，受到這個法線力的影響，會開始作等速率圓周運動(因為把垂直的磁力視為向心力)。 電荷移動的速度和磁場夾θ角:因為夾θ角，所以速度平行磁場的分量會依然往前作等速度直線運動，而垂直磁場的分量會作等速率圓周運動，將兩個分量結合起來，則會發現，電荷在空間中作等速率螺旋運動(如下圖)。 分析上面的運動軌跡後，我們發現，帶電粒子在磁場中必作等速率運動。 在應用方面，科學家利用電荷速度垂直磁場會作等速率圓周運動的原理，製造了質譜儀，它可用來測量帶電粒子的質量和鑑別同位素，原理是將帶電粒子加速垂直射入磁場，此時 因此，若這些帶電粒子的質量不相等，迴旋半徑R的大小也會不同，藉此便可分離同位素了。
參考資料: http://en.wikipedia.org/wiki/Magnetic_field

帶電粒子在電場中的運動（Motion in an Electric Field）

  首先我們必須先知道帶電粒子在電場中的受力情形。

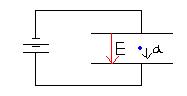
(圖一)

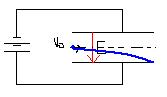
(圖二)
　　
在一個相距為D的兩平行金屬板上給予一個電位差V，則兩金屬平板會產生一個方向向下的靜電場E(圖一)，(假設忽略邊緣效應，即忽略平行板邊緣的非均勻電場所造成的影響)，其大小為: E=V/d。現在將一個質量為m、帶電量為q的正電荷放到電場中，則此電荷所受到的電力為: F=qE(向下)(因為電場方向等於電荷受力方向)，因此，我們知道F=qE(向下)=ma，將電場E帶入方程式，可以推得加速度a為: a=F/m=qE/m=qV/md (方向向下)。
　　

現在我們知道了帶電粒子在電場中的受力情形，藉此，我們便可討論帶電粒子在電場中的運動軌跡。
　　首先我們討論正電荷以初速度V₀平行電場移動的行為，因為初速度V₀平行電場，而正電荷在上述電場中會受到一個向下的加速度a，所以正電荷的運動軌跡會類似將物體垂直上拋(或下拋)，所受到重力加速度g的運動軌跡。
　　較值得討論的是，正電荷以初速度 垂直電場移動的行為(圖二)，現將座標原點設在正電荷的出發點，我們可以寫出運動方程式:

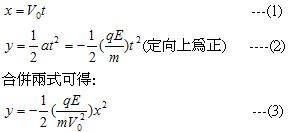
由此，我們可看出運動軌跡為一拋物線，這也類似於物體在重力場中的水平拋射軌跡，由式(3)中我們知道，y、x、E、V₀皆已知，由這個運動中我們可以發現電子的荷質比 (e/m)，再藉由米粒坎(Millikan)的油滴實驗得到了基本電量為: 16×10^-19庫倫，證明了電量量子化的概念。
　　在應用方面，湯木生也利用帶電粒子在電場和磁場中的運動原理設計了陰極射線管，後來的科學家將其發揚光大，設計了示波器，對於現在測量訊號週期、波形、相位等等數據，有了極大的便利。另外早期的電腦螢幕(CRT)、電視等等，也都是利用陰極射線管的原理所發明的。

參考資料: http://en.wikipedia.org/wiki/Electron