RC電路(RC circuit)

RC電路(RC circuit)
國立臺灣大學物理系 101級 劉仁宇

圖 1 最簡單的RC電路

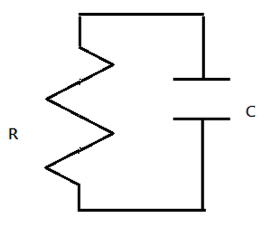
RC電路顧名思義是由電阻和電容所組成的電路，最簡單的形式如圖 1，該電容已經充電過，可視為一個電源供應器接上一個電阻，如果未充電過則儲存電荷量 $$Q$$ 為零，甚麼事也不會發生。

由於電路滿足克希何夫定律(Kirchhoff’s law)，亦即通過整個迴圈的總電位降為零，故可列式為

$$\displaystyle V=\frac{Q}{C}=IR$$

其中 $$V$$ 為電阻兩端的電壓，$$C$$ 為電容，$$Q$$ 為電容所儲存的電量。

又因為電容的電荷隨時間 $$t$$ 減少產生電流 $$\displaystyle-\frac{dQ}{dt}=I$$

聯立兩式可解得 $$\displaystyle \frac{dQ}{dt}=-\frac{1}{RC}Q$$，

分離變數後積分得 $$\displaystyle Q=Q_0e^{-\frac{t}{RC}}$$，其中 $$Q_0$$ 為一開始電容儲存的電荷量。

由上式可以知道電荷量會隨時間呈現指數遞減，

電流則是 $$\displaystyle I=-\frac{dQ}{dt}=\frac{Q_0}{RC}e^{-\frac{t}{RC}}$$也是隨著時間做指數遞減，

我們通常把電流遞減到起始值的 $$\frac{1}{e}$$ 倍所需時間稱做時間常數(time constant) $$\tau=RC$$。

圖2 含直流電壓的RC電路

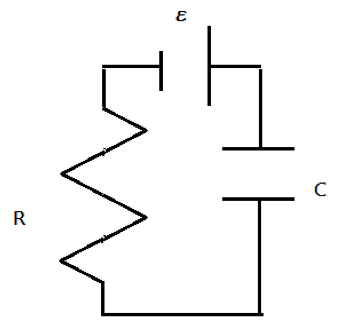
另一種常見的RC電路是加上一個定壓電源（電池）$$\epsilon$$，如圖 2。假設一開始電容未充電，依據克希何夫定律可得

$$\displaystyle\epsilon=\frac{Q}{C}+IR=\frac{Q}{C}+\dot{Q}R$$

上式為一階微分方程，可用分離變數法積分得

$$Q=\epsilon C(1-e^{-\frac{t}{RC}})$$

這表示電容所儲存電荷量從 $$0$$ 開始遞增，

直到經過無窮久後，電容才會充飽電 $$Q=\epsilon C$$，

而電流 $$\displaystyle I=\frac{dQ}{dt}=\frac{\epsilon}{R}e^{-\frac{t}{RC}}$$ 告訴我們電流隨時間做指數遞減直到電容充飽電。

電容本身可以儲存能量，其儲存功率是

$$\displaystyle P_C=d(\frac{Q^2}{2C})/dt=\frac{\epsilon^2}{R}(e^{-\frac{t}{RC}}-e^{-\frac{2t}{RC}})$$

再看電阻消耗的功率 $$\displaystyle P_R=I^2R=\frac{\epsilon^2}{R}e^{-\frac{2t}{RC}}$$，

而電池供應的功率 $$\displaystyle P=I\epsilon=\frac{\epsilon^2}{R}e^{-\frac{t}{RC}}$$

我們可以發現 $$P=P_C+P_R$$，亦即能量是守恆的。以力學系統來作比擬，電容本身僅將能量儲存，並不會耗散能量，這就像是力學系統中的保守力，而電阻則像是摩擦力一般，將供應的能量轉換成熱能耗散掉。

圖3 含交流電壓的RC電路

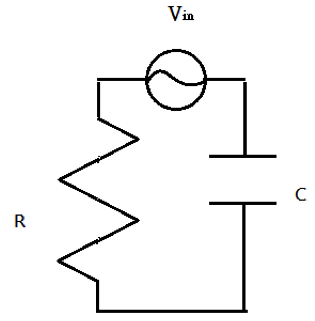
在現今蓬勃發展的積體電路，比較常見的是利用RC電路施加交流電做出低頻或高頻的濾波器，如圖 3。

首先討論低頻濾波器。只要輸入電壓是週期波，即使不是正弦波也可以透過傅立葉級數展開成正弦波的組合，所以可以單純假設輸入的交流電壓 $$V_{in}=V_0e^{i\omega t}$$ 為一正弦波，

取輸出電壓 $$V_{out}$$ 為電容兩端跨壓，

則 $$\displaystyle V_{out}=V_{in}\frac{1/i\omega C}{R+1/i\omega C}=V_{in}\frac{1}{1+i\omega RC}$$

上式中我們使用了電容的阻抗(impedance)為 $$1/i\omega C$$ ，

將兩端取絕對值可得 $$\displaystyle |V_{out}|=|V_{in}||\frac{1}{1+i\omega RC}|=V_0\frac{1}{\sqrt{1+\omega^2R^2C^2}}$$ ，

當角頻率 $$\omega$$ 很大時，$$|V_{out}|$$ 會變得很小甚至趨近於零，

反之，當角頻率 $$\omega$$ 很小時，$$|V_{out}|$$ 會很接近 $$V_0$$，

故此電路可將高頻的訊號濾掉，保留下低頻的訊號。

接下來是高頻濾波器，這次的輸出電壓 $$V_{out}$$ 為改成取電阻兩端跨壓，

則 $$\displaystyle V_{out}=V_{in}\frac{R}{R+1/i\omega C}=V_{in}\frac{1}{1+\frac{1}{i\omega RC}}$$

將兩端取絕對值可得 $$\displaystyle |V_{out}|=|V_{in}||\frac{1}{1+\frac{1}{i\omega RC}}|=V_0\frac{1}{\sqrt{1+1/\omega^2 R^2 C^2}}$$，

當角頻率 $$\omega$$ 很小時，$$|V_{out}|$$ 會變得很小甚至趨近於零，

反之，當角頻率$$\omega$$ 很大時，$$|V_{out}|$$ 會很接近 $$V_0$$，

故此電路可將低頻的訊號濾掉，保留下高頻的訊號。

高低頻的濾波器廣泛用於生活中的電器，如收音機接收訊號時必須選用適當的R和C值接收想要的訊號，並且可透過可變電阻或可變電容調整接收的頻率；麥克風中的放大器需要將適當的頻率範圍放大，捨棄掉高頻的雜訊和低頻的干擾。

RC電路在許多IC內也相當重要，比方說電晶體（BJT）、場效電晶體（MOSFET）的模型可簡化成較複雜的RC電路，而這兩個電路元件是製作電壓、電流、功率放大器，甚至是電流供應器不可或缺的重要元件。或許你會想說乾脆用RC電路就可以取代這些電路元件，但是在IC要求體積小的情況下RC電路就顯得相形見絀，因此我們仍需要這些電路元件，但是背後使用的原理是相同的。

參考文獻：

1. Sedra A. S.,Smith K. C.(2009), Microelectronics Circuits, Oxford University Press.
2. 2009年國際物理奧林匹亞競賽國家代表隊選訓教材第二冊（物理奧林匹亞國家代表隊選訓工作委員會）
3. 維基百科. RC circuit.  http://en.wikipedia.org/wiki/RC_circuit
4. 國立師範大學實驗教學物理實驗室. RC電路. http://www.phys.nthu.edu.tw/exphy/Download/ex15.pdf