泰勒多項式(2) (Taylor Polynomials(2))
泰勒多項式(2) (Taylor Polynomials(2))
臺北市立第一女子高級中學蘇俊鴻老師
連結:泰勒多項式(1) (Taylor Polynomials(1))
在〈泰勒多項式(1)〉中,我們提到:
任意實係數 \(n\) 次多項式 \(f(x)\),定能表成 \(f(x)\) 在 \(x=a\) 處的泰勒多項式
\(\begin{multline*}\displaystyle f\left( x \right) = f\left( a \right) + \frac{{f’\left( a \right)}}{{1!}}\left( {x – a} \right) + \frac{{f”\left( a \right)}}{{2!}}{\left( {x – a} \right)^2} + \frac{{f”’\left( a \right)}}{{3!}}{\left( {x – a} \right)^3} \\+\cdots+\frac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{\left( {x – a} \right)^n}\end{multline*}\)
這個定理對於我們回頭解決多項式的問題,或是研究多項式的性質很有幫助,本文的目的,就是提出泰勒多項式的幾個應用。
首先,透過泰勒多項式,下面這個問題就簡單多了。
\(f(x)=x^{20}+x^{10}+1\) 除以 \((x-1)^2\) 的餘式。
由 \(f(x)\) 在 \(x=1\) 處的泰勒多項式可知,
餘式為 \(f(1) + \frac{{f'(1)}}{{1!}}(x – 1) = 3 + 30(x – 1)=30x-27\)。
反之,我們也能掌握有關重根的條件。
比方說,若 \(x=a\) 為 \(f(x)\) 的二重根,
即 \(f(x)\) 被 \((x-a)^2\) 整除,則 \(f(a)=f'(a)=0\)(原因請讀者想想)。
因此,下列問題的多項式就很容易假設,
已知三次多項式 \(f(x)\) 滿足 \(f( – 1) = f(2) = f'(2) = 0\),\(f'(-1)=18\),求 \(f(x)\)。
由於 \(f( – 1) = f(2) = f'(2) = 0\),表示 \(f(x)\) 有 \((x+1)\) 及 \((x-2)^2\) 的因式。
故假設三次多項式 \(f(x)=a(x+1)(x-2)^2\)。
接著,
\(f'(x) = a{(x – 2)^2} + 2a(x + 1)(x – 2) \Rightarrow f'( – 1) = 9a =-18 \Rightarrow a=- 2\)。
因此,\(f'(x) = a{(x – 2)^2} + 2a(x + 1)(x – 2) \Rightarrow f'(-1)=9a =- 18 \Rightarrow a =- 2\)。
接下來,我們來看三次多項函數一個重要的性質:
三次多項函數圖形的對稱中心
實係數三次函數 \(f(x) = a{x^3} + b{x^2} + cx + d(a \ne 0)\) 為一點對稱圖形,
且以反曲點 \(( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\) 為圖形的對稱中心。
如何繪製三次多項函數的圖形,請參考本網站蘇惠玉老師〈三次函數圖形的繪製〉一文。
我們已經知道任意的三次函數 \(f(x)=ax^3+bx^2+cx+d\) 的圖形恰有一個反曲點 \(( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\)。上述性質則進一步表明反曲點 \(( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\) 同時也是圖形的對稱中心。也就是說,若點 \(P( – \frac{b}{{3a}} + k,f( – \frac{b}{{3a}} + k))\) 在 \(y=f(x)\) 的圖形上,那麼 \(P\) 以反曲點 \(( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\) 為對稱中心的對稱點 \(Q( – \frac{b}{{3a}} – k,f( – \frac{b}{{3a}} – k))\) 也會在 \(y=f(x)\) 的圖形上,如圖一所示。
由於 \(\displaystyle\frac{{( – \frac{b}{{3a}} + k) + ( – \frac{b}{{3a}} – k)}}{2} =- \frac{b}{{3a}},\forall k\),
只要能驗證 \(\displaystyle\frac{{f( – \frac{b}{{3a}} + k) + f( – \frac{b}{{3a}} – k)}}{2} = f( – \frac{b}{{3a}})\) 也成立,
那麼 \(( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\) 就是 \(\overline {PQ}\) 的中點,也就證明上述性質。
考慮 \(f(x)\) 在 \(x =-\frac{b}{{3a}}\) 處的泰勒多項式,得
\(\begin{multline*}\displaystyle f(x) = f( – \frac{b}{{3a}}) + \frac{{f'( – \frac{b}{{3a}})}}{{1!}}(x + \frac{b}{{3a}}) + \frac{{f”( – \frac{b}{{3a}})}}{{2!}}{(x + \frac{b}{{3a}})^2} \\\displaystyle+ \frac{{f”'( – \frac{b}{{3a}})}}{{3!}}{(x + \frac{b}{{3a}})^3}\end{multline*}\)
由於 \(( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\) 為反曲點,故 \(f”( – \frac{b}{{3a}}) = 0\)。
因此,\(\displaystyle f(x) = f( – \frac{b}{{3a}}) + \frac{{f'( – \frac{b}{{3a}})}}{{1!}}(x + \frac{b}{{3a}}) + \frac{{f”'( – \frac{b}{{3a}})}}{{3!}}{(x + \frac{b}{{3a}})^3}\)
接著,將 \(x =- \frac{b}{{3a}} + k\) 與 \(x =- \frac{b}{{3a}}- k\) 代入,得
\(f( – \frac{b}{{3a}} + k) = f( – \frac{b}{{3a}}) + \frac{{f'( – \frac{b}{{3a}})}}{{1!}}(k) + \frac{{f”'( – \frac{b}{{3a}})}}{{3!}}{(k)^3}\)
\(f( – \frac{b}{{3a}} – k) = f( – \frac{b}{{3a}}) + \frac{{f'( – \frac{b}{{3a}})}}{{1!}}( – k) + \frac{{f”'( – \frac{b}{{3a}})}}{{3!}}{( – k)^3}\)
兩式相加,可得
\(f( – \frac{b}{{3a}} + k) + f( – \frac{b}{{3a}} – k) = 2f( – \frac{b}{{3a}}) \Rightarrow \frac{{f( – \frac{b}{{3a}} + k) + f( – \frac{b}{{3a}} – k)}}{2} = f( – \frac{b}{{3a}})\)
因此,點 \(( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\) 是圖形的對稱中心。
其實,由上述三次函數 \(f(x)\) 在 \(x =- \frac{b}{{3a}}\) 處的泰勒多項式缺乏二次項的事實,
很容易就知道反曲點 \(( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\) 必為圖形的對稱中心。
事實上,知道函數圖形有對稱中心,有助於處理定積分和面積的關係。例如下面的問題,
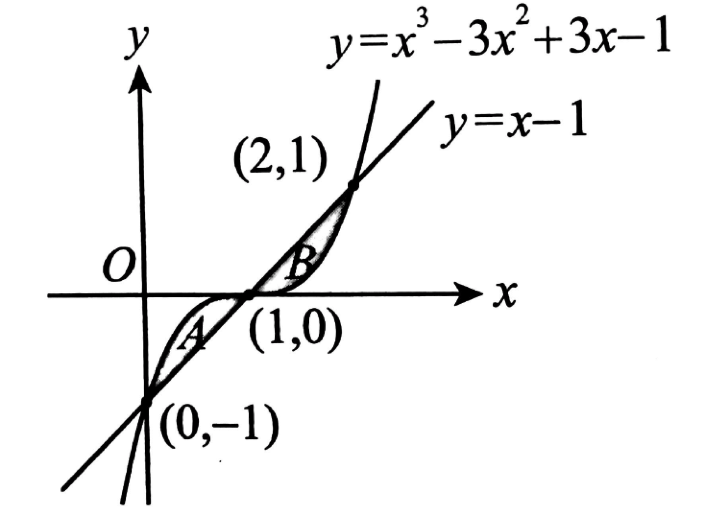
如圖二所示,已知兩圖形 \(y=x-1\) 與 \(y = {x^3} – 3{x^2} + 3x – 1\) 相交於三點,
並圍出兩塊封閉區域 \(A\) 與 \(B\)。試證:\(A\) 與 \(B\) 兩塊區域面積相等。
透過積分的計算,我們能夠證明 \(A\) 與 \(B\) 兩塊區域面積相等。
不過,若是觀察到點 \((1,0)\) 正是 \(y=x^3-3x^2+3x-1\) 的反曲點,那麼,由對稱性知道與兩塊區域面積必定相等也不失為一個好方法。可惜的是,這個性質並未列入高中數學課綱。
由上文來看,透過泰勒多項式的輔助,這個性質的證明並不困難呢!然而,上述所談種種泰勒多項式的應用,只是學習微積分的「小確幸」。事實上,布魯克.泰勒提出的泰勒定理(或稱為泰勒展開式),使得用多項式函數來「局部近似」任意函數的想法得以落實。因此,泰勒定理是微積分入門很重要的基本工具之一。有關泰勒定理的說明,請各位讀者自行參閱微積分書籍。
參考文獻:
- 蘇惠玉,〈三次函數圖形的繪製〉,/highscope/?p=47554


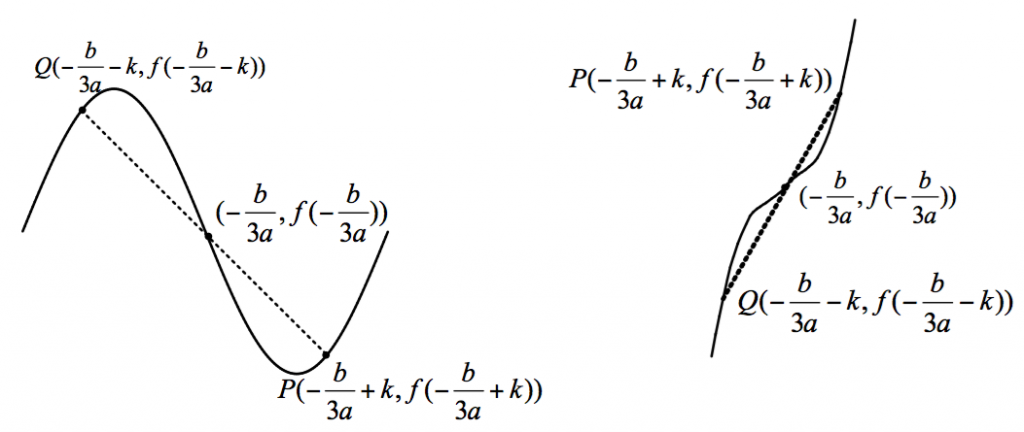
 前一篇文章
前一篇文章 下一篇文章
下一篇文章
