從牛頓的時代背景探索第二運動定律（下）
行政院科技部科技顧問／瑞典林雪平大學榮譽教授 趙光安
在伽利略和牛頓的時代，數學工具只有幾何、三角、和代數，物理知識也僅限日常生活中有系統的觀察，及少數的實驗結果。用現代的標準來衡量，伽利略和牛頓頂多只有國中畢業的程度。如果我們用現代的數理常識背景來解答三、四百年前的問題，那就是「事後有先見之明」了。雖然和「力學」有關的量測，伽利略得到的數據被推崇是權威性，然而他的「力學」實驗幾乎全部是基於物體的直線運動。在這個時代背景下，牛頓建立的理論，是從「一維系統」開始，然後才推廣到「三維空間」。因此，我們也從直線運動開始，試試看能否經歷一趟牛頓的思路。
泰勒多項式(2) （Taylor Polynomials(2)）
臺北市立第一女子高級中學蘇俊鴻老師
連結：泰勒多項式(1) （Taylor Polynomials(1)）
在〈泰勒多項式(1)〉中，我們提到：
任意實係數 \(n\) 次多項式 \(f(x)\)，定能表成 \(f(x)\) 在 \(x=a\) 處的泰勒多項式
\(\begin{multline*}\displaystyle f\left( x \right) = f\left( a \right) + \frac{{f’\left( a \right)}}{{1!}}\left( {x – a} \right) + \frac{{f”\left( a \right)}}{{2!}}{\left( {x – a} \right)^2} + \frac{{f”’\left( a \right)}}{{3!}}{\left( {x – a} \right)^3} \\+\cdots+\frac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{\left( {x – a} \right)^n}\end{multline*}\)
這個定理對於我們回頭解決多項式的問題，或是研究多項式的性質很有幫助，本文的目的，就是提出泰勒多項式的幾個應用。
泰勒多項式(1) （Taylor Polynomials(1)）
臺北市立第一女子高級中學蘇俊鴻老師
請考慮下面的問題：
已知多項式函數 \(f(x)=-x^3+5x^2-8x+4\)，求 \(f(0.99)\) 的值（四捨五入取到小數點以下第二位）。
儘管將 \(x=0.99\) 代入，即可求出函數值。
但 \(f(0.99) =- {(0.99)^3} + 5 \times {(0.99)^2} – 8 \times (0.99) + 4\) 繁複計算過程令人卻步。
因此，處理這類問題，通常採取下面的作法
以上題為例，由步驟一知，\(f(x) =- (x – 1) + 2{(x – 1)^2} – {(x – 1)^3}\)。所以，
\(\begin{array}{ll} f(0.99) &=-(0.99-1)+2\times{(0.99-1)^2}-{(1-0.99)^3}\\&=-(0.01)+2\times{(0.01)^2}-{(0.01)^3}\\&\approx -(0.01)=-0.01\end{array}\)
由步驟二的數值計算來看，應能推敲步驟一將原多項式改寫成以 \((x-1)\) 的冪次方升冪排列的多項式之用意。不過，進一步思考，上述解法正表明：當 \(1-\varepsilon\le x\le 1+\varepsilon\)，其中的 \(\varepsilon\) 為足夠小的正數時，有 \(f(x)\approx -(x-1)\)。
如何過圖形上一點求切線方程式(2)
（Finding an equation of the tangent line to the curve at the given point(2)）
臺北市立第一女子高級中學蘇俊鴻老師
接續〈如何過圖形上一點求切線方程式(1)〉最後提出的問題，本文的目的就是介紹微積分如何解決這些難題。首先，我們必須澄清什麼是切線？不能再像過去訴諸圖形直觀，需要對「切線」這個概念賦予明確的定義。我們想要在圖形上一點找到它的切線，因難之處在於我們需要相異兩點才能決定直線，如何能用「切點」定義呢？當然，微積分為我們解決這個困難。
切線的定義
如圖一，設 \(f(x)\) 為一函數，\(P(a,f(a))\) 是 \(y=f(x)\) 圖形上一定點。
在 \(P\) 點附近找圖形上異於 \(P\) 的一點 \(Q(x,f(x))\)，連接 \(P,Q\) 可得一割線 \(PQ\)。
當 \(Q\) 點沿著圖形以 \(Q_1,Q_2,\cdots\) 向 \(P\) 點趨近時，能得到一連串的割線 \(PQ_1,PQ_2,\cdots\)。
若 \(Q_n\) 沿著圖形趨近 \(P\) 時，割線 \(PQ_n\) 的極限直線 \(L\) 存在﹐
則稱直線 \(L\) 為 \(y=f(x)\) 圖形上過 \(P\) 點的切線﹐並稱 \(P\) 為切點。也就是說，
割線 \(PQ\xrightarrow{Q\rightarrow P}\)過 \(P\) 點的切線
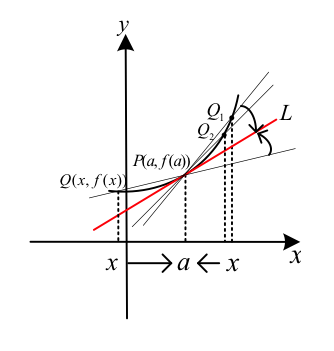
圖一
如何過圖形上一點求切線方程式(1)
（Finding an equation of the tangent line to the curve at the given point(1)）
臺北市立第一女子高級中學蘇俊鴻老師
給定一條曲線圖形(通常可視為函數圖形的一部份)，如何求出過圖形上一點的切線方程式？切線問題有著實際應用的對應。例如，運動物體在任意瞬間的運動方向，就是運動軌跡在那一點的切線方向。或是光學透鏡設計需要求出曲面的法線，而法線與切線垂直；若能求出切線，也就決定法線。
這些都是十七世紀當時科學研究和應用的一部份，這些需求促動微積分技術的發展，經過眾人的改進與演化，補強技術的理論，最終發展出微積分這一門優美又有威力的學問。靜心想想，討論「求切線方程式」問題一直是高中數學的主題之一，其解決方法的流變，頗有顯現此種數學知識積累的過程。因此，本文特意將高中數學中相關題材蒐集討論，以饗讀者。
