三次函數圖形的繪製
三次函數圖形的繪製
臺北市立西松高中蘇惠玉教師
當我們要描繪一個多項式函數圖形時,有幾個需要事先注意與處理的步驟:
- 確定自變數 \(x\) 的範圍;
- 求 \(y=f(x)\) 與座標軸的交點:
- 確定函數圖形是否有水平漸近線、鉛直漸近線或斜漸近線;
- 計算 \(f'(x)\),求出曲線上發生極值的點,同時也確定曲線的升降情況;
- 計算 \(f”(x)\),求出曲線上的反曲點,同時也確定曲線凹口向上或向下的情況。
接下來我們將就三次多項式函數的一階與二階導函數,一步步地討論與完成繪製三次函數的圖形。
三次函數圖形的特徵
設三次函數 \(f(x)=ax^3+bx^2+cd+d,~~a\ne 0\),
其 \(f'(x)=3ax^2+2bx+c\)、\(f”(x)=6ax+2b\)
\((1)\) \(f'(x)=0\) 有二相異實根
設實根為 \(\alpha\) 與 \(\beta\) (\(\alpha<\beta\)),
即可因式分解為 \(f'(x)=3a(x-\alpha)(x-\beta)\),\(f”(x)=3a(2x-\alpha-\beta)\)。
配合二次導函數與反曲點,當 \(a>0\) 時,可得與的函數值之正負變化情形,以及 \(y=f(x)\) 圖形的簡圖如下表:
\(a>0\):
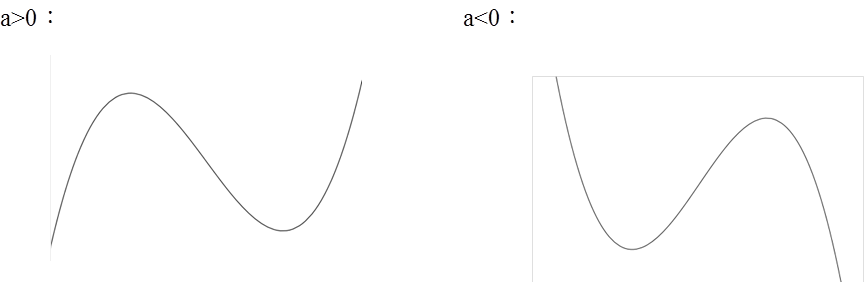
由上表可知,當 \(a>0\) 時,函數圖形為「右上升」;而當 \(a<0\) 時,所有遞增減的情形與凹口的情形皆與 \(a>0\) 時相反,且圖形為「右下降」。其圖形如下:
由圖形可知,此時三次函數有極值,極值點為 \((\alpha ,f(\alpha ))\) 、\((\beta ,f(\beta))\),利用這兩個點與 \(x\) 軸的相對位置,就可討論 \(f'(x)=0\) 的實根與虛根個數。
當 \(f'(\alpha)\cdot f'(\beta)<0\) 時,方程式有三相異實根;當 \(f'(\alpha)\cdot f'(\beta)=0\) 時,方程式有三實根(二重根與另一實根);當 \(f'(\alpha)\cdot f'(\beta)>0\) 時,方程式有二虛根與一實根。
\((2)\) \(f'(x)=0\) 只有一個實根
設實根為 \(\alpha\),亦即 \(f'(x)\) 可配方為 \(f'(x)=3a(x-\alpha)^2\),因此當 \(a>0\) 時,\(f'(x)\ge 0\),\(f(x)\) 為遞增函數;當 \(a<0\) 時,\(f'(x)\le 0\),\(f(x)\) 為遞減函數。
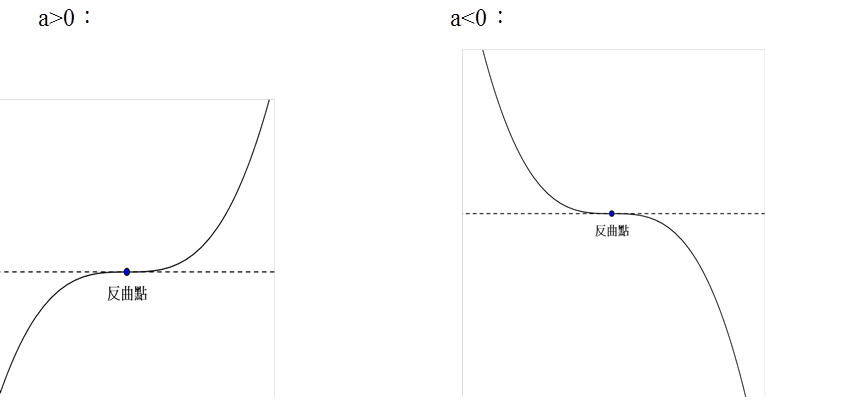
又 \(f”(x)=3a(x-\alpha)\),其反曲點為 \((\alpha,f(\alpha))\),但 \(f'(\alpha)=0\),亦即過反曲點 \((\alpha,f(\alpha))\) 可作一條水平切線。其圖形如下:
在此種情形下,再考慮 \(x\) 軸的位置,即可討論 \(f'(x)=0\) 的實根與虛根個數。
若反曲點 \((\alpha,f(\alpha))\) 在 \(x\) 軸上,即 \(f(\alpha)=0\),那麼方程式有三相等實根(為三重根);當 \(f(\alpha)\ne 0\) 時,方程式有二虛根與一實根。
\((3)\) \(f'(x)=0\) 沒有實根
即 \(f'(x)=3ax^2+2bx+c\) 之判別式 \(D<0\),因此當 \(a>0\) 時,\(f'(x)\) 恆正,亦即 \(f'(x)\) 為嚴格遞增函數;反之,當 \(a<0\) 時,\(f'(x)\) 恆負,亦即 \(f(x)\) 為嚴格遞減函數。
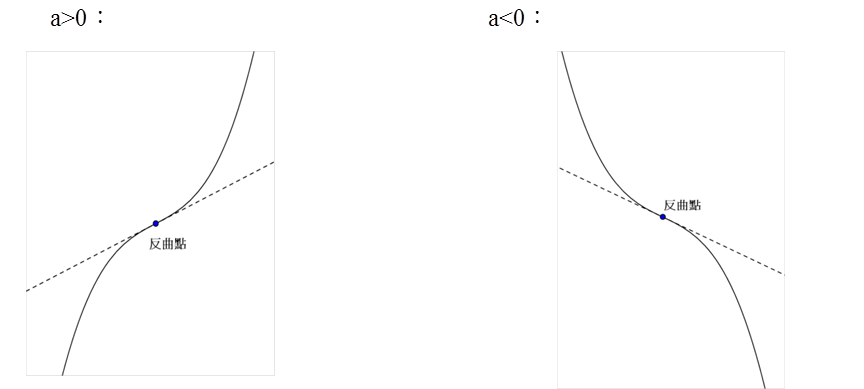
又反曲點為 \(\displaystyle( – \frac{b}{{3a}},f( – \frac{b}{{3a}}))\),且因為 \(f'(\displaystyle -\frac{b}{{3a}}) \ne 0\),因此在函數圖形在反曲點沒有水平切線。其圖形如下:
在這種情形下,無論 \(x\) 軸的位置為何,\(f(x)=0\) 的根都是二虛根一實根。


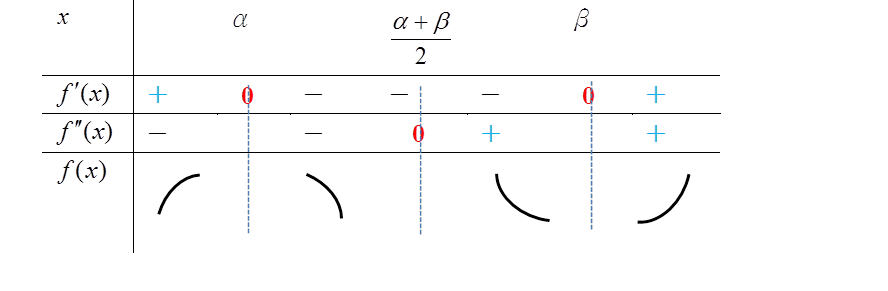
 前一篇文章
前一篇文章 下一篇文章
下一篇文章
