科氏力 (Coriolis force)
國立臺灣大學物理所黃一玄
在旋轉座標系(rotating reference frame)中，科氏力是使得物體偏移其運動方向的力，它使得在旋轉座標系上的觀察者，看到路徑呈弧線彎曲。如同離心力(centrifugal force)，科氏力是假想力的一種，但作用方向與離心力不同。離心力作用方向沿著圓周運動的半徑向外，科氏力是垂直於運動方向跟轉動軸方向(兩者外積之負方向)。
考慮在轉盤中心上跟著轉盤在轉動的人，她的手臂原來是向兩側垂直伸出的，之後手臂縮回身軀(或就如同芭蕾舞者的動作)，此時人的轉速會加快。注意到如果只看身軀的部分，則身體的質量並沒有改變，但轉速變快，這代表身體的角動量增大了，故身體一定受到一力矩使之加速。此力矩一定是由往身軀縮回的雙臂來提供，故雙臂在縮回的過程中必然受到某個力的作用，而且此力必與懸臂移動方向垂直。這個力正是科氏力。
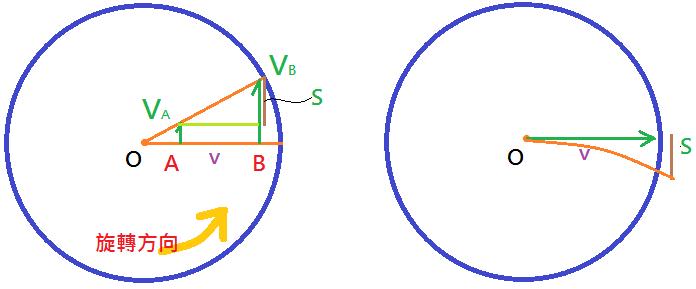
考慮在做圓周運動的轉盤(如圖一(a))，其中有 $$A$$、$$B$$ 兩點距離圓心距離分別是 $$r_A$$ 跟 $$r_B$$，速度分別是 $$v_A$$ 跟 $$v_B$$。現在有一人從 $$A$$ 點向 $$B$$ 快速擲出一球，球速度為 $$v$$。這顆球一開始除有向外(圖中向右)方向的速度 $$v$$ 以外，還有受到旋轉盤給的向北的速度 $$v_A=r_A\omega$$，而此時轉盤在 $$B$$ 點的速度為$$v_B=r_B\omega$$。由於 $$r_B>r_A$$，因此 $$v_B>v_A$$，也就是當球從 $$A$$ 到 $$B$$ 的時候，球往北的速度會低於 $$B$$ 點往北的速度，因此當球到達圓盤外緣時，球會落在 $$B$$ 點之後。
圖一：在做圓周運動的轉盤。(a) 左；(b) 右 (作者提供)
能階
國立臺灣大學物理研究所李培瑋
能階：指原子內電子所能存在的量子態；即電子只能在特定能量的軌道上運動，這些具有特定能量的軌道，稱為能階。
能階的概念，最早於1913年波耳(N. Bohr) 藉由探討氫原子光譜所提出的假設，其理論補足並修正了拉塞福(E. Rutherford)原子模型的缺失。
拉塞福原子模型
拉塞福(Rutherford)透過α-粒子(氦的原子核，He2+)撞擊薄金箔紙的實驗發現：大部份α-粒子會直接穿過，但仍有極少部分會以大角度反彈。因此推論原子的結構應該是：大部份質量、正電荷集中於中心的極小區域(原子核)，而原子核周圍則環繞著帶負電的電子。當然，科學家(包括拉塞福在內)都理解到此模型有著嚴重的問題。根據電磁學理論，帶電粒子做加速度運動的過程中會輻射出電磁波並因此失去能量。若電子繞著原子核做圓周運動，必會輻射出電磁波，導致電子能量漸減，繞核運動的半徑會愈來愈小，最終電子必墜毀於原子核(如圖一所示)。以氫原子為例，電子存在於氫原子的時間約為2×10-11秒，但這與原子的穩定存在不吻合。此外，拉塞福原子模型亦無法解釋原子光譜的不連續性。
速度
國立臺灣大學物理研究所楊淵棨
速度：
速度為非常基本的物理量之一，其對於描述物體的運動狀態尤其重要。速度為一種描述運動狀態的向量，所謂的向量，包含方向和大小，同樣的，速度也包含了速度的方向和速度的大小。物體速度的方向其實就是物體位移的方向，而其大小，就是量度位移快慢的一種量。速度可以依據所描述的狀態分為兩種：平均速度跟瞬時速度。
平均速度：
所謂平均速度，是用來描述物體在一段時間內的運動，它只跟開始的位置，結束的位置，以及總時間有關係。更具體說，假設 $$\vec{S_b}$$ 為結束的位置，$$t_b$$ 為結束的時刻，$$\vec{S_a}$$ 為開始的位置，$$t_a$$ 為結束的時刻，則平均速度 $$\vec{V}=\frac{\Delta\vec{S}}{\Delta t}$$ ，其中 $$\Delta\vec{S}=\vec{S_b}-\vec{S_a}$$ 為位移，$$\Delta t=t_b-t_a$$ 為總時間。也就是說，我們把物體這一段時間內的運動，表示成一個平均的等速度運動。
彈性常數 Spring Constant
國立臺灣大學物理研究所張翔恩
在中學甚至大學、研究所的物理課程中，老師似乎花了很多的時間與心力在教我們彈簧(Spring)的相關物理，為什麼呢?部分原因是由於彈簧是一個簡單的物體，但另一個很重要的原因則是：許多系統在些微偏離穩定平衡點時所受到的回復力常常可以利用彈簧來近似，因此我們可以用彈簧來模擬許多現象，幫助我們研究。
彈性力 Elastic Force
國立臺灣大學物理研究所張翔恩
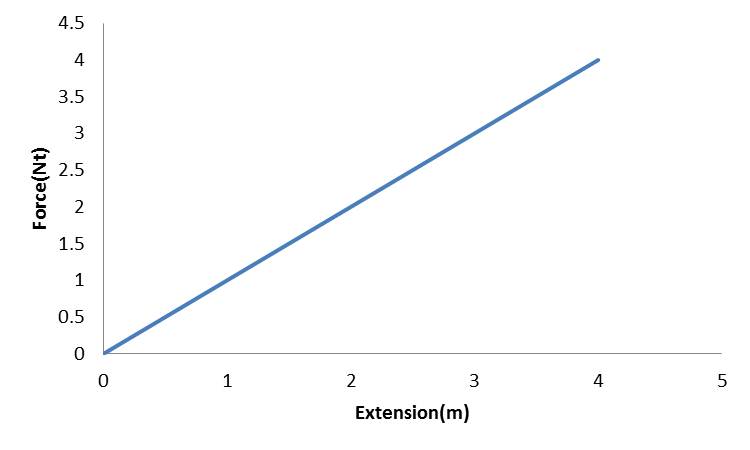
在介紹彈性力之前，我們先來說說甚麼是彈性(elasticity)。如果一個物體受到應力的作用而使其變形，過了一段時間，應力消失了，而該物體又恢復成原來的形狀，我們就稱該物體具有彈性。而讓該物體恢復原有形狀所需要的恢復力，就是彈性力。一般而言，當形變不是很大時，彈性力是遵守線性定律的，也就是說彈性力的大小會和造成物體形變的大小成比例關係(如圖一)。
圖一(作者提供)
傅科擺(Foucault pendulum)
國立臺灣大學物理所黃一玄
「這現象靜默的展現，既無形也永不停止。人們可以感覺到，可以看到它穩定的生成，它不受人為力量而加快或是減緩。看到這件事實的任何人都會駐足沉思、沉默片刻。而之後伴他離去的，則是那個對我們在太空中持續不間的運行有更敏銳體驗的永恆感覺。」
───傅科 (譯自Amir D. Aczel, Pendulum : Léon Foucault and the Triumph of Science, p xi, Atria Books (2004))
圖一照片來源：http://www.flickr.com/photos/iceninejon/289908913/sizes/l/in/photostream/
非慣性座標系 (Non-Inertial Reference Frame)
國立臺灣大學物理所黃一玄
若某一座標系相對於任一慣性座標系有加速度，則該座標系稱之為非慣性座標系。在非慣性座標系中，物理定律並非處在最簡單形式，特殊地，對於一個質量為 、受到外力為 $$F$$ 的質點來說，牛頓定律不再能單純地寫成 $$F=ma’$$ 的形式(其中 $$a’$$ 是非慣性座標系的觀察者所測到質點的加速度)。為了方便描述物體的運動，人們遂引入假想力的概念，令 F+F假想力 =ma’ ，使牛頓定律的形式得以成立。
雖然我們永遠可以選擇只採用慣性座標系來描述物體的運動，然而這並不總是處理問題最合適的方式。例如我們如果想了解受壓力梯度影響下的大氣移動，則因為我們是跟著地球在自轉，為了能非常直接而方便地應用到日常生活中，我們會選擇將計算的結果以隨著地球自轉的這個非慣性座標系來表示。
受激態(Excited State)
國立臺灣大學物理所羅雅琳
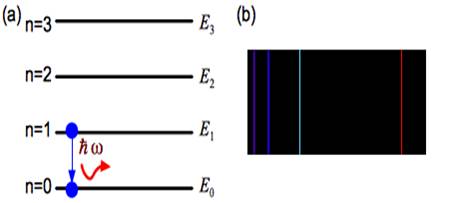
根據量子理論，一個系統的能量可能是離散的，而非如古典物理所述是連續的。我們把能量是離散的這個特性稱為能量的量子化(quantization)。該系統各個離散的能量所對應的狀態稱為一個能階(energy level)。我們通常可以用一組數字(稱為量子數，quantum number)去描述一個能階。當能量被量子化後，所有的量子態除了最低量子數所對應的基態（參見｢基態」條目）外，皆可稱之為受激態。如圖一 (a)所示，系統被量子化後，其各能階所對應的能量En 便是被量子數n所描述，而除了n=0的最低能量態外，其他所對應的量子態便是所謂的受激態。
圖一、(a)量子化能階圖。在量子化的圖像下，被描述的物理量與古典的連續量不同，取而代之的是用離散的量子數n來描述之，而En是用來描述量子化後能量。藍色表示粒子由受激態放出特定能量ℏω的光子回到基態。(b)氫原子發射譜線。（作者提供）
