干涉 (interference)
國立臺灣大學物理博士班嚴治平
在介紹干涉 (interference)之前，先介紹相位 (phase)與疊加原理 (superposition principle)！相位是波 (wave)最重要的性質之一，而疊加原理則是處理數個波在時間、空間上重疊時的方法。
先以一維的繩波來介紹：
在同一條繩子上有兩個繩波相向而行（參見圖一），當兩波交會時，在交會處繩子的振動方式乍看之下似乎有點複雜，但其實並不然，因為只需把向左傳播的繩波跟向右傳播的繩波在相同位置的振動相加便可，這就是疊加原理。不論有幾個波重疊在相同的時間、空間，將各自的振動相加就可以得到總和的波。 當不同的波在空間的某處疊加在一起時，我們便說這些波在進行干涉。
杯中茶葉何去何從？
國立臺灣大學物理學系陳義裕教授
這篇短文想要討論的是一個很易發現的現象：以一根湯匙去攪拌一杯泡有一點茶葉的茶水，則最後杯中的茶葉都會集中、聚集在杯底中央。為什麼？
一、以實驗室靜止觀察者的觀點看問題
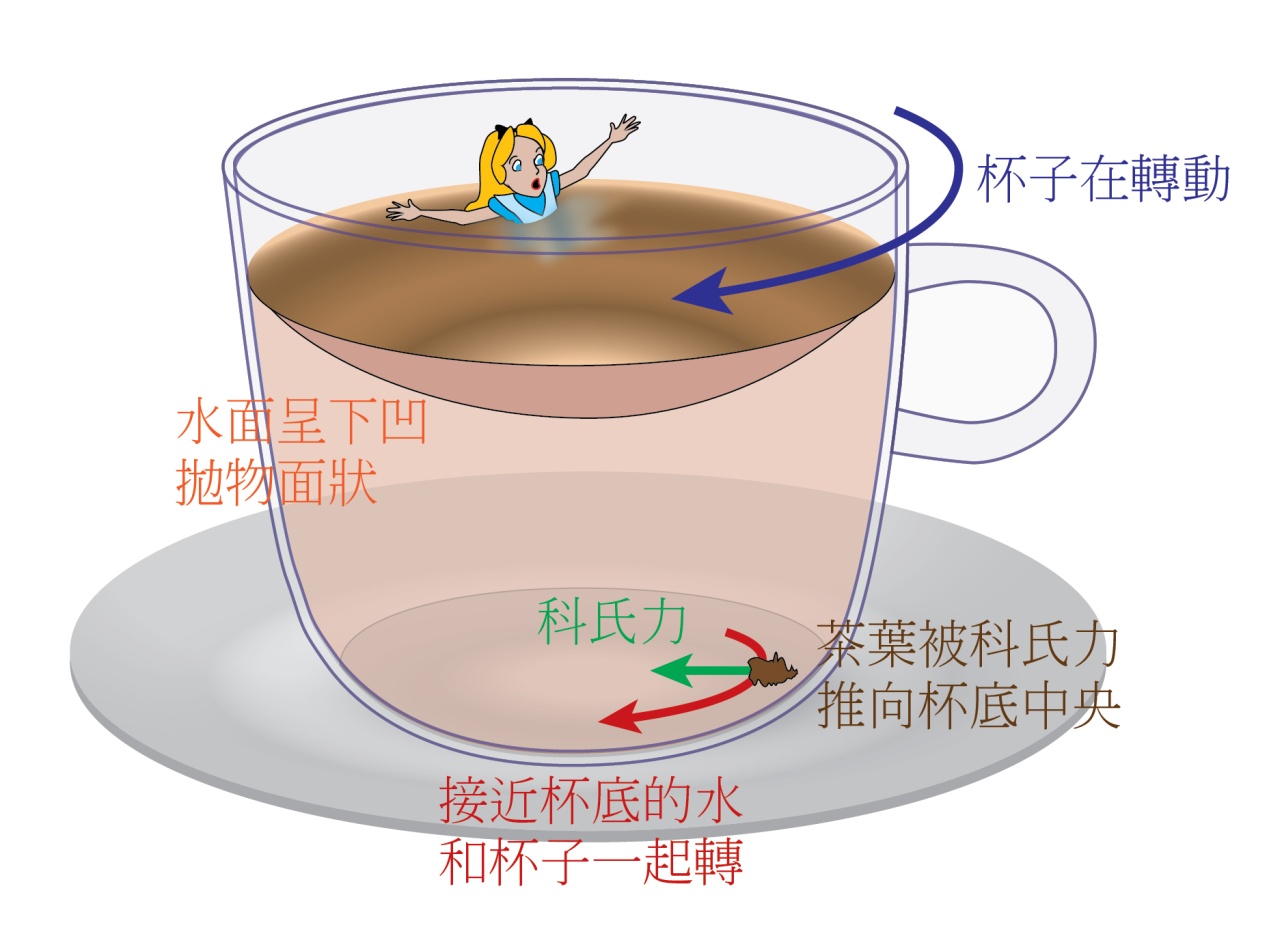
當你用一根湯匙去攪拌一杯水後，杯子中的水會整體轉動起來。如果當初攪拌的時候很使勁，杯子中的水轉動得特別快，我們還會發現水面中心明顯凹陷了下去，而靠近邊緣的水位則比較高，整個水面看起來就像是一個碟形天線的形狀(如圖一所示)。不用懷疑，此時水面與碟形天線的形狀真的是同一個模樣，我們將之稱為拋物面。
圖一 水在杯子中轉動，其水面呈下凹狀，與碟形天線的形狀同一個模樣，稱為拋物面。(為了展示效果，此圖故意將表面凹陷的情況誇大) (作者提供)
為什麼轉動中水的表面會呈中心凹陷的拋物面狀？這就要從水要如何去維持轉動的狀態說起。我們知道物體若要做等速圓周運動，則便需要一個向心力，杯子中的一個小水塊既然是在繞著杯子的中心軸轉動，自然也需要有向心力，而此向心力的來源，是由小水塊沿著徑向上的內外兩側之水壓大小不等來提供(如圖二所示)。
圖二 轉動中的小水塊沿著徑向上的內外兩側之水壓大小不等，這提供了小水塊做等速圓周運動所需要的向心力。(作者提供)
可是水壓在徑向上怎麼會出現內低外高的現象呢？原來水面之所以會呈現拋物面狀的祕密就在這裡了：我們在水中某個位置處之所以會感受到水壓，其實是因為它上方所有的水之重量累積疊加後壓了下來所致，因此只要其正上方之水面越高，則水壓就越大。從圖二我們可以看出，有了拋物面狀的水面，則在同一個高度處沿著徑向往外走出去時，其正上方水的深度一定是越來越大，所以水壓的分布一定是越往外就越大。
雖然杯中的水整體轉動得很一致(幾乎就像是一個圓柱體在繞著其中心軸旋轉一般)，但是接近杯底的水就沒辦法轉那麼快了，原因是日常生活中所接觸到的流體都有一個很有趣的特性：和固體接觸的流體很喜歡附著、緊貼著固體表面；它會賴在那裏不想流走。由於杯子是靜止不動的，杯底當然就沒有在轉動，所以接近杯底的水就處於一種很尷尬的場面：一方面在它正上方有一大團轉動得非常快的水想要帶著它一起轉動，但另一方面它又因為貼著杯底，事實上是不太能夠動的，所以做個妥協，接近底部的水就只好慢慢地轉，如圖三動畫所示。
假想力(fictitious force, also pseudo force, inertial force(慣性力))
國立臺灣大學物理所黃一玄
以非慣性座標系描述運動時，物體並不遵守牛頓運動定律。為了使牛頓運動定律看起來仍能成立，我們只好多引入假想力的概念，此假想力完全不是因為物體間有實質的交互作用而產生。在旋轉座標系中，假想力包含離心力跟科氏力。
例一：
假想坐在轎車中的乘客，於汽車突然啟動時，乘客感覺到身體似乎被向後拋、背部跟著緊貼住座椅；而當行車驟然停止時，乘客感受到一個往前的衝力；急轉彎時，身體則會側向往轉彎外側拋甩。
例二：
如圖一，想像你是愛莉絲，吃了縮小蘑菇之後掉入瘋子哈特(Mad Hatter)攪拌中的茶杯，你跟水流方向同步，被水流帶著走，你會看到身旁的水是靜止的，而整個杯子則是反向旋轉。在接近底部的地方，水有跟著杯底一起運動的特性，所以對愛莉絲來說，這些水有一個圓周運動的速度。伴隨著這個速度的科氏力會指向杯子中央，於是茶葉順著水流被推向杯底中央聚集起來。此外，愛莉絲還會發現水面不是平的，而是呈外高內低的拋物面狀，這是因為對她來說周遭的水會感受到離心力，而將水往外拋去，結果外緣就會累積較高的水位。
圖一 愛莉絲被水流帶著走，她會看到身旁的水是靜止的，但整個杯子則是反向旋轉。 (陳義裕繪)
離心力 (Centrifugal force)
國立臺灣大學物理所黃一玄
在旋轉座標系中(rotating reference frame)，不論一物體相對於該觀察者是靜止的或是在運動，對此觀察者來說，物體都會感受到一沿轉動半徑向外推出(或拉出)的力，此力稱為離心力。它是由於旋轉觀察者不斷在改變其座標軸的方向下所呈現出來的效果。
考慮旋轉一個水桶，水桶綁上一根繩子，水桶裡面裝水，而當開始晃動水桶進而轉動的時候，此時手拉住繩子的力是向心力的來源，由於此向心力不斷改變水桶的速度方向，因此對於一位與水桶維持同步轉動的觀察者來說，水桶本身會因為自身慣性感受到向外甩出的力，此便是離心力。若繩子鬆脫，手不再對水桶施力，對於任何一個仍維持著轉動的觀察者而言，他仍然會觀察到水桶對他來說受到一個離心力。因此，離心力並不是由於有一個實體的作用力去使物體轉動，結果物體才因應出一個離心力。
現在考慮水桶裡面的水，當水桶的速度到達某一臨界速度之後，速度夠快可以使水桶經過施力者的頭頂完整的繞一周，此時這個看似把水桶中的水固定在水桶底部， 使施力者不會變成落湯雞的離心力，實際上是由於水桶本身不斷擠壓水，使水改變方向來維持圓周運動所導致，意思是：是水桶推著水走，而不是水被桶底吸住。假如我們擺一個測重計在桶底，則可以測到這個由於不斷改變速度方向造成的加速度(及作用力)的量值。
相對論性質量(Transverse and Longitudinal Mass)
國立臺灣大學物理研究所徐銘鍵
自從愛因斯坦發現狹義相對論之後，人們了解到質量和能量有緊密的關係，著名的質能互換公式(mass-energy equivalence)為
$$E=\sqrt{(m_0c^2)^2+(pc)^2}\equiv mc^2$$
其中 $$p$$ 是物體的動量，$$c$$ 是光速，$$m_0$$ 是靜止質量(rest mass; 也是一般人所熟知的質量)，$$m$$ 稱為相對論性質量(relativistic mass)，它可以說是直接從能量 $$E$$ 除以定義 $$c^2$$ 而來。
迴旋頻率 (cyclotron frequency)
國立臺灣大學天文物理研究所吳志恆
當帶電粒子相對磁場運動時，粒子會受到勞侖茲力(Lorentz force)的作用，又因為勞侖茲力為 $$\vec{F}=q\vec{v}\times \vec{B}$$，所以勞侖茲力的方向與速度的方向垂直。所以，自由帶電的粒子在均勻的磁場中運動時，因為勞侖茲力的方向與速度的方向垂直，所以磁場不會對粒子作功，因此粒子的速率不變。因為粒子的速率不變，根據牛頓第二定律，當物體初速度與磁力是垂直的時候，它受到此量值為恆定的力，則運動軌跡的曲率不變，所以物體在作圓周運動。
馬力(Horse power)
國立師範大學物理系博士後研究員胡耿銘
定義
馬力是功率的單位，又俗稱為“匹”，源自英語 $$\bf{horse~power}$$ 翻譯而來，概念上是指一匹馬所做功的功率。而一般最常見被提到的馬力定義上有兩種，英制馬力與公制馬力。
力學能( Mechanical energy)
國立臺灣大學物理系簡嘉泓
定義
或譯為機械能，為動能與位能的總和，位能即常見之重力位能、電力位能及彈性位能等保守力造成之位能，其單位為焦耳$$(J)$$，且僅有大小而無方向，若一物體含有越多的位能則代表它能夠對其他物體做越多功(work)。
力學能守恆
力學能的定義為位能 $$U$$ 與動能 $$E_k$$ 之總和，即 $$E_{mechanical}=U+E_k$$
動能與位置無關，僅與物體之質量 $$m$$ 與速度 $$v$$ 有關，定義為 $$E_k=\displaystyle\frac{1}{2}mv^2$$
位能僅與物體在保守力場中之位置有關，從 $$\vec{x_1}$$ 移動到 $$\vec{x_2}$$ 的位能變化可表示為
$$\displaystyle \Delta U=-\int_{\vec{x_1}}^{\vec{x_2}} \vec{F}\cdot\mathrm{d}\vec{x}$$
$$\vec{F}$$ 為物體在力場中所受的力。位能為一相對量，所以必須選定一參考位置做為基準。所謂力學能守恆，是一系統若不受外力作功(即無能量進出該系統，包含其內部的化學反應)，其內部的動能與位能總合會維持不變。常見系統如理想上之彈簧系統、自由落體、單擺等。
阿特午機 Atwood’s machine (也常譯作阿特午德機)
國立臺灣大學物理系林司牧
阿特午（George Atwood ，1745年10月-1807年7月11日）是英格蘭數學家、西洋棋棋手。他在 1784 年發表的《關於物體的直線運動和轉動》一文中提出一種用於測量加速度及驗證運動定律的機械，後世稱之為阿特午機。一個最簡單的理想阿特午機如圖一所示，其繩子視為無重量、無彈性，理想滑輪無重量且無摩擦力。