奇函數與偶函數

奇函數與偶函數 (Odd Functions and Even Functions)
國立台南第一高級中學數學科林倉億老師/國立臺灣師範大學數學系許志農教授責任編輯

摘要:本文說明何謂「奇函數」與「偶函數」，以及其圖形之特性：奇函數圖形會對稱原點，而偶函數的圖形會對稱 軸。另外還簡要介紹奇函數與偶函數的一些性質。

何謂「奇函數」？對定義域內每個 \(x\)，函數 \(f(x)\) 恆有 \(f(-x)=-f(x)\) ，則稱 \(f(x)\) 為奇函數。

在多項式函數中，只要是奇數次的單項次函數如 \(f(x)=x\)、\(f(x)=x^3\)、\(f(x)=x^{2k-1}(k\in N)\) 統統都是奇函數。

更進一步地，一個多項式函數中的每一項若都是奇數次，例如

\(f(x)=a_{2k-1}x^{2k-1}+a_{2k-3}x^{2k-3}+\cdots+a_1x,~~~k\in\mathbb{N}\)

，由定義可得

\(\begin{array}{ll}f(-x)&=a_{2k-1}(-x)^{2k-1}+a_{2k-3}(-x)^{2k-3}+……+a_1(-x) \\&= -(a_{2k-1}x^{2k-1}+a_{2k-3}x^{2k-3}+……+a_1x)\end{array}\)

，即得 \(f(x)\) 是奇函數。

至於「偶函數」，就是對定義域內每個 \(f(x)\)，函數 \(f(x)\) 恆有 \(f(-x)=f(x)\) 時，就稱 \(f(x)\) 為偶函數。

在多項式函數中，只要是偶數次的單項次函數以及常數函數如 \(f(x)=1\)、\(f(x)=x^2\)、\(f(x)=x^{2k} (k\in N)\) 統統都是偶函數。仿照奇函數的推論可以知道，一個多項式函數中的每一項若都是偶數次或是常數項，則這個函數就會是偶函數。

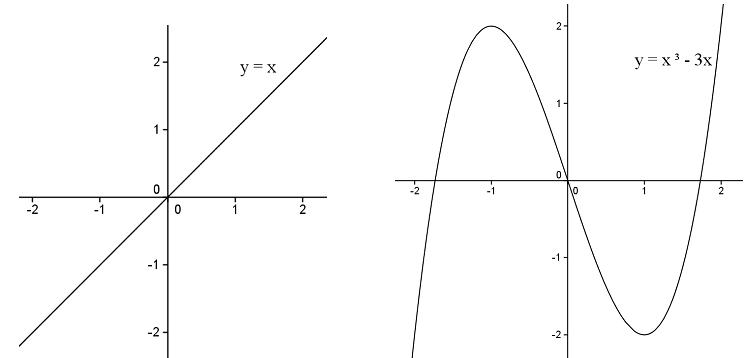
從上述的定義，我們還可以推知奇函數與偶函數圖形的特徵。先看奇函數，若點 \((a,b)\) 在 \(f(x)\) 的圖形上，即 \(f(a)=b\)，從定義可得知 \(f(-a)=-f(a)=-b\)，所以點 \((-a,-b)\) 也會在圖形上。也就是說，奇函數 \(f(x)\) 的圖形會對稱原點。如下圖幾個例子：

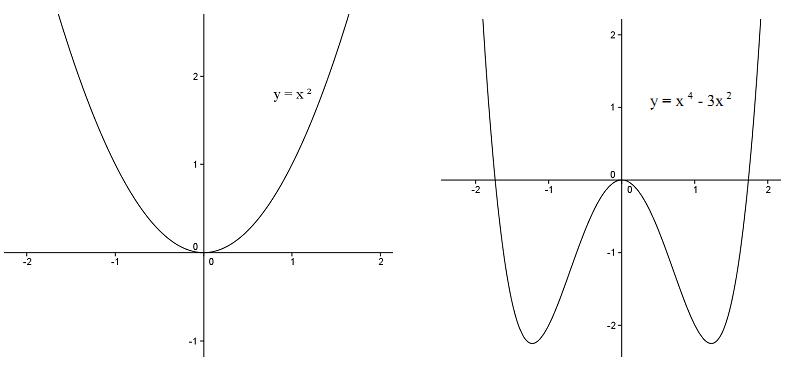
至於偶函數，若 \((a,b)\) 在 \(f(x)\) 的圖形上，即 \(f(a)=b\)，從定義可得知 \(f(-a)=f(a)=b\)，所以點 \((-a,b)\) 也會在圖形上。也就是說，偶函數 \(f(x)\) 的圖形會對稱原點。如下圖幾個例子：

有了奇函數與偶函數的定義之後，我們還可以進一步得到：「任何一個函數 \(f(x)\) 一定可以寫成一個奇函數與一個偶函數的和。」這個性質就比較不那麼直觀了，但仔細觀察下列兩個函數：

\(\displaystyle g(x)=\frac{f(x)-f(-x)}{2}\)、\(\displaystyle h(x)=\frac{f(x)+f(-x)}{2}\)

，可以發現 \(g(x)\) 正是一個奇函數，\(h(x)\) 正是一個偶函數，而 \(g(x)+h(x)=f(x)\)。

原來要將一個函數分解成奇函數與偶函數的和，不需要從茫茫「函數」海中去找，從 \(f(x)\) 反求諸己就可以找到答案了。有興趣的讀者還可以嘗試證明，這種分解方式是唯一的。

奇函數與偶函數還有許多其他的性質，在此僅列出可以用多項式函數理解、驗證的性質，供讀者自行驗證：

1. 奇函數乘以一個常數後，仍然是奇函數。偶函數亦同。
2. 奇函數加奇函數，仍然是奇函數。偶函數亦同。
3. 奇函數乘以奇函數會成為偶函數，而偶函數乘以偶函數仍會是偶函數。
4. 兩個奇函數合成後，仍然是奇函數。偶函數亦同。
5. 一個奇函數與一個偶函數的合成，會成為偶函數。

參考資料

1. 林福來等  (2011)，《普通高級中學數學第一冊》，南一書局。
2. http://zh.wikipedia.org/wiki/%E5%A5%87%E5%87%BD%E6%95%B8