地位量數（下）—中位數、眾數

Posted on 2016/08/18 in 數學, 數據分析, 機率統計 with 尚無留言 7,399 views

地位量數（下）—中位數、眾數 (Measures of Location (II)： Median, Mode)
國立成功大學統計系藍翊文

本篇接續介紹中位數及眾數兩種地位量數。中位數與眾數均不受太大或太小的觀測值（又稱極端值）影響，因此又稱為穩健 (robust) 地位量數。

1. 中位數 (median)：將資料由小排到大，找出位於中間項的數值（當樣本數個數為奇數）或中間兩項之平均值（樣本數個數為偶數），舉例來說，有 \(n\) 筆資料由小排到大，排名第 \(k\) 的資料記為 \(x_{(k)}\)，可得 \(x_{(1)}\le x_{(2)}\le … \le x_{(n)}\)，則中位數為：

\(M=\left\{\begin{array}{ll}x_{(\frac{n+1}{2})} & \text{, if } n \text{ is an odd number} \\\frac{1}{2}[x_{(\frac{n}{2})}+x_{(\frac{n+2}{2})}] & \text{,if } n \text{ is an even number} \\\end{array}\right.\)

例： \(15\) 位打靶者，每人有 \(13\) 發子彈，其中靶的次數如下：

\(13, 1, 5, 6, 7, 8, 4, 5, 6, 7, 8, 11, 12, 6, 8\)

求 \(15\) 位同學中靶次數的中位數。

解：將 \(15\) 位同學中靶次數由小至大排序結果如下

\(1, 4, 5, 5, 6, 6, 6, 7, 7, 8, 8, 8, 11, 12, 13\)

由於樣本大小 \(n = 15\) 為奇數，中位數為排名第 \((15+1) / 2 = 8\) 的數值，\(x_{(8)}=7=M\)。

若欲計算已分組資料的中位數，且假設各組次數均勻的分布在該組內時，則中位數計算公式為

\(\displaystyle M=L_M+\left(\frac{n}{2}-F_{L_M}\right)\times \frac{h_M}{f_M}\)

\(L_M\)：中位數所在的組之下界
\(F_{L_M}\)：累積至 \(L_M\) 的個數
\(h_M\)：中位數所在組的組距
\(f_M\)：中位數所在組的個數。

例：表三為已分為五組之樣本，樣本大小為 \(30\)，可知中位數的位置在由小排到大之第 \(15\) 及第 \(16\) 數字中間，將次數累加可知，中位數會落在 69.5-79.5 那組，因此

\(\displaystyle M=L_M+\left(\frac{n}{2}-F_{L_M}\right)\times \frac{h_M}{f_M}=69.5+(\frac{30}{2}-8)\times\frac{10}{12}=75.33\)

表三、已分組資料中位數計算範例。（本文作者藍翊文製）

組界	組中點 (x) （自行計算）	次數 (f)	組中點\(\times\)次數（自行計算）
49.5-59.5	54.5	2	109
59.5-69.5	64.5	6	387
69.5-79.5	74.5	12	894
79.5-89.5	84.5	7	591.5
89.5-99.5	94.5	3	283.5
		30	2265

2. 眾數 (mode) 的定義為資料當中出現頻率最多的數值，因此，眾數不一定唯一（可以有多個）。

A. 未分組資料

例：一班級進行投籃比賽，派出 \(10\) 位同學，每人投 \(10\) 個球，進球數如下，求眾數。

\(4, 4, 7, 5, 2, 7, 8, 7, 4, 3\)

解：計算進球數出現的頻率分別如下表：

表四、進球數頻率表。（本文作者藍翊文製）

進球數	2	3	4	5	7	8
頻率	1	1	3	1	3	1

由於進球數 \(4\) 和 \(7\) 次出現次數最多、均為 \(3\) 次，因此此筆資料之眾數為 \(4\) 及 \(7\)。

B. 已分組資料：遇到分組資料欲求眾數 \((M_0)\) 有以下幾個方法：

金氏法 (King’s method)

\(\displaystyle M_0=L_{M_0}+\frac{f_{+1}}{f_{+1}+f_{-1}}\times h_{M_0}\)

\(L_{M_0}\)：眾數（次數最多的組）所在組的下界
\(f_{+1}\)：眾數所在組之下一組的個數
\(f_{-1}\)：眾數所在組之前一組的個數
\(h_{M_0}\)：眾數所在組的組距。

克氏法 (Czuber’s method)

\(\displaystyle M_0=L_{M_0}+\frac{f_{M_0}-f_{-1}}{(f_{M_0}-f_{+1})+(f_{M_0}-f_{-1})}\times h_{M_0}\)

\(L_{M_0}\)：眾數（次數最多的組）所在組的下界
\(f_{+1}\)：眾數所在組之下一組的個數
\(f_{-1}\)：眾數所在組之前一組的個數
\(f_{M_0}\)：眾數所在組的個數
\(h_{M_0}\)：眾數所在組的組距。

皮爾森法 (Pearson’s method)

其法是使用平均數、中位數及眾數之關係所推導：

\(M_0=\overline{x}-3(\overline{x}-M)\)

\(\overline{x}:\) 平均數，\(M:\) 中位數，\(M_0:\) 眾數

例：現有一組已分組資料，記錄如下，使用金氏法、克氏法、皮爾森法分別求出眾數。

表五、已分組資料眾數計算範例。（本文作者藍翊文製）

組界	次數
29.5-39.5	3
39.5-49.5	3
49.5-59.5	10
59.5-69.5	5
69.5-79.5	4
79.5-89.5	5

解：由上表可知，眾數落在 49.5-59.5 這組。

金氏法：\(\displaystyle M_0=49.5+\frac{5}{5+3}\times 10=55.75\)

克式法：\(\displaystyle M_0=49.5+\frac{10-3}{(10-5)+(10-3)}\times 10=55.33\)

皮爾森法：\(M_0=\overline{x}-3(\overline{x}-M)\)

\(\displaystyle\overline{x}=\frac{34.5\times 3+44.5\times 3+…+84.5\times 5}{2+3+…+6}=\frac{1825}{30}=60.833\)

\(M=49.5+(\frac{30}{2}-6)\times\frac{10}{10}=58.5\)

\(M_0=60.833-3(60.833-58.5)=53.834\)

3. 三種主要地位量數之間的關係

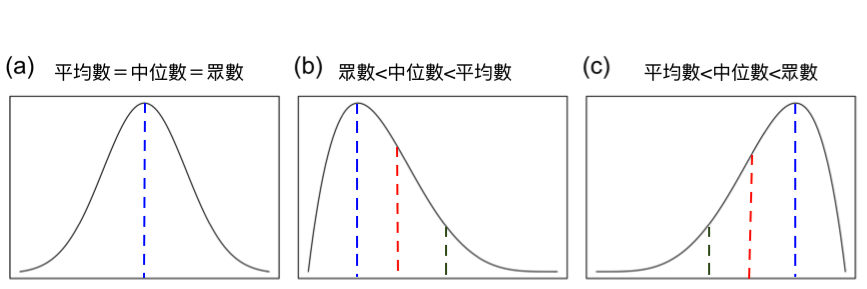
平均數、中位數與眾數等三種主要應用的地位量數之大小關係，依據樣本的資料型態而定。假設樣本均為單模 (single modal) 的形態（即樣本的眾數發生的位置僅有一處，若以直方圖 (histogram) 呈現數據，僅有一處高峰），則三種地位量數的大小關係與資料的偏態 (skewness) 有關（圖一）。若資料呈左右對稱的分佈，則平均數、中位數與眾數約略相等。若資料呈右偏（正偏）分布，亦即有少數幾個偏大的數據，則平均數 > 中位數 > 眾數。若資料呈左偏（負偏）分布，亦即有少數幾個偏小的數據，則平均數 < 中位數 < 眾數。