三次方根與三角函數
三次方根與三角函數 (Cubic Roots and Trigonometric Functions)
臺北市立大直高級中學數學科高子婷老師/國立臺灣大學數學系翁秉仁教授責任編輯
摘要:解三次方程式用卡當公式,卡當公式需開複數的立方根,開複數立方根可用棣美弗定理,棣美弗定理又和三角函數脫不了關係,換言之即使低次如三次方程式也和三角函數密切相關,本篇文章就上述幾者的關係做個討論。
棣美弗定理與複數方根
棣美弗最有名的定理,就是高中課本裡的「棣美弗定理」:
$$(\cos\theta+i\sin\theta)^n=\cos n\theta+i\sin n\theta$$
※ 此公式棣美弗證明了 $$n$$ 為自然數時成立,1749年時尤拉則證明了 $$n$$ 為實數也成立。
在高中學習棣美弗定理最主要能幫助我們找複數的方根。
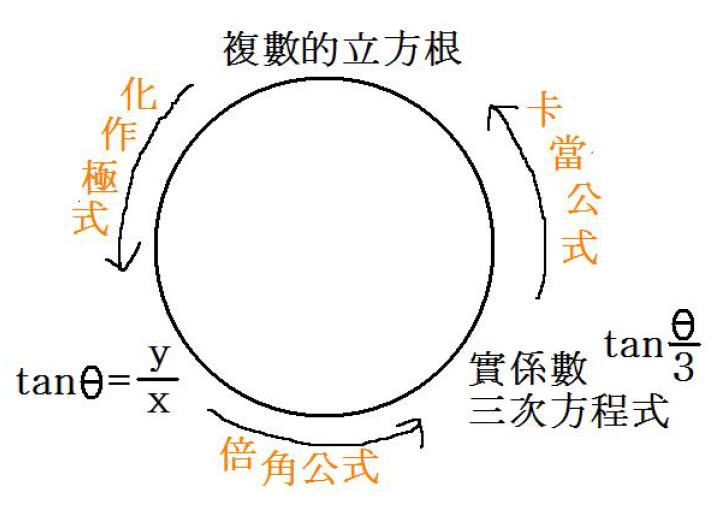
以三次方根為例,欲解 $$z^{3} =x+yi$$,其中 $$x,y\in\mathbb{R}$$,首先將 $$x+yi$$ 表示成複數的極式,即
$$x+yi=r(\cos\theta+i\sin\theta)$$ 其中 $$r=\sqrt{x^2+y^2},~\theta=\tan^{-1}\frac{y}{x}$$
將之代回,比較兩邊極式的幅角與絕對值,即可解得
$$\displaystyle z=\sqrt[3]{r}\left(\cos(\frac{\theta}{3}+120^\circ k)+i\sin(\frac{\theta}{3}+120^\circ k)\right),~k=0,1,2$$
最後只需計算 $$\sqrt[3]{r}$$ 及 $$\theta/3$$,再由三角函數值表查出 $$\cos\frac{\theta}{3}$$, $$\sin \frac{\theta}{3}$$ 的值,即可得到此三方根。
由上述過程可以發現解方根的過程中,查表占了很重要的地位,除了最後的查表,一開始的幅角 $$\theta$$,也必須查正切值表得知。解根過程中的查表可由以下簡略流程表示:
$$\tan\theta=\frac{y}{x}\longrightarrow$$ 反查表得 $$\theta\longrightarrow \frac{\theta}{3}\longrightarrow$$ 查表得 $$\cos\frac{\theta}{3}$$、$$\sin\frac{\theta}{3}$$
過程中有查表也有反查表,感覺上繞了點路,難道不能想辦法略過中間的查表嗎?即若已知 $$\tan\theta$$ 的值,如何不查表直接推得 $$\theta/3$$ 的三角函數值?
棣美弗針對此問題的回答是:「沒有正弦值表的幫忙,這件事(解方程式)根本不可能完成。」
利用恆等式躲避查表?
且不管棣美弗的意見為何,讓我們試試看,比方說若已知 $$\tan\theta$$ 的值,若想利用三角恆等式直接推得 $$\tan\frac{\theta}{3}$$,首先想到三倍角公式
$$\displaystyle\tan 3\theta=\frac{3\tan\theta-\tan^3\theta}{1-3\tan^2\theta}$$
,將之改寫成
$$\displaystyle\tan \theta=\frac{3\tan\frac{\theta}{3}-\tan^3\frac{\theta}{3}}{1-3\tan^2\frac{\theta}{3}}$$
不難看出則其為 $$\tan\frac{\theta}{3}$$ 的「三次」方程式;故若想得知 $$\tan\frac{\theta}{3}$$,必須解一元實係數三次方程式,與求方根相比,其困難程度似乎有增無減,唯現在我們只關心其「實數」解。
解三次方程式有個利器——卡當公式,任何三次方程式 $$ax^{3}+bx^{2}+cx+d=0$$ 都可經由變數代換消去二次項,而卡當公式即是針對形如 $$x^{3}+px+q=0$$ 的方程式,要利用卡當公式計算方程式的解,必須先計算以下兩項
$$\displaystyle\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$$、$$\displaystyle\sqrt[3]{\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$$
只要 $$27q^{2}+4p^{3}<0$$,則立方根號裡的虛部便不為零,問題又跳回求複數的三次方根!
將上述流程簡化如下
不藉由 $$\tan\theta$$,想改用正弦或餘弦又如何呢?因為正弦、餘弦的三倍角公式為
$$\displaystyle \sin\theta=3\sin\frac{\theta}{3}-4\sin^3\frac{\theta}{3},~\cos\theta=4\cos^3\frac{\theta}{3}-3\cos\frac{\theta}{3}$$
過程中會碰到實係數三次方程式,故結果也是一樣的。
實例說明
以 $$81+30\sqrt{3}i$$ 的三次方根為例,要找 $$z=x+yi=81+30\sqrt{3}i$$ 的三次方根,先求出此複數的絕對值及幅角的三角函數值:
$$\displaystyle r=21\sqrt{21},~~\tan\theta=\frac{10\sqrt{3}}{27}$$
利用 $$\tan\theta =\frac{10\sqrt{3}}{27} $$,欲求 $$\frac{\theta}{3}$$ 的三角函數值 $$\cdots(1)$$
而 $$\displaystyle\cos\theta=\frac{x}{r}=\frac{81}{21\sqrt{21}}=\frac{9\sqrt{21}}{49}$$
利用三倍角公式 $$\displaystyle\cos\theta=4\cos^3\frac{\theta}{3}-3\cos\frac{\theta}{3}$$
將問題轉換成解三次方程式 $$\frac{9\sqrt{21}}{49}=4x^{3}-3x$$,
移項整理得 $$196x^{3}-147x-9\sqrt{21}=0$$
利用卡當公式,將 $$p=-\frac{3}{4}$$,$$q=\frac{9\sqrt{21}}{196}$$ 代入,化簡後可得
$$\displaystyle\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$$、$$\displaystyle\sqrt[3]{\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$$
$$\displaystyle=\frac{1}{14}\sqrt[3]{-63\sqrt{21}\pm 70\sqrt{7}i}$$
於是我們需要找 $$-63\sqrt{21}\pm 70\sqrt{7}i $$的三次方根(又是複數的三次方根!),先將之化為極式,其絕對值
$$r=\sqrt{(-63\sqrt{21})^2+(70\sqrt{7})^2}=343$$
且幅角的正切值 $$\displaystyle \tan\theta=\frac{\pm 70\sqrt{7}}{-63\sqrt{21}}=\frac{\mp 10\sqrt{3}}{27}$$
已知 $$\displaystyle \tan\theta=\frac{\mp 10\sqrt{3}}{27}$$,想找 $$\displaystyle\frac{\theta}{3}$$ 的三角函數值 $$\cdots(2)$$
注意到 $$(1)$$、$$(2)$$ 幾乎一模一樣,我們又回到了原點!
當年為了說服他人三角函數值表的必要性,棣美弗提出此巧例,他說:「任何想繞過三角函數值表求出方根的辦法,最後都會回到原來的問題。」換作其他例子,$$(1)$$、$$(2)$$ 式不必然雷同,不過可以肯定的是,我們會不斷需要解複數的方根。
然而棣美弗舉錯例子了!因為透過巧妙的變數代換 $$196x^{3}-147x-9\sqrt{21}=0$$ 可以避免使用卡當公式,也就是能不再落入複數方根的輪迴,換句話說,$$81+30\sqrt{3}i$$ 的三次方根可以不透過三角函數值表解出來[註]!
參考資料
- 毛起來說三角,毛爾,天下。


 前一篇文章
前一篇文章 下一篇文章
下一篇文章
