Z-檢定、t-檢定

Z-檢定、t-檢定 (Z-test,Student’s t-test)
國立臺灣大學農藝學系 黃纕淇

一、前言

假設今天我們獲得一筆隨機樣本資料，且此樣本取自於未知來源的族群，該如何判斷此樣本是否來自於某一特定的族群？我們通常會用平均值和變異數來表示某一族群的特性，而本篇主要介紹樣本資料是否來自於某一特定平均值族群的檢定，在此會介紹當族群標準差 \(\sigma\) 已知的\(Z\)-檢定及當族群標準差 \(\sigma\) 未知的\(t\)-檢定。

二、Z-檢定 (Z-test)

\(Z\)-檢定是應用在抽得樣本的族群平均數未知、但此族群標準差已知為 \(\sigma\) 的情況，藉由比較樣本平均值 \(\overline{y}\) 與預先設定好的族群平均值 \(\mu_0\)，來判斷此隨機樣本是否抽取自族群平均值為 \(\mu_0\) 的常態分布。計算樣本平均值之標準化值 \(Z\) 過程為：

\(\displaystyle Z=\frac{|\overline{y}-\mu_0|}{\sigma/\sqrt{n}}~~~~~~~~~(1)\)

(1) 式中的 \(\overline{y}\) 為此組隨機樣本平均值，\(\mu_0\) 為虛無假設預設的平均值，\(\sigma\) 族群已知的標準差，\(n\) 則是抽樣的樣本數。例如，欲檢定某一大豆品種每公頃的平均產量是否等於 \(\mu_0= 1500\) 公斤，研究人員由栽種此品種大豆的田地中，隨機取樣 \(n=36\) 塊面積為一公頃的田地，分別記錄此大豆品種的產量，並計算出這筆隨機樣本平均產量 \(\overline{y}\) 為 \(1520\) 公斤，而研究者在事前已知族群標準差 \(\sigma\) 為 \(350\) 公斤，則計算出來的

\(\displaystyle Z=\frac{|\overline{y}-\mu_0|}{\sigma/\sqrt{n}}=\frac{1520-1500}{350/\sqrt{36}}=0.34\)

\(20\) 公斤的差異 (或 \(Z = 0.34\)) 夠不夠大？我們可以指定一個合理的臨界值，如果差異小於這個臨界值，我們就認定此樣本就來自平均值為 \(\mu_0\) 的族群。這個臨界值我們通常設為 \(Z_{0.025}=1.96\)，這個數字是標準常態分布的 \(97.5\%\) 百分位數。在大豆平均產量的範例中，由於 \(Z < 1.96\)，表示此大豆品種的族群平均產量與 \(1500\) 公斤無顯著差異，而樣本平均值 \(1520\) 公斤略高於 \(1500\) 公斤，單純是抽樣誤差造成的結果。

三、t-檢定 (Student’s t-test)

\(Z\)-檢定的概念可延伸至\(t\)-檢定，而\(t\)-檢定是應用在抽得樣本的族群平均數未知、族群標準差也未知的情況。然而在介紹\(t\)-檢定之前，就先讓我們探究其名稱的由來。

二十世紀初，位於愛爾蘭都柏林的Guinness釀酒公司為了開發新的釀酒科學技術，雇用一群牛津大學和劍橋大學畢業的化學家，包含擁有牛津化學和數學雙學位的W.S. Gosset。Gosset發揮其在管理上的長才，但是他對於釀酒公司最大的貢獻卻是來自統計研究。由於當時公司的政策是為避免商業機密公開，不准員工對外發表文章，Gosset藉由好友Karl Pearson擔任當時<生物統計>期刊的主編的機緣，決定以Student的筆名發表其研究成果，其後三十年，Student寫了一系列極重要的論文，幾乎都發表在<生物統計>上，\(t\)-檢定就是其中之一，而Guinness公司始終不知道Student的真實身分，直到1937年Gosset意外死於心臟病後，數學界好友群聚在Guinness公司，想集資為其論文出專書，公司才得知此消息。

假設 \(n\) 個觀測值抽自同一常態族群，且此常態族群平均值 \(\mu\) 與族群標準差 \(\sigma\) 均未知，(1) 式的 \(Z\) 值將無法計算，替代方案是以樣本標準差 \(s\) 取代未知的族群標準差 \(\sigma\)，得以下 \(t\) 值公式:

\(\displaystyle t=\frac{|\overline{y}-\mu_0|}{s/\sqrt{n}}~~~~~~~~~(2)\)

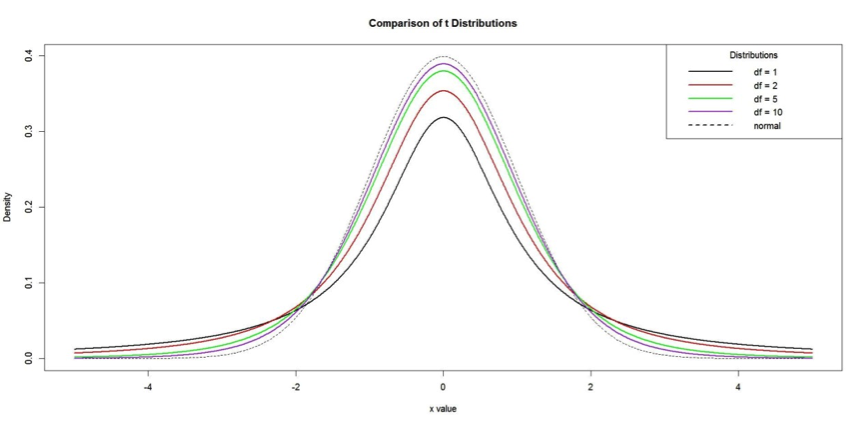
\(t\) 值服從自由度為 \(n-1\) 的 \(t\) 分布。\(t\) 分布為對稱於 \(0\) 的鐘型分布，但其尾部較標準常態分布厚，即變異比標準常態分布大，隨著自由度增大，\(t\) 分布會逐漸趨向於標準常態分布（圖一）。

圖一 t分布的圖，可發現當自由度越大時，t分布兩側會越來越薄，而且越來越近似標準常態分布。

\(t\)-檢定與\(Z\)-檢定相仿，藉由比較樣本平均值 \(\overline{y}\) 與預先設定好的族群平均值 \(\mu_0\)，來判斷此隨機樣本是否抽取自族群平均值為 \(\mu_0\)的常態分布。若 (2) 式的 \(t\) 統計量小於指定的臨界值，我們就認定此樣本就來自平均值為 \(\mu_0\) 的族群；\(t\) 檢定的臨界值我們通常設為 \(t_{0.025,n-1}=\) 自由度為 \(n-1\) 的 \(t\) 分布的 \(97.5\%\) 百分位數，該數值可以利用 Excel 的T.INV函式取得。

假設研究者獲得一筆樣本數為 \(10\)，其樣本平均值 \(\overline{y}\) 為 \(41\) 以及樣本標準差 \(s\) 為 \(3.59\) 的資料，代入 (2) 式得

\(\displaystyle t=\frac{|\overline{y}-\mu_0|}{s/\sqrt{n}}=\frac{|41-42|}{3.59/\sqrt{10}}=0.88\)

由於此筆資料的樣本數為 \(10\)，因此計算出來的 \(t\) 值自由度為 \(9\)，以Excel函式 \(\mathrm{T.INV}(0.975, 9)\) 可得\(t_{0.025,n-1}=2.262\)，由於 \(t\) 值 \(= 0.88 < 2.262\)，表示抽取此樣本之族群的平均值與 \(42\) 無顯著差異。

參考文獻

1. 沈明來 (2014)。生物統計學入門第六版。九州出版社。台北。
2. 歐尚靈。生物統計學課堂ppt。中興大學。台中。