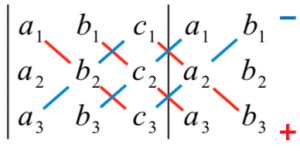行列式的定義
行列式的定義 (Definitions of Determinant)
國立臺南第一高級中學林倉億老師
在高中數學課本中,對於二階與三階行列式,基本上都是直接給出操作型定義:
定義1:\(\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{b_{1}}}\\ {{a_{2}}}&{{b_{2}}} \end{array}} \right| = {a_{1}}{b_{2}} – {a_{2}}{b_{1}}\)。
等號的左邊稱為二階行列式,等號的右邊稱為二階行列式的展開式,或稱為二階行列式的值。
定義2:\(\left| {\begin{array}{*{20}{c}} {{a_{1}}}&{{b_{1}}}&{{c_{1}}}\\ {{a_{2}}}&{{b_{2}}}&{{c_{2}}}\\ {{a_{3}}}&{{b_{3}}}&{{c_{3}}} \end{array}} \right| = {a_{1}}{b_{2}}{c_{3}} + {a_{2}}{b_{3}}{c_{1}} + {a_{3}}{b_{1}}{c_{2}} – {a_{3}}{b_{2}}{c_{1}} – {a_{2}}{b_{1}}{c_{3}} – {a_{1}}{b_{3}}{c_{2}}\)
等號的左邊稱為三階行列式,等號的右邊稱為三階行列式的展開式,或稱為三階行列式的值。
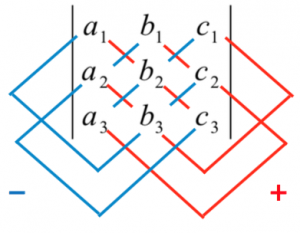
然後再根據定義推導相關的運算性質,最後再介紹它們的應用。定義二其實很難記憶,因此一般教科書都會補充記憶的方法,就是將圖一或圖二中,紅線上的數乘積之和,減去藍線上的數乘積之和。