數學
數學之旅:三角形面積公式(I)
數學之旅:三角形面積公式(I)
(Mathematical Journey through the Formulas of Triangle Area)
國立蘭陽女中陳敏晧教師
三角形面積公式是數學中面最常用的公式,也是大家在小學學數學的甜蜜記憶。
希臘哲人柏拉圖曾說:「畫在沙地上的三角形可以被抹去,但是,三角形的觀念不會受時間與空間的限制而留存下來。」可見三角形的觀念與發展會隨著人類數學發展而不斷變化。但是,不論如何演變,數學的新論點卻永遠根植於舊有的基礎上。
從個人學習數學的歷程看來,三角形的面積公式就如同是典範(paradigm)般的重要。我們可以透過公式的演變來重新釐清學習的轉移(shift);當吾人從數學史的知識論脈絡切入,會發現三角形的面積公式從幾何學出發,邁向三角學領域,接引向量,拓展行列式,認識內積與外積,於解析幾何處發揚光大。
過圓上一點求切線(二) (Finding the tangent line through a point on a circle Ⅱ)
過圓上一點求切線(二)(Finding the tangent line through a point on a circle Ⅱ)
國立臺灣師範大學數學所博士班黃俊瑋
連結:過圓上一點求切線(一)
前文〈過圓上一點求切線(一)〉裡,介紹了此問題的公式解以及另外兩類求切線方法。本文繼續介紹其它方法,其中包含了兩種與微分相關的方法。在此先重述一次原問題:
已知坐標平面上一圓之方程式為 \({(x – 1)^2} + {(y – 2)^2} = 5\),
求過此圓上一點 \(P(3,1)\) 的切線方程式。
方法3圓心到切線距離等於半徑
先利用點斜式可假設過 \(P(3,1)\) 之切線方程式為:\(y-1=m(x-3)\)。
又如圖一所示,圓心到切線距離等於圓之半徑(\(d(O,L) = r\)),利用此關係以及點到直線距離公式可得:
\(\displaystyle\frac{{|m – 2 – 3m + 1|}}{{\sqrt {{m^2} + 1} }} = \sqrt 5\)
此時,兩邊平方並進一步整理解之得 \(m=2\)。則所求切線為 \(y-1=2(x-3)\)。
過圓上一點求切線(一) (Finding the tangent line through a point on a circle Ⅰ)
過圓上一點求切線(一)(Finding the tangent line through a point on a circle Ⅰ)
國立臺灣師範大學數學所博士班黃俊瑋
高二上圓與直線相關單元裡,除了介紹平面上的圓與直線的方程式之外,也進一步利用方程式討論了圓與直線的關係。其中,當直線與圓相切時,又衍生出三類常見求切線問題:1.過圓上一點求切線、2.過圓外一點求切線,以及3.求已知斜率之切線。
本文主要聚焦在第一類過圓上一點求切線問題上,一方面提供多類解法,並說明該解法能否推廣用於其它兩類問題,以及能否推廣至拋物線、橢圓與雙曲線相關求切線問題上(現今高中課程有關三類圓錐曲線的求切線問題已刪除,因此,這部份筆者僅略述之)。
如何過圖形上一點求切線方程式(2)(Finding an equation of the tangent line to the curve at the given point(2))
如何過圖形上一點求切線方程式(2)
(Finding an equation of the tangent line to the curve at the given point(2))
臺北市立第一女子高級中學蘇俊鴻老師
接續〈如何過圖形上一點求切線方程式(1)〉最後提出的問題,本文的目的就是介紹微積分如何解決這些難題。首先,我們必須澄清什麼是切線?不能再像過去訴諸圖形直觀,需要對「切線」這個概念賦予明確的定義。我們想要在圖形上一點找到它的切線,因難之處在於我們需要相異兩點才能決定直線,如何能用「切點」定義呢?當然,微積分為我們解決這個困難。
切線的定義
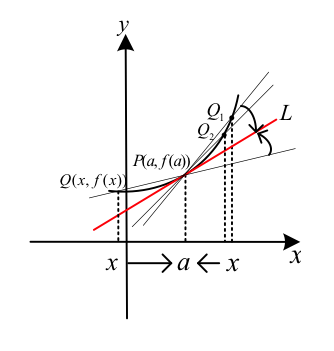
如圖一,設 \(f(x)\) 為一函數,\(P(a,f(a))\) 是 \(y=f(x)\) 圖形上一定點。
在 \(P\) 點附近找圖形上異於 \(P\) 的一點 \(Q(x,f(x))\),連接 \(P,Q\) 可得一割線 \(PQ\)。
當 \(Q\) 點沿著圖形以 \(Q_1,Q_2,\cdots\) 向 \(P\) 點趨近時,能得到一連串的割線 \(PQ_1,PQ_2,\cdots\)。
若 \(Q_n\) 沿著圖形趨近 \(P\) 時,割線 \(PQ_n\) 的極限直線 \(L\) 存在﹐
則稱直線 \(L\) 為 \(y=f(x)\) 圖形上過 \(P\) 點的切線﹐並稱 \(P\) 為切點。也就是說,
割線 \(PQ\xrightarrow{Q\rightarrow P}\)過 \(P\) 點的切線
如何過圖形上一點求切線方程式(1)(Finding an equation of the tangent line to the curve at the given point(1))
如何過圖形上一點求切線方程式(1)
(Finding an equation of the tangent line to the curve at the given point(1))
臺北市立第一女子高級中學蘇俊鴻老師
給定一條曲線圖形(通常可視為函數圖形的一部份),如何求出過圖形上一點的切線方程式?切線問題有著實際應用的對應。例如,運動物體在任意瞬間的運動方向,就是運動軌跡在那一點的切線方向。或是光學透鏡設計需要求出曲面的法線,而法線與切線垂直;若能求出切線,也就決定法線。
這些都是十七世紀當時科學研究和應用的一部份,這些需求促動微積分技術的發展,經過眾人的改進與演化,補強技術的理論,最終發展出微積分這一門優美又有威力的學問。靜心想想,討論「求切線方程式」問題一直是高中數學的主題之一,其解決方法的流變,頗有顯現此種數學知識積累的過程。因此,本文特意將高中數學中相關題材蒐集討論,以饗讀者。
牛頓插值多項式 (3)
牛頓插值多項式 (3) (Newton Interpolating polynomial)
臺北市立第一女子高級中學蘇俊鴻老師
連結:牛頓插值多項式(2)
在〈牛頓插值多項式(2)〉中,我們討論了牛頓插值多項式形式的意義。接下來,我們想要介紹數值分析中對於牛頓插值多項式中各項係數的運算規則和簡便求法。基本上,它的思路和〈牛頓插值多項式(2)〉中所談論的想法一致,只是我們透過符號的輔助,幫助掌握其中所涉及的規律。我們的問題為
給定 \(n+1\) 個資料點 \(({x_0},f({x_0})),({x_1},f({x_1})),({x_2},f({x_2})), \cdots ,({x_n},f({x_n}))\),
求滿足這 \(n+1\) 個資料點的 \(n\) 次多項式 \(f(x)\)。
首先,從滿足兩個點 \(({x_0},f({x_0})),({x_1},f({x_1}))\) 的一次多項式 \(f_1(x)\) 討論起。
假設 \({f_1}(x) = f({x_0}) + {b_1}(x – {x_0})\)
那麼,\({f_1}({x_1}) = f({x_1}) = f({x_0}) + {b_0}({x_1} – {x_0}) \Rightarrow {b_1} = \frac{{f({x_1}) – f({x_0})}}{{{x_1} – {x_0}}}\)。
因此 \({f_1}(x) = f({x_0}) + \frac{{f({x_1}) – f({x_0})}}{{{x_1} – {x_0}}}(x – {x_0})\)
接著,考慮滿足三個點 \(({x_0},f({x_0})),({x_1},f({x_1})),({x_2},f({x_2}))\) 的二次多項式 \(f_2(x)\)。
承上面的結果,可以假設
\(\begin{array}{ll}{f_2}(x) &= {f_1}(x) + {b_2}(x – {x_0})(x – {x_1}) \\&= f({x_0}) + \frac{{f({x_1}) – f({x_0})}}{{{x_1} – {x_0}}}(x – {x_0}) + {b_2}(x – {x_0})(x – {x_1})\end{array}\)
牛頓插值多項式 (2)
牛頓插值多項式 (2) (Newton Interpolating polynomial)
臺北市立第一女子高級中學蘇俊鴻老師
連結:牛頓插值多項式(1)
一樣從這個問題開始
給定平面上三點 \(A(1,7)\),\(B(2,6)\) ,\(C(3,11)\),求圖形通過這三點的二次多項式。
我們知道基於牛頓插值多項式,可以假設所求函數 \(f(x)\)為
\(f(x) = f(1) + a(x – 1) + b(x – 1)(x – 2)\)
通常開頭這個形式就是初學者亟需跨越的門檻。本文試圖利用學生已經擁有的多項式知識,提供一個教學上可行的引導,尚請方家不吝指教。至於學生需要知道什麼多項式的知識呢?只要因式定理即可。
牛頓插值多項式 (1)
牛頓插值多項式 (1) (Newton Interpolating polynomial)
臺北市立第一女子高級中學蘇俊鴻老師
由於多項式「常被用來逼近一般函數,並用來求一般函數的近似值。」,使得插值多項式有了學習的正當性,99課綱並特意引進拉格朗日插值多項式。
例如:以給定平面上三點 \(A(1,7),B(2,6),C(3,11)\) 為例,求圖形通過這三點的二次多項式。上述的問題等同於求一個二次多項函數 \(f(x)\),使得 \(f(1)=7,f(2)=6,f(3)=11\)。
那麼,滿足條件的拉格朗日插值多項式為
\(\displaystyle f(x) = 7 \cdot \frac{{(x – 2)(x – 3)}}{{(1 – 2)(1 – 3)}} + 6 \cdot \frac{{(x – 1)(x – 3)}}{{(2 – 1)(2 – 3)}} + 11 \cdot \frac{{(x – 1)(x – 2)}}{{(3 – 1)(3 – 2)}}\)。
然而,許多課本還加碼補充牛頓插值多項式的方法(這也說明有著各種不同形式的插值多項式)。
通常開頭就會寫道:假設基於牛頓插值多項式,
滿足條件之函數 \(f(x)=f(1)+a(x-1)+b(x-1)(x-2)\),
再將 \(f(2)=6,f(3)=11\) 代入,求出 \(a,b\)。
事實上,這樣的補充留下的問題,比它所解決的問題還多。例如,為何牛頓插值多項式會是上述的形式?除了背誦記憶規則外,有沒有理解它的其他方法?牛頓插值多項式的假設仍需要再求解未知數,會比拉格朗日插值多項式便利嗎?這個方法最早是牛頓給出的嗎?他如何想到的?是為了解決什麼問題呢?這個系列文章就是想要解答以上這些問題。首先,就由牛頓開始吧!
橢圓平行弦中點共線問題 (Collinearity Problem on the Midpoints of Parallel Chords of an Ellipse)
橢圓平行弦中點共線問題
(Collinearity Problem on the Midpoints of Parallel Chords of an Ellipse)
臺北市立和平高中黃俊瑋教師
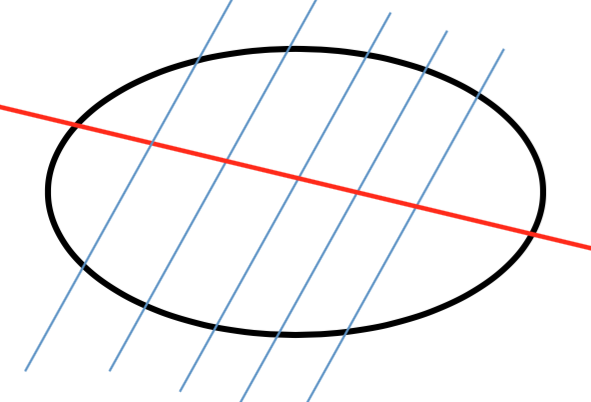
高中圓錐曲線單元裡,一個常見的延伸問題如下:在橢圓 \(\Gamma :\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) 內所有斜率為 \(2\) 的平行弦,已知這些弦的中點共線,請問其所在直線方程式為何(參見圖一)?
換言之,本問題相當於:已知直線 \(y = 2x + k\) 與 \(\Gamma :\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) 相截於兩點 \(A,B\),當參數 \(k\) 變動時,求 \(A\) 與 \(B\) 之中點 \(M(x,y)\) 的軌跡所在直線方程式。