複利(Compound interest)

Posted on 2010/12/01 in 函數, 指數與對數函數, 數學 with 尚無留言 7,267 views

複利(Compound interest)
國立北門農工職業學校數學科李建宗老師/國立台灣師範大學數學系洪萬生教授責任編輯

錢滾錢的方式，可能讓人富有也可能讓有債務的人破產，那麼，錢如何滾錢呢？當然就財務上所謂複利的效果，也就是假設你有 $$100$$ 萬元年初存入銀行，銀行給你一年 $$2\%$$ 的利息，如果每一年計息一次，則一年後你銀行存款就會有 $$100\times(1+0.02)=102$$ 萬，隔年如果繼續存款，那原本利息就會加入本金，也就是說新的一年度，你的本金就會變成 $$102$$萬，第二年末的本利和就為 $$102\times(1+0.02)= 100\times(1+0.02)^2$$ 萬，如果繼續存了 $$5$$ 年都未領出任何錢，則五年後你的銀行存款會有 $$100\times(1+0.02)^5$$，我們利用圖（一）來表示這種情況。

像這種每年利息加入隔年本金計息的方式，我們就稱為複利，而如果現在有本金 $$P_0$$，年利率定為 $$r(100\%)$$，則 $$t$$ 年後本利和就為 $$P_0{(1+r)}^t$$，複利效果也就是等比級數的呈現。

現實生活中，計息週期的方式可能是以年、半年、季、月、半月、周和日計息，不同週期的計息方式，會得到不同的利息錢，而從直觀上，似乎計息的週期越短，錢滾錢效果好像越好，利息越多，真如直觀上的想法嗎？讓我們來驗證看看。

首先，假設一年計息的次數共 $$n$$ 期，即由圖（一）將每一年分割成 $$n$$ 等分且每一等分的利率就會變成 $$\frac{r}{n}$$，$$t$$ 年就會變成 $$nt$$ 期，所以，$$t$$ 年後本利和就更為 $$P_0(1+\frac{r}{n})^{nt}$$。

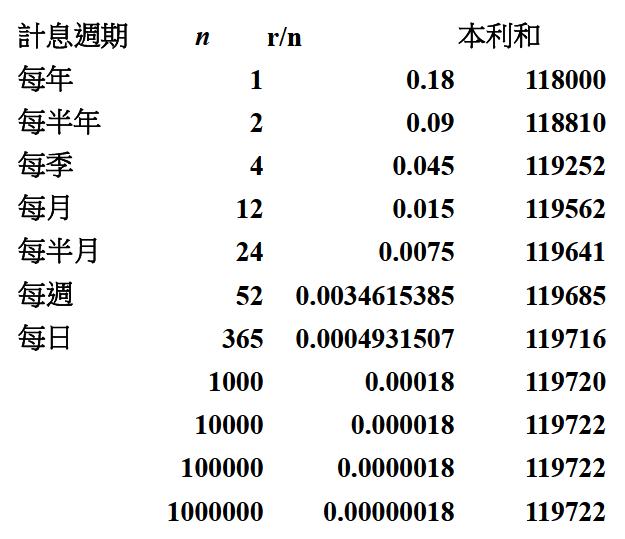
假設某人借了現金卡 $$10$$ 萬元，年利率 $$18\%$$，在一年內都未還任何款項下，那讓我們來看當分別以年、半年、季、月、半月、週、和日計息時，一年後所需還錢會是多少？也就是當 $$P_0=10$$ 萬、$$r=18\%$$、$$t=1$$，$$n$$ 不同情況的本利和會是多少？由表（一）發現本利和隨著期數增加，會逐漸增加，所以和我們直觀想法是一樣。

隨著期數越增越多至無限制時，又會如何呢？這樣本利和增加會有界限嗎？由表（一），我們可以初步發現似乎在不考慮小數位數下，到一定值會穩定，並不會無限制增加。當然，如果想得到更精密結果，可能需要藉由數學嚴謹分析與證明，才可以得知該數列是否確實穩定下來，而不會再增加。利用微積分的語言，我們就可以證明該數列是會收斂到某一個數值。

表（一）當 $$P_0=10$$ 萬、$$r=18\%$$、$$t=1$$，不同利息週期下，一年後本利和

既然收斂一詞出現，就得套用為積分的語言，那麼，極限 $$\displaystyle\lim_{n\to\infty}P_0(1+\frac{r}{n})^{nt}$$ 會收斂於怎樣一個數？如果我們假設 $$P_0=1$$、$$r=1$$ 且 $$t=1$$，則複利公式就改成 $$\displaystyle\lim_{n\to\infty}(1+\frac{1}{n})^{n}$$，而這個式子在數學上就稱為 $$e$$，也就是歐拉數（Euler’s number），如果模擬表（一）的方法，就可以發現 $$e$$ 大約等於 $$2.71828\mbox{…}$$，而 $$\displaystyle\lim_{n\to\infty}P_0(1+\frac{r}{n})^{nt}$$ 就會等於 $$P_0e^{rt}$$，取以 $$e$$ 為底的對數為 $$\log_e$$，又可以寫成 $$\ln$$，稱為自然對數。

原本看似不相關的複利公式與歐拉數，在極限的無窮威力下，卻變成了密不可分，這或許又是數學充滿無限想像的展現吧。

參考文獻：