泰勒多項式(1) (Taylor Polynomials(1))
泰勒多項式(1) (Taylor Polynomials(1))
臺北市立第一女子高級中學蘇俊鴻老師
請考慮下面的問題:
已知多項式函數 \(f(x)=-x^3+5x^2-8x+4\),求 \(f(0.99)\) 的值(四捨五入取到小數點以下第二位)。
儘管將 \(x=0.99\) 代入,即可求出函數值。
但 \(f(0.99) =- {(0.99)^3} + 5 \times {(0.99)^2} – 8 \times (0.99) + 4\) 繁複計算過程令人卻步。
因此,處理這類問題,通常採取下面的作法
- 步驟一:將 \(f(x)\) 表示成 \(f(x) = a + b(x – 1) + c{(x – 1)^2} + d{(x – 1)^3}\),
計算出 \(a,b,c,d\) 各值。此題的結果 \(a=0,b=-1,c=2,d=-1\) - 步驟二:將 \(x=0.99\) 代入,即可估取近似值。
以上題為例,由步驟一知,\(f(x) =- (x – 1) + 2{(x – 1)^2} – {(x – 1)^3}\)。所以,
\(\begin{array}{ll} f(0.99) &=-(0.99-1)+2\times{(0.99-1)^2}-{(1-0.99)^3}\\&=-(0.01)+2\times{(0.01)^2}-{(0.01)^3}\\&\approx -(0.01)=-0.01\end{array}\)
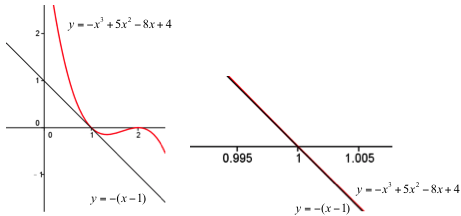
由步驟二的數值計算來看,應能推敲步驟一將原多項式改寫成以 \((x-1)\) 的冪次方升冪排列的多項式之用意。不過,進一步思考,上述解法正表明:當 \(1-\varepsilon\le x\le 1+\varepsilon\),其中的 \(\varepsilon\) 為足夠小的正數時,有 \(f(x)\approx -(x-1)\)。
換言之,三次函數 \(f(x)\) 在 \(x=1\) 附近的局部圖形幾乎就是 \(y=-(x-1)=1-x\) 的一次函數(見圖一)。更進一步的討論和說明,請參閱本網站中單維彰教授所寫〈多項式函數圖形的巨觀與微觀〉一文。
事實上,形如 \(f(x) =- (x – 1) + 2{(x – 1)^2} – {(x – 1)^3}\) 的多項式,被稱為以 \(x=1\) 為參考點的泰勒多項式(Taylor Polynomials)。這是為了紀念英國數學家布魯克.泰勒(Brook Taylor, 1685-1731)在1712年對於泰勒定理(Taylor’s theorem)的提出。
然而,在步驟一中留下的問題是:如何決定係數 \(a,b,c,d\) 各值?這也是寫出泰勒多項式的關鍵,以下介紹幾種常見的方法。
方法一 直接將等式兩邊展開,比較係數
\(\begin{array}{l}f(x) = – {x^3} + 5{x^2} – 8x + 4 = a + b(x – 1) + c{(x – 1)^2} + d{(x – 1)^3}\\\Rightarrow – {x^3} + 5{x^2} – 8x + 4 \\~~~~~~= d{x^3} + (c – 3d){x^2} + (b – 2c + 3d)x + (a – b + c – d)\\\Rightarrow \left\{ \begin{array}{l} d = – 1\\ c – 3d = 5\\ b – 2c + 3d = – 8\\ a – b + c – d = 4 \end{array} \right.\Rightarrow \left\{ \begin{array}{l} a = 0\\ b = – 1\\ c = 2\\ d = – 1 \end{array} \right.\end{array}\)
因此,\(a=0,b=-1,c=2,d=-1\)。
方法二 利用綜合除法,如圖二所示。
因此,\(a=0,b=-1,c=2,d=-1\)。
透過對商式的反覆相除,就能求出一系列的係數,原因由下面的式子推導應能看出
上述這兩個方法是高中數學多項式單元中常用的方法,特別是利用綜合除法的作法,更是老師強調的學習重點。
不過,學過微分後,這個問題就有其他的解決方法。
方法三 利用微分處理。
由於
\(f(x) =-{x^3} + 5{x^2} – 8x + 4 = a + b(x – 1) + c{(x – 1)^2} + d{(x – 1)^3}\cdots (1)\),
\(f(1) =-1+5-8+4=a \Rightarrow a = 0\),
\((1)\) 式兩邊微分,\(f'(x) =-3{x^2} + 10x – 8 = b + 2c(x – 1) + 3d{(x – 1)^2}\cdots (2)\),
\(\Rightarrow f'(1)=-3+10-8=b \Rightarrow b=-1\),
\((2)\) 式兩邊微分,\(f”(x) =-6x + 10 = 2c + 6d(x – 1) \cdots (3)\),
\(\Rightarrow f”(1)=-6+10=2c \Rightarrow c=2\),
\((3)\) 式兩邊微分,\(f”'(x) =-6=6d \Rightarrow d=-1\)
因此,\(a=0,b=-1,c=2,d=-1\)
由解法過程來看,方法三和方法二差異不大:反覆微分的程序,代入求值。
然而,透過微分的符號,我們能找到泰勒多項式各項係數的規律,其定理如下
若 \(f(x)\) 為實係數 \(n\) 次多項式,\(a\) 為實數,則
\(\begin{multline*}\displaystyle f(x)= f\left( a \right) + \frac{{f’\left( a \right)}}{{1!}}\left( {x – a} \right) + \frac{{f”\left( a \right)}}{{2!}}{\left( {x – a} \right)^2} + \frac{{f”’\left( a \right)}}{{3!}}{\left( {x – a} \right)^3} \\+\cdots+ \frac{{{f^{\left( n \right)}}\left( a \right)}}{{n!}}{\left( {x – a} \right)^n}\end{multline*}\)
上式稱為 \(f(x)\) 在 \(x=a\) 處的泰勒多項式。
定理的證明與方法三相同,有興趣的讀者不妨動筆試一試。
至於泰勒多項式進一步的應用,請見〈泰勒多項式(2)〉一文。
連結:泰勒多項式(2) (Taylor Polynomials(2))
參考文獻:
- 單維彰〈多項式函數圖形的巨觀與微觀〉
/highscope/?p=35934



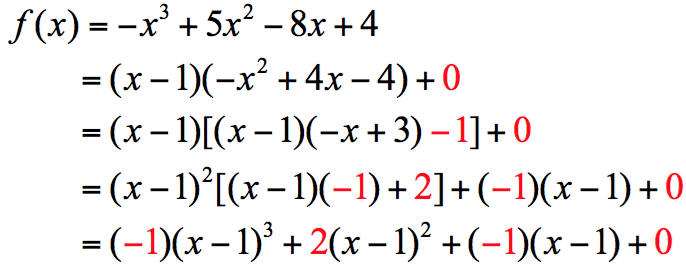
 前一篇文章
前一篇文章 下一篇文章
下一篇文章
