正弦定律 (The Sine Law)

正弦定律 (The Sine Law)
臺北市立第一女子中學數學科蘇俊鴻老師

在現行高中課程中，對於正弦定律的推導常是透過三角形面積公式為媒介：

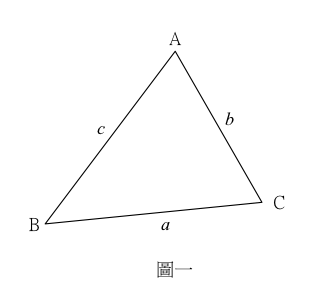
如圖一，給定三角形 \(\Delta ABC\) ，則三角形 \(\Delta ABC\) 的面積為

\(\displaystyle\frac{1}{2}ab\sin C = \frac{1}{2}ac\sin B = \frac{1}{2}bc\sin A\)

因此，\(\displaystyle\frac{{\sin C}}{c} = \frac{{\sin B}}{b} = \frac{{\sin A}}{a} \Rightarrow \frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)

即為正弦定律。也就是 \(a:b:c=\sin A:\sin B:\sin C\)，滿足「大邊對大角，小邊對小角」定量化的描述。儘管這個推導的進路簡單易懂，然而，談到正弦定律，通常還會提到等式的比值為 \(2R\)，其中 \(R\) 為 \(\Delta ABC\) 的外接圓的半徑，即 \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)。

但是，這個比值在上述的推導中是不會出現的。因此，若要適切地引導出這個性質，恐怕得要考慮其他的教學進路。事實上，透過銳角三角函數的幾何表徵(請參閱網站另一篇文章〈銳角三角函數的幾何表徵〉)，是可以圓滿地解決這個問題。

圖二

由於三角函數可以看成角度對應之圓上的某些線段長，不妨考慮銳角 \(\Delta ABC\) 及其外接圓(如圖二)，則 \(\angle A = \theta \)，\(\displaystyle\overline{CH}=\frac{1}{2}a\)。因此，在直角三角形 \(\Delta COH\) 中，

\(\displaystyle\frac{{\frac{1}{2}a}}{R} = \sin \theta= \sin A \Rightarrow \frac{a}{{\sin A}} = 2R\)

同理，\(\displaystyle\frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)。所以，\(\displaystyle\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)。

圖三

至於鈍角三角形的情況，則如圖三。其中，鈍角 \(\angle A = \frac{1}{2}(360^\circ- 2\theta ) = 180^\circ- \theta \)

因此，\(\displaystyle\sin A = \sin (180^\circ- \theta ) = \sin \theta= \frac{{\frac{1}{2}a}}{R} \Rightarrow \frac{a}{{\sin A}} = 2R\)。

若是 \(\angle B,~\angle C\)，只要延長 \(\overline{OB}\) 或 \(\overline{OC}\) 至圓上，再連接 \(A\) 即得圖二的情形。

最後，對於直角三角形，只是特例情形，就請讀者自己動手了。在筆者的課堂上，將上述進路設計成引導式的問題，利用學習單讓學生們分組討論，通常學生都能順利推導出正弦定律，享受自己發現定理的樂趣。